Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 12. Bài viết này sẽ hướng dẫn bạn giải bài 1 trang 20 trong Chuyên đề học tập Toán 12 - Chân trời sáng tạo một cách nhanh chóng và hiệu quả.
Chúng tôi cam kết mang đến cho bạn những giải pháp học tập tốt nhất, giúp bạn nắm vững kiến thức và đạt kết quả cao trong môn Toán.
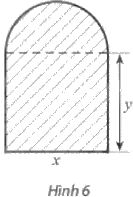
Người ta muốn xây một đường cống thoát nước có mặt cắt ngang là hình tạo bởi một nửa hình tròn ghép với một hình chữ nhật (Hình 6). Biết rằng mặt cắt ngang có diện tích 2 m2. Các kích thước \(x,y\) (đơn vị: m) bằng bao nhiêu để chu vi của mặt cắt ngang là nhỏ nhất? Tính chu vi nhỏ nhất đó.
Đề bài
Người ta muốn xây một đường cống thoát nước có mặt cắt ngang là hình tạo bởi một nửa hình tròn ghép với một hình chữ nhật (Hình 6). Biết rằng mặt cắt ngang có diện tích 2 m2. Các kích thước \(x,y\) (đơn vị: m) bằng bao nhiêu để chu vi của mặt cắt ngang là nhỏ nhất? Tính chu vi nhỏ nhất đó.
Phương pháp giải - Xem chi tiết
• Tìm mối quan hệ giữa \(x,y\), biểu thị chu vi thông qua các đại lượng đã biết và ẩn.
• Cách tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một khoảng hay nửa khoảng bằng đạo hàm:
‒ Lập bảng biến thiên của hàm số trên tập hợp đó.
‒ Căn cứ vào bảng biến thiên, kết luận giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của hàm số.
Lời giải chi tiết
Bán kính nửa hình tròn là \(\frac{x}{2}\).
Diện tích nửa hình tròn là \(\frac{1}{2}\pi .{\left( {\frac{x}{2}} \right)^2} = \frac{{\pi {x^2}}}{8}\).
Diện tích hình chữ nhật là \(xy\).
Diện tích mặt cắt ngang là: \(xy + \frac{{\pi {x^2}}}{8}\).
Do diện tích mặt cắt ngang bằng 2m2 nên ta có: \(xy + \frac{{\pi {x^2}}}{8} = 2 \Rightarrow y = \frac{1}{x}\left( {2 - \frac{{\pi {x^2}}}{8}} \right)\).
Do \(x,y > 0\) nên ta có: \(\frac{1}{x}\left( {2 - \frac{{\pi {x^2}}}{8}} \right) > 0 \Leftrightarrow 2 - \frac{{\pi {x^2}}}{8} > 0 \Leftrightarrow \frac{{\pi {x^2}}}{8} < 2 \Leftrightarrow {x^2} < \frac{{16}}{\pi } \Leftrightarrow x < \frac{4}{{\sqrt \pi }}\)
Chu vi của mặt cắt ngang là:
\(P = \frac{1}{2}.2\pi .\frac{x}{2} + x + 2y = \frac{{\pi x}}{2} + x + 2.\frac{1}{x}\left( {2 - \frac{{\pi {x^2}}}{8}} \right) = \left( {1 + \frac{\pi }{4}} \right)x + \frac{4}{x}\) với \(0 < x < \frac{4}{{\sqrt \pi }}\).
Xét hàm số \(P\left( x \right) = \left( {1 + \frac{\pi }{4}} \right)x + \frac{4}{x}\) trên khoảng \(\left( {0;\frac{4}{{\sqrt \pi }}} \right)\).
Ta có: \(P'\left( x \right) = \left( {1 + \frac{\pi }{4}} \right) - \frac{4}{{{x^2}}}\)
\(P'\left( x \right) = 0 \Leftrightarrow \left( {1 + \frac{\pi }{4}} \right) - \frac{4}{{{x^2}}} = 0 \Leftrightarrow {x^2} = \frac{{16}}{{\pi + 4}} \Leftrightarrow x = \frac{4}{{\sqrt {\pi + 4} }}\) hoặc \(x = - \frac{4}{{\sqrt {\pi + 4} }}\) (loại).
Bảng biến thiên của hàm số trên khoảng \(\left( {0;\frac{4}{{\sqrt \pi }}} \right)\):
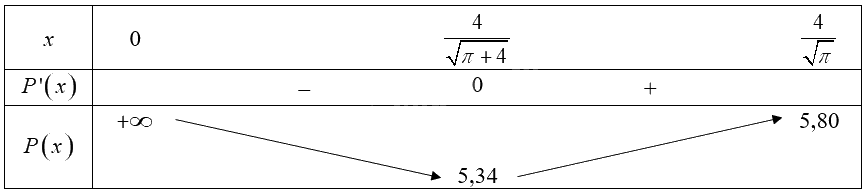
Từ bảng biến thiên, ta thấy \(\mathop {\min }\limits_{\left( {0;\frac{4}{{\sqrt \pi }}} \right)} P\left( x \right) = P\left( {\frac{4}{{\sqrt {\pi + 4} }}} \right) \approx 5,34\).
Vậy chu vi nhỏ nhất của mặt cắt ngang của đường cống là khoảng 5,34 m khi \(x = \frac{4}{{\sqrt {\pi + 4} }} \approx 1,50\left( m \right)\) và \(y = \frac{2}{{\frac{4}{{\sqrt {\pi + 4} }}}} - \frac{{\pi .\frac{4}{{\sqrt {\pi + 4} }}}}{8} \approx 0,75\left( m \right)\).
Bài 1 trang 20 Chuyên đề học tập Toán 12 - Chân trời sáng tạo thuộc chương trình học Toán 12, tập trung vào việc ôn tập và củng cố kiến thức về đạo hàm. Bài tập này yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế, rèn luyện kỹ năng tính toán và tư duy logic.
Bài 1 trang 20 thường bao gồm các dạng bài tập sau:
Để giải bài 1 trang 20 Chuyên đề học tập Toán 12 - Chân trời sáng tạo một cách hiệu quả, bạn cần nắm vững các kiến thức sau:
Dưới đây là lời giải chi tiết cho bài 1 trang 20 Chuyên đề học tập Toán 12 - Chân trời sáng tạo:
Đề bài: Tính đạo hàm của hàm số f(x) = x2 + 2x - 1 tại x = 1.
Lời giải:
f'(x) = 2x + 2
f'(1) = 2(1) + 2 = 4
Vậy, đạo hàm của hàm số f(x) tại x = 1 là 4.
Đề bài: Tìm đạo hàm của hàm số g(x) = sin(x) + cos(x).
Lời giải:
g'(x) = cos(x) - sin(x)
Vậy, đạo hàm của hàm số g(x) là cos(x) - sin(x).
Đề bài: Tìm cực trị của hàm số h(x) = x3 - 3x2 + 2.
Lời giải:
h'(x) = 3x2 - 6x
Giải phương trình h'(x) = 0, ta được x = 0 hoặc x = 2.
h''(x) = 6x - 6
h''(0) = -6 < 0, vậy hàm số đạt cực đại tại x = 0, giá trị cực đại là h(0) = 2.
h''(2) = 6 > 0, vậy hàm số đạt cực tiểu tại x = 2, giá trị cực tiểu là h(2) = -2.
Để học tập và ôn luyện kiến thức về đạo hàm, bạn có thể tham khảo các tài liệu sau:
Bài 1 trang 20 Chuyên đề học tập Toán 12 - Chân trời sáng tạo là một bài tập quan trọng giúp bạn củng cố kiến thức về đạo hàm và rèn luyện kỹ năng giải toán. Hy vọng với lời giải chi tiết và phương pháp giải bài tập được trình bày trong bài viết này, bạn sẽ tự tin hơn khi đối mặt với các bài toán tương tự.