Giải bài 17 trang 52 Chuyên đề học tập Toán 12 - Chân trời sáng tạo

Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 12. Bài viết này sẽ hướng dẫn bạn giải bài 17 trang 52 thuộc Chuyên đề học tập Toán 12 - Chân trời sáng tạo một cách nhanh chóng và hiệu quả.

Chúng tôi cam kết mang đến cho bạn những giải pháp học tập tốt nhất, giúp bạn nắm vững kiến thức và tự tin trong các kỳ thi.

Cho biết thông tin về một số cổ phiếu theo mã và ngành như sau: a) Vào ngày 03/4/2013, bác Hiền đầu tư bằng cách mua 20.000 cổ phiếu ICC với giá mỗi cổ phiếu là 12000 đồng. Đến ngày 03/4/2023, bác Hiển bán hết số cổ phiếu nói trên. Hãy tính tổng số tiền lời mà bác Hiền thu được từ việc cổ phiếu tăng giá và tiền cổ tức được chia hằng năm. b) Vào ngày 03/4/2018, cô Trang đã mua 28000 cổ phiếu PAT với giá mỗi cổ phiếu là 61480 đồng. Đến ngày 03/4/2023, cô Trang bán hết số cổ phiếu nói trên. Hãy

Đề bài

Cho biết thông tin về một số cổ phiếu theo mã và ngành như sau:

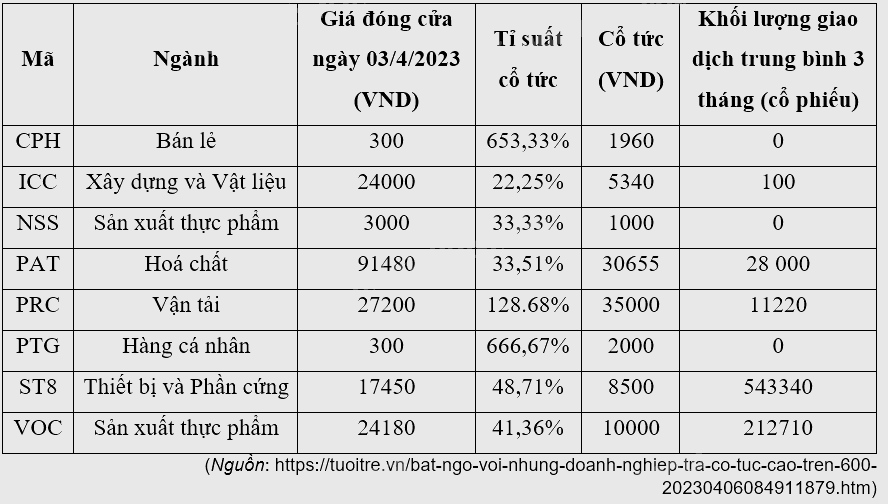Giải bài 17 trang 52 Chuyên đề học tập Toán 12 - Chân trời sáng tạo 1 a) Vào ngày 03/4/2013, bác Hiền đầu tư bằng cách mua 20.000 cổ phiếu ICC với giá mỗi cổ phiếu là 12000 đồng. Đến ngày 03/4/2023, bác Hiển bán hết số cổ phiếu nói trên. Hãy tính tổng số tiền lời mà bác Hiền thu được từ việc cổ phiếu tăng giá và tiền cổ tức được chia hằng năm. b) Vào ngày 03/4/2018, cô Trang đã mua 28000 cổ phiếu PAT với giá mỗi cổ phiếu là 61480 đồng. Đến ngày 03/4/2023, cô Trang bán hết số cổ phiếu nói trên. Hãy tính tổng số tiền lời mà cô Trang thu được từ việc cổ phiếu tăng giá và tiền cổ tức được chia hằng năm.

Phương pháp giải - Xem chi tiết Giải bài 17 trang 52 Chuyên đề học tập Toán 12 - Chân trời sáng tạo 2

‒ Tính số tiền mua cổ phiếu.

‒ Tính số tiền bán cổ phiếu.

‒ Tính số tiền lời từ cổ phiếu tăng giá.

‒ Tính số tiền cổ tức nhận được.

‒ Tính số tiền lời từ cổ phiếu tăng giá và cổ tức nhận được.

Lời giải chi tiết

a) Số tiền mua cổ phiếu ICC là: \(20000.12000 = 240000000\) (đồng).

Số tiền bán cổ phiếu ICC là: \(20000.24000 = 480000000\) (đồng).

Tổng số tiền lời từ việc cổ phiếu tăng giá là: \(480000000 - 240000000 = 240000000\) (đồng).

Vì bác Hiền mua cổ phiếu vào ngày 03/4/2013 và bán vào ngày 03/4/2023, nên số năm nắm giữ cổ phiếu là: \(2023 - 2013 = 10\) (năm).

Tổng số tiền cổ tức nhận được là: \(20000.5340.10 = 1068000000\) (đồng).

Tổng số tiền lời từ việc cổ phiếu tăng giá và cổ tức là:

\(240000000 + 1068000000 = 1308000000\) (đồng).

Vậy tổng số tiền lời mà bác Hiền thu được từ việc đầu tư cổ phiếu ICC là 1 308 000 000 đồng.

b) Số tiền mua cổ phiếu PAT là: \(28000.61480 = 1721440000\) (đồng).

Số tiền bán cổ phiếu PAT là: \(28000.91480 = 2561440000\) (đồng).

Tổng số tiền lời từ việc cổ phiếu tăng giá là: \(2561440000 - 1721440000 = 840000000\) (đồng).

Vì cô Trang mua cổ phiếu vào ngày 03/4/2018 và bán vào ngày 03/4/2023, nên số năm nắm giữ cổ phiếu là: \(2023 - 2018 = 5\) (năm).

Tổng số tiền cổ tức nhận được là: \(28000.30655.5 = 4291700000\) (đồng).

Tổng số tiền lời từ việc cổ phiếu tăng giá và cổ tức là:

\(840000000 + 4291700000 = 5131700000\) (đồng).

Vậy tổng số tiền lời mà cô Trang thu được từ việc đầu tư cổ phiếu PAT là 5 131 700 000 đồng.

Tự tin bứt phá Kỳ thi THPT Quốc gia môn Toán! Đừng bỏ lỡ Giải bài 17 trang 52 Chuyên đề học tập Toán 12 - Chân trời sáng tạo đặc sắc thuộc chuyên mục đề toán 12 trên nền tảng tài liệu toán. Với bộ bài tập lý thuyết toán thpt được biên soạn chuyên sâu, bám sát cấu trúc đề thi và chương trình Toán 12, đây chính là "chiến lược vàng" giúp các em tối ưu hóa ôn luyện. Học sinh sẽ không chỉ làm chủ mọi dạng bài thi mà còn nắm vững chiến thuật làm bài hiệu quả, sẵn sàng tự tin chinh phục điểm cao, vững bước vào đại học mơ ước nhờ phương pháp học trực quan, khoa học và hiệu quả học tập vượt trội!

Giải bài 17 trang 52 Chuyên đề học tập Toán 12 - Chân trời sáng tạo: Tổng quan

Bài 17 trang 52 Chuyên đề học tập Toán 12 - Chân trời sáng tạo thuộc chương trình học Toán 12, tập trung vào việc vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế. Bài tập này thường yêu cầu học sinh phân tích hàm số, tìm cực trị, và khảo sát sự biến thiên của hàm số. Việc nắm vững các khái niệm và kỹ năng liên quan đến đạo hàm là yếu tố then chốt để giải quyết thành công bài toán này.

Phân tích đề bài và xác định yêu cầu

Trước khi bắt đầu giải bài, điều quan trọng là phải đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Trong bài 17 trang 52, học sinh cần xác định hàm số, tìm tập xác định, tính đạo hàm, tìm điểm cực trị, và khảo sát sự biến thiên của hàm số. Ngoài ra, bài toán có thể yêu cầu học sinh vẽ đồ thị hàm số hoặc giải các bài toán liên quan đến ứng dụng của đạo hàm.

Lời giải chi tiết bài 17 trang 52

Để giải bài 17 trang 52, chúng ta sẽ thực hiện các bước sau:

Bước 1: Xác định hàm số: Đề bài sẽ cung cấp một hàm số cụ thể. Ví dụ, hàm số có thể là y = x^3 - 3x^2 + 2.
Bước 2: Tìm tập xác định: Tập xác định của hàm số là tập hợp tất cả các giá trị của x mà hàm số có nghĩa. Trong hầu hết các trường hợp, tập xác định của hàm đa thức là tập số thực R.
Bước 3: Tính đạo hàm: Sử dụng các quy tắc đạo hàm cơ bản để tính đạo hàm cấp một y' của hàm số. Ví dụ, nếu y = x^3 - 3x^2 + 2, thì y' = 3x^2 - 6x.
Bước 4: Tìm điểm cực trị: Giải phương trình y' = 0 để tìm các điểm cực trị của hàm số. Các nghiệm của phương trình này là các giá trị của x tại các điểm cực trị.
Bước 5: Xác định loại điểm cực trị: Sử dụng đạo hàm cấp hai y'' để xác định loại điểm cực trị. Nếu y'' > 0 tại một điểm cực trị, thì đó là điểm cực tiểu. Nếu y'' < 0 tại một điểm cực trị, thì đó là điểm cực đại.
Bước 6: Khảo sát sự biến thiên của hàm số: Dựa vào đạo hàm cấp một và đạo hàm cấp hai, ta có thể khảo sát sự biến thiên của hàm số, bao gồm khoảng đồng biến, khoảng nghịch biến, điểm cực đại, điểm cực tiểu, và giới hạn của hàm số khi x tiến tới vô cùng.
Bước 7: Vẽ đồ thị hàm số: Dựa vào các thông tin đã thu thập được, ta có thể vẽ đồ thị hàm số.

Ví dụ minh họa

Giả sử chúng ta có hàm số y = x^3 - 3x^2 + 2. Chúng ta sẽ áp dụng các bước trên để giải bài toán:

Tập xác định: R
Đạo hàm: y' = 3x^2 - 6x
Điểm cực trị: 3x^2 - 6x = 0 => x = 0 hoặc x = 2
Đạo hàm cấp hai: y'' = 6x - 6
Xác định loại điểm cực trị:
- Tại x = 0: y'' = -6 < 0 => Điểm cực đại
- Tại x = 2: y'' = 6 > 0 => Điểm cực tiểu
Khảo sát sự biến thiên:
- Hàm số đồng biến trên khoảng (-∞, 0) và (2, +∞)
- Hàm số nghịch biến trên khoảng (0, 2)

Lưu ý quan trọng

Khi giải bài 17 trang 52, học sinh cần chú ý các điểm sau:

Đảm bảo tính chính xác của các phép tính đạo hàm.
Phân tích kỹ đề bài để xác định đúng yêu cầu.
Sử dụng các công cụ hỗ trợ như máy tính bỏ túi hoặc phần mềm vẽ đồ thị để kiểm tra kết quả.

Ứng dụng của bài toán

Việc giải bài 17 trang 52 giúp học sinh hiểu rõ hơn về ứng dụng của đạo hàm trong việc phân tích và khảo sát hàm số. Những kiến thức này có vai trò quan trọng trong nhiều lĩnh vực khác nhau, như kinh tế, kỹ thuật, và khoa học tự nhiên.

Tổng kết

Bài 17 trang 52 Chuyên đề học tập Toán 12 - Chân trời sáng tạo là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải quyết các bài toán liên quan đến đạo hàm. Bằng cách thực hiện các bước giải một cách cẩn thận và chính xác, học sinh có thể tự tin giải quyết các bài toán tương tự trong các kỳ thi.