Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 1 trang 54, 55 Chuyên đề học tập Toán 12 - Chân trời sáng tạo. Tại giaitoan.edu.vn, chúng tôi cung cấp các bài giải được trình bày rõ ràng, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải quyết các bài toán.
Chúng tôi hiểu rằng việc học toán đôi khi có thể gặp nhiều khó khăn. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của chúng tôi đã biên soạn các lời giải chi tiết, kèm theo các ví dụ minh họa, giúp các em hiểu sâu sắc về các khái niệm và phương pháp giải toán.
Một hộp chứa 4 tấm thẻ cùng loại được đánh số lần lượt từ 1 đến 4. Lấy ra ngẫu nhiên đồng thời 2 thẻ từ hộp. a) Đại lượng tổng các số viết trên 2 thẻ có thể nhận các giá trị nào? b) Đại lượng tích các số viết trên 2 thẻ có thể nhận các giá trị nào?
Trả lời câu hỏi Luyện tập 2 trang 55 Chuyên đề học tập Toán 12 Chân trời sáng tạo
Một hộp chứa 10 tấm thẻ giống nhau, trong đó có 1 thẻ là thẻ may mắn. Bạn Khuê rút ngẫu nhiên từng thẻ trong hộp cho đến khi lấy được thẻ may mắn. Gọi \(X\) là số thẻ bạn Khuê đã rút cho đến khi lấy được thẻ may mắn. Hỏi \(X\) có phải là biến ngẫu nhiên rời rạc không nếu thẻ đã rút ra không được cho lại vào hộp?
Phương pháp giải:
Sử dụng khái niệm: Biến ngẫu nhiên rời rạc là một đại lượng nhận một số hữu hạn các giá trị bằng số, các giá trị này là ngẫu nhiên và không thể dự đoán trước được.
Lời giải chi tiết:
Do thẻ đã rút không được cho lại vào hộp nên \(X\) nhận giá trị từ 1 đến 10.
Vậy \(X\) là biến ngẫu nhiên rời rạc.
Trả lời câu hỏi Luyện tập 1 trang 55 Chuyên đề học tập Toán 12 Chân trời sáng tạo
Một hộp chứa 5 viên bi xanh và 7 viên bi đỏ có cùng kích thước và khối lượng. Các viên bi xanh được đánh số từ 1 đến 5; các viên bi đỏ được đánh số từ 1 đến 7. Lấy ra ngẫu nhiên cùng một lúc 2 viên bi từ hộp. Trong các đại lượng sau, đại lượng nào là biến ngẫu nhiên rời rạc?
a) Đại lượng \(X\) là tổng các số ghi trên hai viên bi.
b) Đại lượng \(Y\) là tích các số ghi trên hai viên bi.
c) Đại lượng \(Z\) bằng 1 nếu hai viên bi cùng màu, bằng 0 nếu hai viên bi khác màu.
Phương pháp giải:
Sử dụng khái niệm: Biến ngẫu nhiên rời rạc là một đại lượng nhận một số hữu hạn các giá trị bằng số, các giá trị này là ngẫu nhiên và không thể dự đoán trước được.
Lời giải chi tiết:
Đại lượng \(X\) có thể nhận các giá trị từ 2 đến 12.
Đại lượng \(Y\) có thể nhận các giá trị 2, 3, 4, ..., 9, 10, 12, 14, 15, 16, 18, 20, 21, 24, 25, 28, 30, 35.
Đại lượng \(Z\) có thể nhận các giá trị 0 và 1.
Vậy \(X,Y,Z\) đều là các biến ngẫu nhiên rời rạc.
Trả lời câu hỏi Hoạt động 1 trang 54 Chuyên đề học tập Toán 12 Chân trời sáng tạo
Một hộp chứa 4 tấm thẻ cùng loại được đánh số lần lượt từ 1 đến 4. Lấy ra ngẫu nhiên đồng thời 2 thẻ từ hộp.
a) Đại lượng tổng các số viết trên 2 thẻ có thể nhận các giá trị nào?
b) Đại lượng tích các số viết trên 2 thẻ có thể nhận các giá trị nào?
Phương pháp giải:
Liệt kê các giá trị.
Lời giải chi tiết:
a) Ta có:
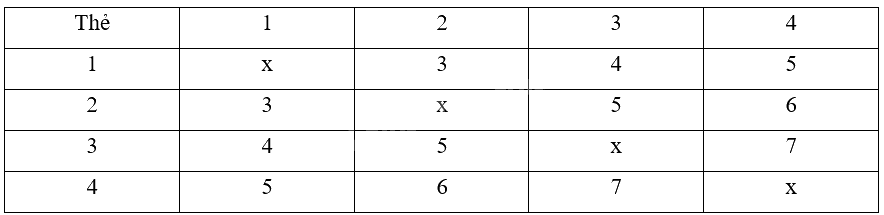
Đại lượng tổng các số viết trên 2 thẻ có thể nhận các giá trị là 3; 4; 5; 6; 7.
b) Ta có:
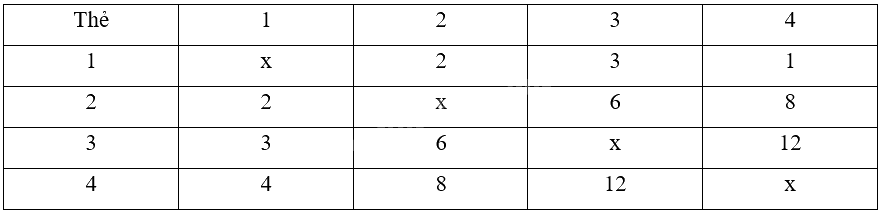
Đại lượng tích các số viết trên 2 thẻ có thể nhận các giá trị là 2; 3; 4; 6; 8; 12.
Trả lời câu hỏi Hoạt động 1 trang 54 Chuyên đề học tập Toán 12 Chân trời sáng tạo
Một hộp chứa 4 tấm thẻ cùng loại được đánh số lần lượt từ 1 đến 4. Lấy ra ngẫu nhiên đồng thời 2 thẻ từ hộp.
a) Đại lượng tổng các số viết trên 2 thẻ có thể nhận các giá trị nào?
b) Đại lượng tích các số viết trên 2 thẻ có thể nhận các giá trị nào?
Phương pháp giải:
Liệt kê các giá trị.
Lời giải chi tiết:
a) Ta có:
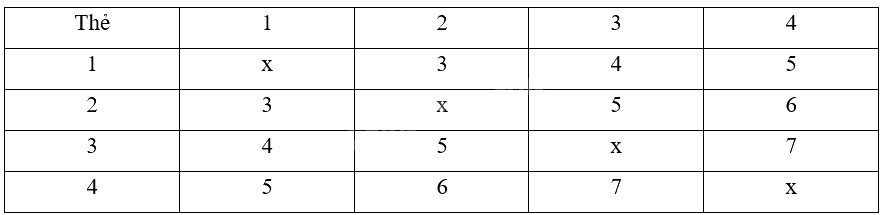
Đại lượng tổng các số viết trên 2 thẻ có thể nhận các giá trị là 3; 4; 5; 6; 7.
b) Ta có:
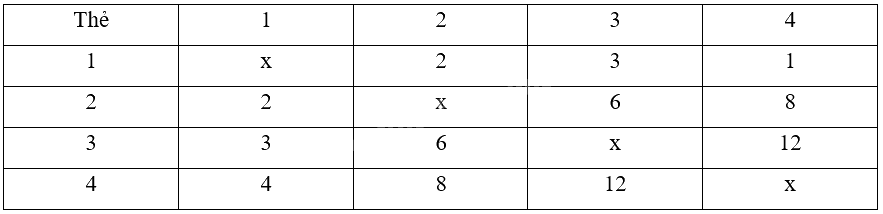
Đại lượng tích các số viết trên 2 thẻ có thể nhận các giá trị là 2; 3; 4; 6; 8; 12.
Trả lời câu hỏi Luyện tập 1 trang 55 Chuyên đề học tập Toán 12 Chân trời sáng tạo
Một hộp chứa 5 viên bi xanh và 7 viên bi đỏ có cùng kích thước và khối lượng. Các viên bi xanh được đánh số từ 1 đến 5; các viên bi đỏ được đánh số từ 1 đến 7. Lấy ra ngẫu nhiên cùng một lúc 2 viên bi từ hộp. Trong các đại lượng sau, đại lượng nào là biến ngẫu nhiên rời rạc?
a) Đại lượng \(X\) là tổng các số ghi trên hai viên bi.
b) Đại lượng \(Y\) là tích các số ghi trên hai viên bi.
c) Đại lượng \(Z\) bằng 1 nếu hai viên bi cùng màu, bằng 0 nếu hai viên bi khác màu.
Phương pháp giải:
Sử dụng khái niệm: Biến ngẫu nhiên rời rạc là một đại lượng nhận một số hữu hạn các giá trị bằng số, các giá trị này là ngẫu nhiên và không thể dự đoán trước được.
Lời giải chi tiết:
Đại lượng \(X\) có thể nhận các giá trị từ 2 đến 12.
Đại lượng \(Y\) có thể nhận các giá trị 2, 3, 4, ..., 9, 10, 12, 14, 15, 16, 18, 20, 21, 24, 25, 28, 30, 35.
Đại lượng \(Z\) có thể nhận các giá trị 0 và 1.
Vậy \(X,Y,Z\) đều là các biến ngẫu nhiên rời rạc.
Trả lời câu hỏi Luyện tập 2 trang 55 Chuyên đề học tập Toán 12 Chân trời sáng tạo
Một hộp chứa 10 tấm thẻ giống nhau, trong đó có 1 thẻ là thẻ may mắn. Bạn Khuê rút ngẫu nhiên từng thẻ trong hộp cho đến khi lấy được thẻ may mắn. Gọi \(X\) là số thẻ bạn Khuê đã rút cho đến khi lấy được thẻ may mắn. Hỏi \(X\) có phải là biến ngẫu nhiên rời rạc không nếu thẻ đã rút ra không được cho lại vào hộp?
Phương pháp giải:
Sử dụng khái niệm: Biến ngẫu nhiên rời rạc là một đại lượng nhận một số hữu hạn các giá trị bằng số, các giá trị này là ngẫu nhiên và không thể dự đoán trước được.
Lời giải chi tiết:
Do thẻ đã rút không được cho lại vào hộp nên \(X\) nhận giá trị từ 1 đến 10.
Vậy \(X\) là biến ngẫu nhiên rời rạc.
Mục 1 của Chuyên đề học tập Toán 12 - Chân trời sáng tạo thường tập trung vào một chủ đề quan trọng trong chương trình, ví dụ như đạo hàm, tích phân, hoặc các bài toán về hình học không gian. Việc nắm vững kiến thức nền tảng và phương pháp giải quyết các bài toán trong mục này là rất quan trọng để đạt kết quả tốt trong các kỳ thi sắp tới.
Các bài tập trang 54 và 55 thường bao gồm các dạng bài tập khác nhau, từ các bài tập áp dụng công thức trực tiếp đến các bài tập đòi hỏi tư duy phân tích và tổng hợp cao. Để giải quyết hiệu quả các bài tập này, các em cần:
Đề bài: (Giả định một bài tập cụ thể từ trang 54) Tính đạo hàm của hàm số f(x) = x2 + 2x - 1.
Lời giải:
Áp dụng quy tắc đạo hàm của tổng và đạo hàm của hàm số lũy thừa, ta có:
f'(x) = d/dx (x2) + d/dx (2x) - d/dx (1)
f'(x) = 2x + 2 - 0
f'(x) = 2x + 2
Trong mục 1, các em có thể gặp các dạng bài tập sau:
Để đạt hiệu quả cao trong quá trình giải bài tập, các em cần lưu ý những điều sau:
Ngoài sách giáo khoa, các em có thể tham khảo thêm các tài liệu sau để học tập và ôn luyện:
Việc giải bài tập mục 1 trang 54, 55 Chuyên đề học tập Toán 12 - Chân trời sáng tạo đòi hỏi sự nắm vững kiến thức nền tảng, khả năng phân tích đề bài, và kỹ năng giải quyết vấn đề. Hy vọng rằng với những hướng dẫn và ví dụ minh họa trên, các em sẽ tự tin hơn trong quá trình học tập và đạt kết quả tốt nhất.