Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 12 Chân trời sáng tạo tại giaitoan.edu.vn. Chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho tất cả các bài tập trong sách giáo khoa và chuyên đề học tập.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong các kỳ thi.
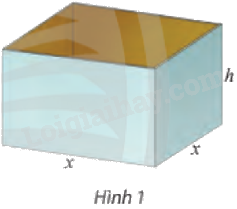
Người ta muốn sản xuất những chiếc thùng có dạng hình hộp chữ nhật không nắp, có đáy là hình vuông và thể tích chứa là (500d{m^3}) (Hình 1). Biết rằng chiều cao của thùng trong khoảng từ (3dm) đến (10dm). a) Nếu gọi độ dài cạnh đáy của thùng là (xleft( {dm} right)), chiều cao của thùng là (hleft( {dm} right)) thì tổng diện tích các mặt của thùng, kí hiệu (S), có thể được biểu thị bằng biểu thức nào? b) Có thể biểu thị tổng diện tích (S) theo (x) không? Biến (x) nhận giá t
Trả lời câu hỏi Thực hành 2 trang 18 Chuyên đề học tập Toán 12 Chân trời sáng tạo
Mặt cắt ngang của một máng dẫn nước là một hình thang cân có độ dài đáy bé bằng độ dài cạnh bên và bằng \(a\left( {cm} \right)\) không đổi (Hình 5). Gọi \(\alpha \) là một góc của hình thang cân tạo bởi đáy bé và cạnh bên \(\left( {\frac{\pi }{2} \le \alpha < \pi } \right)\). Tìm \(\alpha \) để diện tích mặt cắt ngang của máng lớn nhất.
Phương pháp giải:
• Biểu thị diện tích mặt cắt ngang của máng thông qua các đại lượng đã biết và ẩn.
• Cách tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một khoảng hay nửa khoảng bằng đạo hàm:
‒ Lập bảng biến thiên của hàm số trên tập hợp đó.
‒ Căn cứ vào bảng biến thiên, kết luận giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của hàm số.
Lời giải chi tiết:
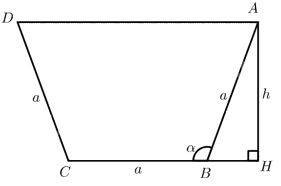
Dựng \(AH \bot BC\). Khi đó \(AH = h\) là chiều cao của mặt cắt ngang.
Ta có:
\(\begin{array}{l}\widehat {ABH} = \pi - \alpha \Rightarrow h = AB.\sin \widehat {ABH} = a\sin \left( {\pi - \alpha } \right) = a\sin \alpha \\BH = AB.\cos \widehat {ABH} = a\cos \left( {\pi - \alpha } \right) = - a\cos \alpha \\A{\rm{D}} = BC + 2BH = a - 2a\cos \alpha \end{array}\)
Diện tích của mặt cắt ngang là:
\(S = \frac{1}{2}\left( {A{\rm{D}} + BC} \right).AH = \frac{1}{2}\left( {a + a - 2{\rm{a}}\cos \alpha } \right).a\sin \alpha = {a^2}\left( {1 - \cos \alpha } \right)\sin \alpha = {a^2}\left( {\sin \alpha - \frac{1}{2}\sin 2\alpha } \right)\).
Xét hàm số \(f\left( \alpha \right) = \sin \alpha - \frac{1}{2}\sin 2\alpha \) trên \(\left[ {\frac{\pi }{2};\pi } \right)\).
Ta có: \(f'\left( \alpha \right) = \cos \alpha - \cos 2\alpha \)
\(\begin{array}{l}f'\left( \alpha \right) = 0 \Leftrightarrow \cos \alpha - \cos 2\alpha = 0 \Leftrightarrow \cos 2\alpha = \cos \alpha \\ \Leftrightarrow \left[ \begin{array}{l}2\alpha = \alpha + k2\pi \\2\alpha = - \alpha + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\alpha = k2\pi \\3\alpha = k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\alpha = k2\pi \\\alpha = k\frac{{2\pi }}{3}\end{array} \right. \Leftrightarrow \alpha = k\frac{{2\pi }}{3}\left( {k \in \mathbb{Z}} \right)\end{array}\)
Do \(\alpha \in \left[ {\frac{\pi }{2};\pi } \right)\) nên \(\alpha = \frac{{2\pi }}{3}\).
Bảng biến thiên của hàm số trên nửa khoảng \(\left[ {\frac{\pi }{2};\pi } \right)\):
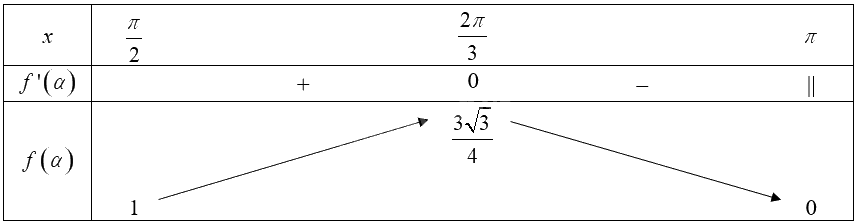
Từ bảng biến thiên, ta thấy \(\mathop {\max }\limits_{\left[ {\frac{\pi }{2};\pi } \right)} f\left( \alpha \right) = f\left( {\frac{{2\pi }}{3}} \right) = \frac{{3\sqrt 3 }}{4}\).
Vậy diện tích mặt cắt ngang của máng dẫn nước có giá trị lớn nhất bằng \({a^2}.\frac{{3\sqrt 3 }}{4} = \frac{{3{a^2}\sqrt 3 }}{4}\) khi \(\alpha = \frac{{2\pi }}{3}\).
Trả lời câu hỏi Thực hành 1 trang 17 Chuyên đề học tập Toán 12 Chân trời sáng tạo
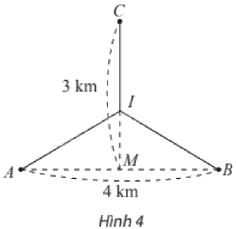
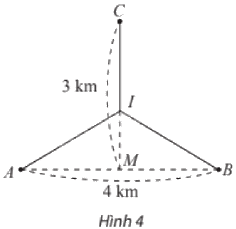
Hai nhà máy được đặt tại các vị trí \(A\) và \(B\) cách nhau 4 km. Nhà máy xử lí nước thải được đặt ở vị trí \(C\) trên đường trung trực của đoạn thẳng \(AB\), cách trung điểm \(M\) của đoạn thẳng \(AB\) một khoảng là 3 km. Người ta muốn làm đường ống dẫn nước thái từ hai nhà máy \(A,B\) đến nhà máy xử lí nước thải \(C\) gồm các đoạn thẳng \(AI,BI\) và \(IC\), với \(I\) là vị trí nằm giữa \(M\) và \(C\) (Hình 4). Cần chọn vị trí điểm \(I\) như thế nào để tổng độ dài đường ống nhỏ nhất? Tìm giá trị nhỏ nhất đó.
Phương pháp giải:
• Đặt \(IM = x\), biểu thị \(IA + IB + IC\) thông qua các đại lượng đã biết và ẩn.
• Cách tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số \(f\left( x \right)\) trên đoạn \(\left[ {a;b} \right]\):
Bước 1. Tìm các điểm \({x_1},{x_2},...,{x_n}\) thuộc khoảng \(\left( {a;b} \right)\) mà tại đó \(f'\left( x \right)\) bằng 0 hoặc không tồn tại.
Bước 2. Tính \(f\left( a \right);f\left( {{x_1}} \right);f\left( {{x_2}} \right);...;f\left( {{x_n}} \right);f\left( b \right)\).
Bước 3. Gọi \(M\) là số lớn nhất và \(m\) là số nhỏ nhất trong các giá trị tìm được ở Bước 2. Khi đó: \(M = \mathop {\max }\limits_{\left[ {a;b} \right]} f\left( x \right),m = \mathop {\min }\limits_{\left[ {a;b} \right]} f\left( x \right)\).
Lời giải chi tiết:
Đặt \(IM = x\left( {km} \right)\left( {0 \le x \le 3} \right)\).
Ta có: \(IA = IB = \sqrt {I{M^2} + M{A^2}} = \sqrt {{x^2} + 4} ;IC = MC - IM = 3 - x\)
Tổng độ dài đường ống là: \(IA + IB + IC = 2\sqrt {{x^2} + 4} + 3 - x\).
Xét hàm số \(f\left( x \right) = 2\sqrt {{x^2} + 4} + 3 - x\) trên đoạn \(\left[ {0;3} \right]\).
Ta có: \(f'\left( x \right) = 2.\frac{{{{\left( {{x^2} + 4} \right)}^\prime }}}{{2\sqrt {{x^2} + 4} }} - 1 = 2.\frac{{2{\rm{x}}}}{{2\sqrt {{x^2} + 4} }} - 1 = \frac{{2{\rm{x}}}}{{\sqrt {{x^2} + 4} }} - 1\)
\(f'\left( x \right) = 0 \Leftrightarrow \frac{{2{\rm{x}}}}{{\sqrt {{x^2} + 4} }} = 1 \Leftrightarrow 2{\rm{x}} = \sqrt {{x^2} + 4} \Leftrightarrow 4{{\rm{x}}^2} = {x^2} + 4 \Leftrightarrow {x^2} = \frac{4}{3} \Leftrightarrow x = \frac{2}{{\sqrt 3 }}\) hoặc \(x = - \frac{2}{{\sqrt 3 }}\) (loại).
\(f\left( 0 \right) = 7;f\left( {\frac{2}{{\sqrt 3 }}} \right) = 3 + 2\sqrt 3 ;f\left( 3 \right) = 2\sqrt {13} \).
Vậy \(\mathop {\min }\limits_{\left[ {0;3} \right]} f\left( x \right) = f\left( {\frac{2}{{\sqrt 3 }}} \right) = 3 + 2\sqrt 3 \).
Vậy \(IM = \frac{2}{{\sqrt 3 }} \approx 1,155\left( {km} \right)\) thì tổng độ dài đường ống nhỏ nhất bằng \(3 + 2\sqrt 3 \approx 6,464\left( {km} \right)\).
Trả lời câu hỏi Hoạt động 1 trang 15 Chuyên đề học tập Toán 12 Chân trời sáng tạo
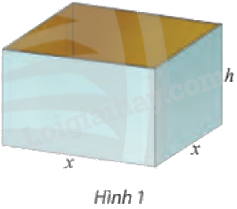
Người ta muốn sản xuất những chiếc thùng có dạng hình hộp chữ nhật không nắp, có đáy là hình vuông và thể tích chứa là \(500d{m^3}\) (Hình 1). Biết rằng chiều cao của thùng trong khoảng từ \(3dm\) đến \(10dm\).a) Nếu gọi độ dài cạnh đáy của thùng là \(x\left( {dm} \right)\), chiều cao của thùng là \(h\left( {dm} \right)\) thì tổng diện tích các mặt của thùng, kí hiệu \(S\), có thể được biểu thị bằng biểu thức nào?b) Có thể biểu thị tổng diện tích \(S\) theo \(x\) không? Biến \(x\) nhận giá trị trong miền nào? c) Với giá trị nào của \(x\) thì \(S\) có giá trị nhỏ nhất?
Phương pháp giải:
• Biểu thị \(S\) thông qua các đại lượng đã biết và ẩn.
• Cách tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một khoảng hay nửa khoảng bằng đạo hàm:
‒ Lập bảng biến thiên của hàm số trên tập hợp đó.
‒ Căn cứ vào bảng biến thiên, kết luận giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của hàm số.
Lời giải chi tiết:
a) Gọi độ dài cạnh đáy của thùng là \(x\left( {dm} \right)\), chiều cao của thùng là \(h\left( {dm} \right)\).
Diện tích xung quang của thùng là: \(4{\rm{x}}{\rm{.h}}\left( {d{m^2}} \right)\).
Diện tích đáy của thùng là: \({x^2}\left( {d{m^2}} \right)\).
Tổng diện tích các mặt của thùng là: \(S = {x^2} + 4{\rm{x}}h\left( {d{m^2}} \right)\) với \(x > 0,3 \le h \le 10\).
b) Từ giả thiết \(V = {x^2}h \Leftrightarrow 500 = {x^2}h \Leftrightarrow h = \frac{{500}}{{{x^2}}}\).
Khi đó \(S = {x^2} + 4\,.\,\frac{{500}}{{{x^2}}}x = {x^2} + \frac{{2000}}{x}\left( {x > 0} \right)\).
c) Ta có: \(S' = 2{\rm{x}} - \frac{{2000}}{{{x^2}}}\)
\(S' = 0 \Leftrightarrow x = 10\).
Bảng biến thiên của hàm số trên khoảng \(\left( {0; + \infty } \right)\):

Từ bảng biến thiên, ta thấy \(\mathop {\min }\limits_{\left( {0; + \infty } \right)} S = f\left( {10} \right) = 300\). Khi đó \(h = \frac{{500}}{{{{10}^2}}} = 5\left( {dm} \right)\) thoả mãn điều kiện \(3 \le h \le 10\).
Vậy với \(x = 10\left( {dm} \right)\) thì \(S\) có giá trị nhỏ nhất.
Trả lời câu hỏi Hoạt động 1 trang 15 Chuyên đề học tập Toán 12 Chân trời sáng tạo
Người ta muốn sản xuất những chiếc thùng có dạng hình hộp chữ nhật không nắp, có đáy là hình vuông và thể tích chứa là \(500d{m^3}\) (Hình 1). Biết rằng chiều cao của thùng trong khoảng từ \(3dm\) đến \(10dm\).a) Nếu gọi độ dài cạnh đáy của thùng là \(x\left( {dm} \right)\), chiều cao của thùng là \(h\left( {dm} \right)\) thì tổng diện tích các mặt của thùng, kí hiệu \(S\), có thể được biểu thị bằng biểu thức nào?b) Có thể biểu thị tổng diện tích \(S\) theo \(x\) không? Biến \(x\) nhận giá trị trong miền nào? c) Với giá trị nào của \(x\) thì \(S\) có giá trị nhỏ nhất?
Phương pháp giải:
• Biểu thị \(S\) thông qua các đại lượng đã biết và ẩn.
• Cách tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một khoảng hay nửa khoảng bằng đạo hàm:
‒ Lập bảng biến thiên của hàm số trên tập hợp đó.
‒ Căn cứ vào bảng biến thiên, kết luận giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của hàm số.
Lời giải chi tiết:
a) Gọi độ dài cạnh đáy của thùng là \(x\left( {dm} \right)\), chiều cao của thùng là \(h\left( {dm} \right)\).
Diện tích xung quang của thùng là: \(4{\rm{x}}{\rm{.h}}\left( {d{m^2}} \right)\).
Diện tích đáy của thùng là: \({x^2}\left( {d{m^2}} \right)\).
Tổng diện tích các mặt của thùng là: \(S = {x^2} + 4{\rm{x}}h\left( {d{m^2}} \right)\) với \(x > 0,3 \le h \le 10\).
b) Từ giả thiết \(V = {x^2}h \Leftrightarrow 500 = {x^2}h \Leftrightarrow h = \frac{{500}}{{{x^2}}}\).
Khi đó \(S = {x^2} + 4\,.\,\frac{{500}}{{{x^2}}}x = {x^2} + \frac{{2000}}{x}\left( {x > 0} \right)\).
c) Ta có: \(S' = 2{\rm{x}} - \frac{{2000}}{{{x^2}}}\)
\(S' = 0 \Leftrightarrow x = 10\).
Bảng biến thiên của hàm số trên khoảng \(\left( {0; + \infty } \right)\):

Từ bảng biến thiên, ta thấy \(\mathop {\min }\limits_{\left( {0; + \infty } \right)} S = f\left( {10} \right) = 300\). Khi đó \(h = \frac{{500}}{{{{10}^2}}} = 5\left( {dm} \right)\) thoả mãn điều kiện \(3 \le h \le 10\).
Vậy với \(x = 10\left( {dm} \right)\) thì \(S\) có giá trị nhỏ nhất.
Trả lời câu hỏi Thực hành 1 trang 17 Chuyên đề học tập Toán 12 Chân trời sáng tạo
Hai nhà máy được đặt tại các vị trí \(A\) và \(B\) cách nhau 4 km. Nhà máy xử lí nước thải được đặt ở vị trí \(C\) trên đường trung trực của đoạn thẳng \(AB\), cách trung điểm \(M\) của đoạn thẳng \(AB\) một khoảng là 3 km. Người ta muốn làm đường ống dẫn nước thái từ hai nhà máy \(A,B\) đến nhà máy xử lí nước thải \(C\) gồm các đoạn thẳng \(AI,BI\) và \(IC\), với \(I\) là vị trí nằm giữa \(M\) và \(C\) (Hình 4). Cần chọn vị trí điểm \(I\) như thế nào để tổng độ dài đường ống nhỏ nhất? Tìm giá trị nhỏ nhất đó.
Phương pháp giải:
• Đặt \(IM = x\), biểu thị \(IA + IB + IC\) thông qua các đại lượng đã biết và ẩn.
• Cách tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số \(f\left( x \right)\) trên đoạn \(\left[ {a;b} \right]\):
Bước 1. Tìm các điểm \({x_1},{x_2},...,{x_n}\) thuộc khoảng \(\left( {a;b} \right)\) mà tại đó \(f'\left( x \right)\) bằng 0 hoặc không tồn tại.
Bước 2. Tính \(f\left( a \right);f\left( {{x_1}} \right);f\left( {{x_2}} \right);...;f\left( {{x_n}} \right);f\left( b \right)\).
Bước 3. Gọi \(M\) là số lớn nhất và \(m\) là số nhỏ nhất trong các giá trị tìm được ở Bước 2. Khi đó: \(M = \mathop {\max }\limits_{\left[ {a;b} \right]} f\left( x \right),m = \mathop {\min }\limits_{\left[ {a;b} \right]} f\left( x \right)\).
Lời giải chi tiết:
Đặt \(IM = x\left( {km} \right)\left( {0 \le x \le 3} \right)\).
Ta có: \(IA = IB = \sqrt {I{M^2} + M{A^2}} = \sqrt {{x^2} + 4} ;IC = MC - IM = 3 - x\)
Tổng độ dài đường ống là: \(IA + IB + IC = 2\sqrt {{x^2} + 4} + 3 - x\).
Xét hàm số \(f\left( x \right) = 2\sqrt {{x^2} + 4} + 3 - x\) trên đoạn \(\left[ {0;3} \right]\).
Ta có: \(f'\left( x \right) = 2.\frac{{{{\left( {{x^2} + 4} \right)}^\prime }}}{{2\sqrt {{x^2} + 4} }} - 1 = 2.\frac{{2{\rm{x}}}}{{2\sqrt {{x^2} + 4} }} - 1 = \frac{{2{\rm{x}}}}{{\sqrt {{x^2} + 4} }} - 1\)
\(f'\left( x \right) = 0 \Leftrightarrow \frac{{2{\rm{x}}}}{{\sqrt {{x^2} + 4} }} = 1 \Leftrightarrow 2{\rm{x}} = \sqrt {{x^2} + 4} \Leftrightarrow 4{{\rm{x}}^2} = {x^2} + 4 \Leftrightarrow {x^2} = \frac{4}{3} \Leftrightarrow x = \frac{2}{{\sqrt 3 }}\) hoặc \(x = - \frac{2}{{\sqrt 3 }}\) (loại).
\(f\left( 0 \right) = 7;f\left( {\frac{2}{{\sqrt 3 }}} \right) = 3 + 2\sqrt 3 ;f\left( 3 \right) = 2\sqrt {13} \).
Vậy \(\mathop {\min }\limits_{\left[ {0;3} \right]} f\left( x \right) = f\left( {\frac{2}{{\sqrt 3 }}} \right) = 3 + 2\sqrt 3 \).
Vậy \(IM = \frac{2}{{\sqrt 3 }} \approx 1,155\left( {km} \right)\) thì tổng độ dài đường ống nhỏ nhất bằng \(3 + 2\sqrt 3 \approx 6,464\left( {km} \right)\).
Trả lời câu hỏi Thực hành 2 trang 18 Chuyên đề học tập Toán 12 Chân trời sáng tạo
Mặt cắt ngang của một máng dẫn nước là một hình thang cân có độ dài đáy bé bằng độ dài cạnh bên và bằng \(a\left( {cm} \right)\) không đổi (Hình 5). Gọi \(\alpha \) là một góc của hình thang cân tạo bởi đáy bé và cạnh bên \(\left( {\frac{\pi }{2} \le \alpha < \pi } \right)\). Tìm \(\alpha \) để diện tích mặt cắt ngang của máng lớn nhất.
Phương pháp giải:
• Biểu thị diện tích mặt cắt ngang của máng thông qua các đại lượng đã biết và ẩn.
• Cách tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một khoảng hay nửa khoảng bằng đạo hàm:
‒ Lập bảng biến thiên của hàm số trên tập hợp đó.
‒ Căn cứ vào bảng biến thiên, kết luận giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của hàm số.
Lời giải chi tiết:
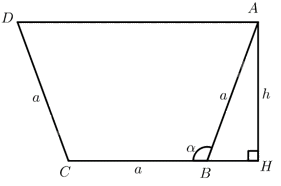
Dựng \(AH \bot BC\). Khi đó \(AH = h\) là chiều cao của mặt cắt ngang.
Ta có:
\(\begin{array}{l}\widehat {ABH} = \pi - \alpha \Rightarrow h = AB.\sin \widehat {ABH} = a\sin \left( {\pi - \alpha } \right) = a\sin \alpha \\BH = AB.\cos \widehat {ABH} = a\cos \left( {\pi - \alpha } \right) = - a\cos \alpha \\A{\rm{D}} = BC + 2BH = a - 2a\cos \alpha \end{array}\)
Diện tích của mặt cắt ngang là:
\(S = \frac{1}{2}\left( {A{\rm{D}} + BC} \right).AH = \frac{1}{2}\left( {a + a - 2{\rm{a}}\cos \alpha } \right).a\sin \alpha = {a^2}\left( {1 - \cos \alpha } \right)\sin \alpha = {a^2}\left( {\sin \alpha - \frac{1}{2}\sin 2\alpha } \right)\).
Xét hàm số \(f\left( \alpha \right) = \sin \alpha - \frac{1}{2}\sin 2\alpha \) trên \(\left[ {\frac{\pi }{2};\pi } \right)\).
Ta có: \(f'\left( \alpha \right) = \cos \alpha - \cos 2\alpha \)
\(\begin{array}{l}f'\left( \alpha \right) = 0 \Leftrightarrow \cos \alpha - \cos 2\alpha = 0 \Leftrightarrow \cos 2\alpha = \cos \alpha \\ \Leftrightarrow \left[ \begin{array}{l}2\alpha = \alpha + k2\pi \\2\alpha = - \alpha + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\alpha = k2\pi \\3\alpha = k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\alpha = k2\pi \\\alpha = k\frac{{2\pi }}{3}\end{array} \right. \Leftrightarrow \alpha = k\frac{{2\pi }}{3}\left( {k \in \mathbb{Z}} \right)\end{array}\)
Do \(\alpha \in \left[ {\frac{\pi }{2};\pi } \right)\) nên \(\alpha = \frac{{2\pi }}{3}\).
Bảng biến thiên của hàm số trên nửa khoảng \(\left[ {\frac{\pi }{2};\pi } \right)\):
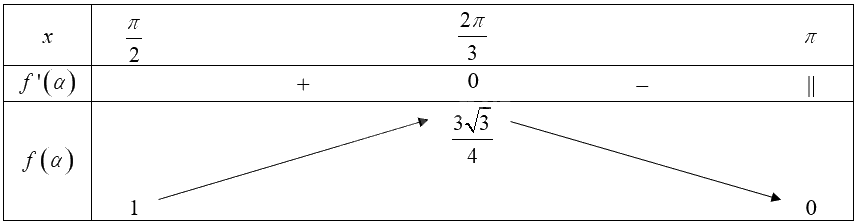
Từ bảng biến thiên, ta thấy \(\mathop {\max }\limits_{\left[ {\frac{\pi }{2};\pi } \right)} f\left( \alpha \right) = f\left( {\frac{{2\pi }}{3}} \right) = \frac{{3\sqrt 3 }}{4}\).
Vậy diện tích mặt cắt ngang của máng dẫn nước có giá trị lớn nhất bằng \({a^2}.\frac{{3\sqrt 3 }}{4} = \frac{{3{a^2}\sqrt 3 }}{4}\) khi \(\alpha = \frac{{2\pi }}{3}\).
Chuyên đề học tập Toán 12 - Chân trời sáng tạo là một tài liệu bổ trợ quan trọng giúp học sinh củng cố kiến thức và rèn luyện kỹ năng giải các bài toán nâng cao. Mục 1 của chuyên đề này thường tập trung vào một chủ đề cụ thể, đòi hỏi học sinh phải nắm vững lý thuyết và áp dụng linh hoạt các công thức, định lý đã học. Việc giải các bài tập trang 15, 16, 17, 18 là bước quan trọng để kiểm tra và đánh giá mức độ hiểu bài của học sinh.
Ở trang 15, các bài tập thường xoay quanh việc xác định các yếu tố của hàm số bậc hai (hệ số a, b, c), tìm đỉnh của parabol, vẽ đồ thị hàm số và xét tính đơn điệu, cực trị. Để giải các bài tập này, học sinh cần nắm vững các công thức liên quan đến hàm số bậc hai và biết cách áp dụng chúng một cách chính xác.
Trang 16 tập trung vào việc giải các bất phương trình bậc hai, xét dấu của tam thức bậc hai và ứng dụng vào các bài toán thực tế. Học sinh cần nắm vững các phương pháp giải bất phương trình bậc hai và biết cách xác định khoảng nghiệm của bất phương trình.
Trang 17 và 18 thường chứa các bài tập tổng hợp, kết hợp nhiều kiến thức và kỹ năng đã học. Các bài tập này có độ khó cao hơn, đòi hỏi học sinh phải có khả năng phân tích, tổng hợp và vận dụng linh hoạt các kiến thức đã học. Ngoài ra, các bài tập này cũng có thể liên quan đến các chủ đề khác trong chương trình Toán 12.
Để giải các bài tập Toán 12 Chân trời sáng tạo một cách hiệu quả, học sinh cần:
Giaitoan.edu.vn là một website học toán online uy tín, cung cấp:
Việc giải bài tập mục 1 trang 15, 16, 17, 18 Chuyên đề học tập Toán 12 - Chân trời sáng tạo là một bước quan trọng trong quá trình học tập Toán 12. Hy vọng rằng với những lời giải chi tiết và phương pháp giải bài tập hiệu quả mà giaitoan.edu.vn cung cấp, các em học sinh sẽ đạt được kết quả tốt nhất trong môn Toán.