Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 12 Chân trời sáng tạo. Bài viết này sẽ hướng dẫn bạn giải bài 11 trang 51 một cách đầy đủ và chính xác.
Chúng tôi luôn cố gắng mang đến những phương pháp giải toán hiệu quả, giúp bạn nắm vững kiến thức và tự tin hơn trong các kỳ thi.
Tỉ lệ phần trăm giá cả trung bình của hàng hoá và dịch vụ của Việt Nam năm sau so với năm trước được cho trong bảng sau: Hãy tính tỉ lệ lạm phát của Việt Nam trong các năm từ 2017 đến 2021.
Đề bài
Tỉ lệ phần trăm giá cả trung bình của hàng hoá và dịch vụ của Việt Nam năm sau so với năm trước được cho trong bảng sau:
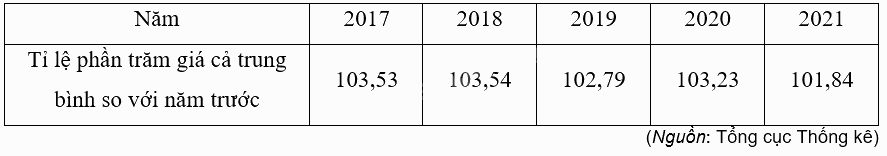
Hãy tính tỉ lệ lạm phát của Việt Nam trong các năm từ 2017 đến 2021.
Phương pháp giải - Xem chi tiết
Tỉ lệ lạm phát của năm sau so với năm trước là: \(i = \frac{A}{P} - 1\).
Lời giải chi tiết
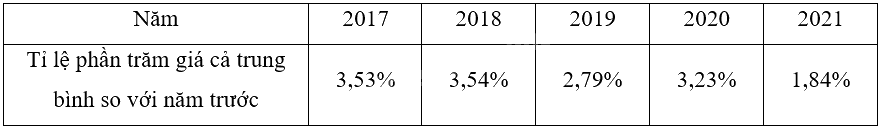
Bài 11 trang 51 Chuyên đề học tập Toán 12 - Chân trời sáng tạo thuộc chương trình học Toán 12, tập trung vào việc vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế. Bài tập này thường yêu cầu học sinh phân tích hàm số, tìm cực trị, và khảo sát sự biến thiên của hàm số. Việc nắm vững các khái niệm và kỹ năng liên quan đến đạo hàm là vô cùng quan trọng để giải quyết bài toán này một cách hiệu quả.
Trước khi bắt đầu giải bài tập, chúng ta cần đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Trong bài 11 trang 51, yêu cầu thường là tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một khoảng cho trước, hoặc tìm điều kiện để hàm số có cực trị. Việc xác định đúng yêu cầu sẽ giúp chúng ta lựa chọn phương pháp giải phù hợp.
Để giải bài tập về đạo hàm, chúng ta có thể áp dụng các phương pháp sau:
(Phần này sẽ chứa lời giải chi tiết cho bài 11 trang 51, bao gồm các bước tính toán, giải thích rõ ràng và kết luận.)
Để giúp bạn hiểu rõ hơn về phương pháp giải bài tập về đạo hàm, chúng ta sẽ xem xét một số ví dụ minh họa và bài tập tương tự:
Khi giải bài tập về đạo hàm, bạn cần lưu ý những điều sau:
Đạo hàm có rất nhiều ứng dụng trong thực tế, chẳng hạn như:
Bài 11 trang 51 Chuyên đề học tập Toán 12 - Chân trời sáng tạo là một bài tập quan trọng giúp bạn rèn luyện kỹ năng giải bài tập về đạo hàm. Hy vọng rằng, với những hướng dẫn chi tiết và ví dụ minh họa trong bài viết này, bạn sẽ tự tin hơn trong việc giải quyết các bài toán tương tự.