Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài 12 trang 23 Chuyên đề học tập Toán 12 - Chân trời sáng tạo. Bài viết này cung cấp phương pháp giải bài tập, đáp án chính xác và giải thích rõ ràng từng bước để giúp học sinh hiểu sâu kiến thức.
Chúng tôi luôn cập nhật nhanh chóng và chính xác các lời giải bài tập Toán 12, đáp ứng nhu cầu học tập của học sinh trên toàn quốc.
Theo kết quả thăm dò trước một buổi biểu diễn văn nghệ ngoài trời, nếu giá bán mỗi vé là (p) nghìn đồng thì sẽ có ({rm{x}}) người mua vé xem biểu diễn, giữa (p) và ({rm{x}}) có mối liên hệ: (p = 500.{e^{ - 0,0005x}}). Đơn vị tổ chức nên bán vé với giá bao nhiêu thì đạt được doanh thu (tổng số tiền bán vé) cao nhất?
Đề bài
Theo kết quả thăm dò trước một buổi biểu diễn văn nghệ ngoài trời, nếu giá bán mỗi vé là \(p\) nghìn đồng thì sẽ có \({\rm{x}}\) người mua vé xem biểu diễn, giữa \(p\) và \({\rm{x}}\) có mối liên hệ: \(p = 500.{e^{ - 0,0005x}}\). Đơn vị tổ chức nên bán vé với giá bao nhiêu thì đạt được doanh thu (tổng số tiền bán vé) cao nhất?
Phương pháp giải - Xem chi tiết
• Biểu thị doanh thu thông qua \(p\) và \({\rm{x}}\).
• Cách tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một khoảng hay nửa khoảng bằng đạo hàm:
‒ Lập bảng biến thiên của hàm số trên tập hợp đó.
‒ Căn cứ vào bảng biến thiên, kết luận giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của hàm số.
Lời giải chi tiết
Doanh thu khi công ty bán được \(x\) vé với mỗi vé là \(p\) nghìn đồng là:
\(R\left( x \right) = p.x = 500.{e^{ - 0,0005x}}.x\) (triệu đồng)
Xét hàm số \(R\left( x \right) = 500.{e^{ - 0,0005x}}.x\) trên khoảng \(\left( {0; + \infty } \right)\).
Ta có:
\(\begin{array}{l}R'\left( x \right) = {\left( {500.{e^{ - 0,0005x}}} \right)^\prime }.x + 500.{e^{ - 0,0005x}}.{\left( x \right)^\prime } = 500.\left( { - 0,0005} \right).{e^{ - 0,0005x}}.x + 500.{e^{ - 0,0005x}}\\ = 500.{e^{ - 0,0005x}}\left( {1 - 0,0005x} \right)\end{array}\)
\(R'\left( x \right) = 0 \Leftrightarrow 500.{e^{ - 0,0005x}}\left( {1 - 0,0005x} \right) = 0 \Leftrightarrow x = 2000\).
Bảng biến thiên của hàm số trên khoảng \(\left( {0; + \infty } \right)\):
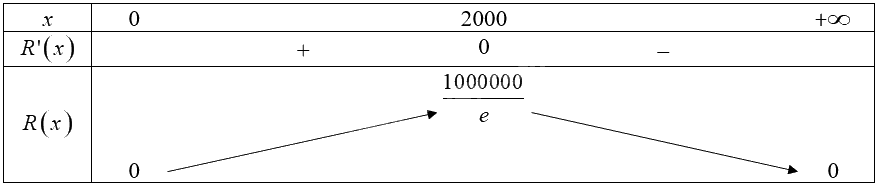
Từ bảng biến thiên, ta thấy \(\mathop {\max }\limits_{\left( {0; + \infty } \right)} R\left( x \right) = R\left( {2000} \right) = \frac{{1000000}}{e}\).
Vậy đơn vị tổ chức nên bán vé với giá \(p = 500.{e^{ - 0,0005.2000}} = \frac{{500}}{e} \approx 184\) nghìn đồng thì đạt được doanh thu (tổng số tiền bán vé) cao nhất.
Bài 12 trang 23 Chuyên đề học tập Toán 12 - Chân trời sáng tạo thuộc chương trình học Toán 12, tập trung vào việc vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế. Bài tập này yêu cầu học sinh nắm vững các khái niệm về đạo hàm, quy tắc tính đạo hàm và ứng dụng của đạo hàm trong việc tìm cực trị, khoảng đơn điệu của hàm số.
Bài 12 thường xoay quanh các dạng bài sau:
Để giải quyết bài 12 trang 23 Chuyên đề học tập Toán 12 - Chân trời sáng tạo một cách hiệu quả, học sinh cần thực hiện các bước sau:
Bài tập: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số f(x) = x3 - 3x2 + 2 trên đoạn [-1; 3].
Giải:
Khi giải bài tập về đạo hàm, học sinh cần lưu ý một số điểm sau:
Để học tập và ôn luyện kiến thức về đạo hàm, học sinh có thể tham khảo các tài liệu sau:
Bài 12 trang 23 Chuyên đề học tập Toán 12 - Chân trời sáng tạo là một bài tập quan trọng giúp học sinh củng cố kiến thức về đạo hàm và ứng dụng của đạo hàm. Hy vọng với lời giải chi tiết và phương pháp giải bài tập được trình bày trong bài viết này, học sinh sẽ tự tin hơn khi giải quyết các bài toán tương tự.