Chào mừng các em học sinh đến với lời giải chi tiết bài 3 trang 22 Chuyên đề học tập Toán 12 - Chân trời sáng tạo. Bài viết này sẽ cung cấp cho các em phương pháp giải bài tập hiệu quả, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán.
Một nhà phân phối có thể thuê tối đa 3 chiếc xe tải loại A và 8 chiếc xe tải loại B để vận chuyển 100 chiếc máy giặt từ nhà máy sản xuất đến nơi tiêu thụ. Mỗi xe loại A chở được tối đa 20 máy giặt với giá cước 3 triệu đồng mỗi chuyến, mỗi xe loại B chở được tối đa 10 máy giặt với giá cước 2 triệu đồng mỗi chuyến. Nếu mỗi xe chỉ chở nhiều nhất một chuyến, số tiền cước tối thiểu (triệu đồng) mà nhà phân phối phải trả là A. 19. B. 17. C. 15. D. 25.
Đề bài
Một nhà phân phối có thể thuê tối đa 3 chiếc xe tải loại A và 8 chiếc xe tải loại B để vận chuyển 100 chiếc máy giặt từ nhà máy sản xuất đến nơi tiêu thụ. Mỗi xe loại A chở được tối đa 20 máy giặt với giá cước 3 triệu đồng mỗi chuyến, mỗi xe loại B chở được tối đa 10 máy giặt với giá cước 2 triệu đồng mỗi chuyến. Nếu mỗi xe chỉ chở nhiều nhất một chuyến, số tiền cước tối thiểu (triệu đồng) mà nhà phân phối phải trả là
A. 19.
B. 17.
C. 15.
D. 25.
Phương pháp giải - Xem chi tiết
Bước 1: Đặt hai ẩn biểu thị hai đại lượng chưa biết (cần tìm). Viết điều kiện có nghĩa cho các ẩn đó.
Bước 2: Từ dữ kiện của bài toán, viết biểu thức biểu thị đại lượng cần tìm giá trị tối ưu và các bất phương trình bậc nhất đối với hai ẩn trên. Từ đó phát biểu bài toán quy hoạch tuyến tính nhận được.
Bước 3: Giải bài toán quy hoạch tuyến tính và trả lời.
Lời giải chi tiết
Gọi \(x,y\) \(\left( {x \ge 0,y \ge 0} \right)\) lần lượt là số xe tải loại A và loại B.
Một nhà phân phối có thể thuê tối đa 3 chiếc xe tải loại A và 8 chiếc xe tải loại B nên ta có \(0 \le x \le 3\) và \(0 \le y \le 8\).
Số máy giặt hai loại xe chở được là: \(20{\rm{x}} + 10y\).
Cần vận chuyển 100 máy giặt nên ta có \(20{\rm{x}} + 10y \ge 100\) hay \(2{\rm{x}} + y \ge 10\).
Số tiền cước mà nhà phân phối phải trả là \(F = 3x + 2y\) (triệu đồng).
Từ đó, ta cần giải bài toán quy hoạch tuyến tính: \(F = 3x + 2y \to \min \) với ràng buộc \(\left\{ \begin{array}{l}2{\rm{x}} + y \ge 10\\0 \le x \le 3\\0 \le y \le 8\end{array} \right.\)
Tập phương án \({\Omega }\) là miền tam giác \(ABC\).
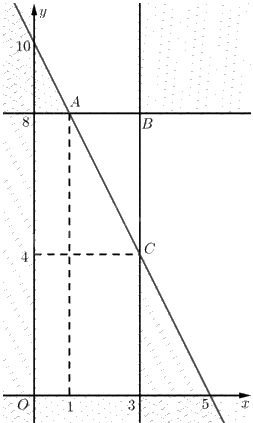
Ta có \(A\left( {1;8} \right),B\left( {3;8} \right),C\left( {3;4} \right)\).
Giá trị của biểu thức \(F\) tại các đỉnh của \({\Omega }\):
\(F\left( {1;8} \right) = 19,F\left( {3;8} \right) = 25,F\left( {3;4} \right) = 17\)
Do đó: \(\mathop {\min }\limits_{\Omega } F = F\left( {3;4} \right) = 17\).
Vậy số tiền cước tối thiểu (triệu đồng) mà nhà phân phối phải trả là 17 triệu đồng.
Chọn B
Bài 3 trang 22 Chuyên đề học tập Toán 12 - Chân trời sáng tạo thuộc chương trình học Toán 12, tập trung vào việc vận dụng các kiến thức về đạo hàm để giải quyết các bài toán thực tế. Bài tập này thường yêu cầu học sinh phải hiểu rõ các khái niệm về đạo hàm, quy tắc tính đạo hàm và ứng dụng của đạo hàm trong việc tìm cực trị, khoảng đơn điệu của hàm số.
Bài 3 thường bao gồm các dạng bài tập sau:
Để giúp các em hiểu rõ hơn về cách giải bài 3 trang 22, chúng ta sẽ đi vào phân tích từng dạng bài tập cụ thể.
Để tính đạo hàm của hàm số, các em cần nắm vững các quy tắc tính đạo hàm cơ bản, bao gồm:
Ví dụ: Cho hàm số y = x2 + 2x + 1. Tính đạo hàm của hàm số.
Lời giải: y' = 2x + 2
Để tìm cực trị của hàm số, các em cần thực hiện các bước sau:
Ví dụ: Tìm cực trị của hàm số y = x3 - 3x + 2.
Lời giải:
Để khảo sát sự biến thiên của hàm số, các em cần thực hiện các bước sau:
Các bài toán tối ưu thường yêu cầu tìm giá trị lớn nhất hoặc nhỏ nhất của một hàm số trên một khoảng xác định. Để giải các bài toán này, các em cần thực hiện các bước sau:
Khi giải bài 3 trang 22, các em cần lưu ý những điều sau:
Bài 3 trang 22 Chuyên đề học tập Toán 12 - Chân trời sáng tạo là một bài tập quan trọng giúp các em củng cố kiến thức về đạo hàm và ứng dụng của đạo hàm. Hy vọng với lời giải chi tiết và những lưu ý trên, các em sẽ tự tin hơn trong quá trình học tập và giải bài tập.