Giải bài 2 trang 21 Chuyên đề học tập Toán 12 - Chân trời sáng tạo

Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài 2 trang 21 Chuyên đề học tập Toán 12 - Chân trời sáng tạo. Bài viết này cung cấp đáp án chính xác, phương pháp giải rõ ràng, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.

Chúng tôi luôn cập nhật nhanh chóng và chính xác các lời giải bài tập Toán 12, đáp ứng nhu cầu học tập của học sinh trên toàn quốc.

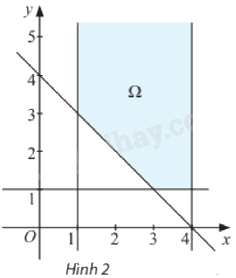
Giá trị nhỏ nhất của biểu thức (Fleft( {x;y} right) = 5x + 2y) trên miền ({Omega }) ở Hình 2 là A. 11. B. 17. C. 7. D. 20.

Đề bài

Giá trị nhỏ nhất của biểu thức \(F\left( {x;y} \right) = 5x + 2y\) trên miền \({\Omega }\) ở Hình 2 là

A. 11.

B. 17.

C. 7.

D. 20.

Phương pháp giải - Xem chi tiết Giải bài 2 trang 21 Chuyên đề học tập Toán 12 - Chân trời sáng tạo 2

Trong trường hợp tập phương án không là miền đa giác nằm trong góc phần tư thứ nhất và các hệ số \(a\) và \(b\) không âm thì giá trị nhỏ nhất trong các giá trị này là giá trị nhỏ nhất của \(F\) trên \({\Omega }\).

Lời giải chi tiết

Do \({\Omega }\) nằm trong góc phần tư thứ nhất và các hệ số của biểu thức \(F\left( {x;y} \right) = 5x + 2y\) đều dương nên \(F\) đạt giá trị nhỏ nhất tại một đỉnh của \({\Omega }\).

Ta có \(F\left( {1;3} \right) = 11;F\left( {3;1} \right) = 17;F\left( {4;1} \right) = 22\).

Do đó \(\mathop {\min }\limits_{\Omega } F = F\left( {1;3} \right) = 11\).

Chọn A

Tự tin bứt phá Kỳ thi THPT Quốc gia môn Toán! Đừng bỏ lỡ Giải bài 2 trang 21 Chuyên đề học tập Toán 12 - Chân trời sáng tạo đặc sắc thuộc chuyên mục sgk toán 12 trên nền tảng toán. Với bộ bài tập toán trung học phổ thông được biên soạn chuyên sâu, bám sát cấu trúc đề thi và chương trình Toán 12, đây chính là "chiến lược vàng" giúp các em tối ưu hóa ôn luyện. Học sinh sẽ không chỉ làm chủ mọi dạng bài thi mà còn nắm vững chiến thuật làm bài hiệu quả, sẵn sàng tự tin chinh phục điểm cao, vững bước vào đại học mơ ước nhờ phương pháp học trực quan, khoa học và hiệu quả học tập vượt trội!

Giải bài 2 trang 21 Chuyên đề học tập Toán 12 - Chân trời sáng tạo: Tổng quan

Bài 2 trang 21 Chuyên đề học tập Toán 12 - Chân trời sáng tạo thuộc chương trình học Toán 12, tập trung vào việc vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế. Bài tập này yêu cầu học sinh hiểu rõ các khái niệm về đạo hàm, quy tắc tính đạo hàm và ứng dụng của đạo hàm trong việc tìm cực trị, khoảng đơn điệu của hàm số.

Nội dung bài tập

Bài 2 thường xoay quanh việc xét tính đơn điệu của hàm số. Cụ thể, học sinh cần:

Tính đạo hàm của hàm số.
Xác định các điểm mà đạo hàm bằng 0 hoặc không xác định.
Lập bảng biến thiên để xác định khoảng đồng biến, nghịch biến của hàm số.
Kết luận về tính đơn điệu của hàm số.

Phương pháp giải chi tiết

Để giải bài 2 trang 21 Chuyên đề học tập Toán 12 - Chân trời sáng tạo một cách hiệu quả, học sinh cần nắm vững các bước sau:

Bước 1: Xác định tập xác định của hàm số. Điều này giúp đảm bảo rằng các phép toán đạo hàm được thực hiện trên tập xác định của hàm số.
Bước 2: Tính đạo hàm của hàm số. Sử dụng các quy tắc tính đạo hàm đã học để tìm đạo hàm f'(x) của hàm số f(x).
Bước 3: Tìm các điểm tới hạn. Giải phương trình f'(x) = 0 để tìm các điểm mà đạo hàm bằng 0. Ngoài ra, cần xác định các điểm mà đạo hàm không xác định.
Bước 4: Lập bảng biến thiên. Sử dụng các điểm tới hạn để chia tập xác định của hàm số thành các khoảng. Xét dấu của đạo hàm trên mỗi khoảng để xác định khoảng đồng biến, nghịch biến của hàm số.
Bước 5: Kết luận về tính đơn điệu của hàm số. Dựa vào bảng biến thiên, kết luận về khoảng đồng biến, nghịch biến của hàm số.

Ví dụ minh họa

Giả sử hàm số f(x) = x³ - 3x² + 2. Ta sẽ giải bài 2 trang 21 Chuyên đề học tập Toán 12 - Chân trời sáng tạo cho hàm số này:

Bước 1: Tập xác định: R
Bước 2: Đạo hàm: f'(x) = 3x² - 6x
Bước 3: Điểm tới hạn: 3x² - 6x = 0 => x = 0 hoặc x = 2
Bước 4: Bảng biến thiên:
x -∞ 0 2 +∞
f'(x) + - +
f(x) Đồng biến Nghịch biến Đồng biến
Bước 5: Kết luận: Hàm số đồng biến trên các khoảng (-∞; 0) và (2; +∞), nghịch biến trên khoảng (0; 2).

x	-∞	0	2	+∞
f'(x)	+	-	+
f(x)	Đồng biến	Nghịch biến	Đồng biến

Lưu ý quan trọng

Khi giải bài 2 trang 21 Chuyên đề học tập Toán 12 - Chân trời sáng tạo, học sinh cần chú ý:

Kiểm tra kỹ tập xác định của hàm số.
Tính đạo hàm chính xác.
Lập bảng biến thiên cẩn thận.
Kết luận về tính đơn điệu của hàm số một cách chính xác.

Ứng dụng của việc giải bài tập

Việc giải bài 2 trang 21 Chuyên đề học tập Toán 12 - Chân trời sáng tạo không chỉ giúp học sinh nắm vững kiến thức về đạo hàm và tính đơn điệu của hàm số mà còn có ứng dụng thực tế trong nhiều lĩnh vực khác nhau, như kinh tế, kỹ thuật, vật lý,...

Giaitoan.edu.vn: Hỗ trợ học tập Toán 12

Giaitoan.edu.vn là địa chỉ tin cậy dành cho học sinh, sinh viên và những người yêu thích môn Toán. Chúng tôi cung cấp đầy đủ các lời giải bài tập Toán 12, đáp án trắc nghiệm, kiến thức lý thuyết và các bài giảng online chất lượng cao. Hãy truy cập giaitoan.edu.vn để học Toán 12 hiệu quả hơn!