Giải bài 2 trang 63 Chuyên đề học tập Toán 12 - Chân trời sáng tạo

Chào mừng các em học sinh đến với lời giải chi tiết bài 2 trang 63 Chuyên đề học tập Toán 12 - Chân trời sáng tạo. Bài viết này sẽ cung cấp cho các em phương pháp giải bài tập hiệu quả, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.

Giaitoan.edu.vn là địa chỉ tin cậy dành cho các em học sinh muốn tìm kiếm lời giải bài tập Toán nhanh chóng và chính xác.

Sau khi khảo sát hiệu quả sử dụng của các cột sạc ô tô điện ở một khu vực, người ta thu được bảng phân bố xác suất của số lượng xe, kí hiệu là X, sạc điện ở mỗi cột sạc trong một ngày như sau: a) Tìm (p). b) Hỏi trung bình một ngày có bao nhiêu xe được sạc điện ở một cột sạc? c) Tính độ lệch chuẩn của (X).

Đề bài

Sau khi khảo sát hiệu quả sử dụng của các cột sạc ô tô điện ở một khu vực, người ta thu được bảng phân bố xác suất của số lượng xe, kí hiệu là X, sạc điện ở mỗi cột sạc trong một ngày như sau:

Giải bài 2 trang 63 Chuyên đề học tập Toán 12 - Chân trời sáng tạo 1 a) Tìm \(p\). b) Hỏi trung bình một ngày có bao nhiêu xe được sạc điện ở một cột sạc? c) Tính độ lệch chuẩn của \(X\).

Phương pháp giải - Xem chi tiết Giải bài 2 trang 63 Chuyên đề học tập Toán 12 - Chân trời sáng tạo 2

Giả sử biến ngẫu nhiên rời rạc \(X\) có bảng phân bố xác suất như sau:

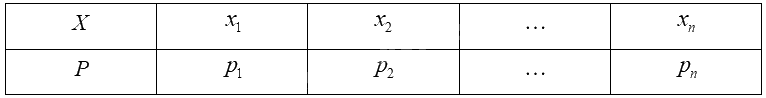
Giải bài 2 trang 63 Chuyên đề học tập Toán 12 - Chân trời sáng tạo 3

Kì vọng của \(X\) được tính bởi công thức: \(E\left( X \right) = {x_1}{p_1} + {x_2}{p_2} + ... + {x_n}{p_n}\).

Phương sai của \(X\) được tính bởi công thức: \(V\left( X \right) = x_1^2{p_1} + x_2^2{p_2} + ... + x_n^2{p_n} - {\left[ {E\left( X \right)} \right]^2}\).

Độ lệch chuẩn của \(X\) được tính bởi công thức: \(\sigma \left( X \right) = \sqrt {V\left( X \right)} \).

Lời giải chi tiết

a) Ta có: \(0,1 + p + 4p + 3p + p = 1 \Leftrightarrow 0,1 + 9p = 1 \Leftrightarrow p = 0,1\).

b) Bảng phân bố xác suất của \(X\):

Giải bài 2 trang 63 Chuyên đề học tập Toán 12 - Chân trời sáng tạo 4

Kì vọng của \(X\) là: \(E\left( X \right) = 0.0,1 + 1.0,1 + 2.0,4 + 3.0,3 + 4.0,1 = 2,2\).

Trung bình một ngày có 2,2 xe được sạc điện ở một cột sạc.

c) Phương sai của \(X\) là: \(V\left( X \right) = {0^2}.0,1 + {1^2}.0,1 + {2^2}.0,4 + {3^2}.0,3 + {4^2}.0,1 - {2,2^2} = 1,16\).

Phương sai của \(X\) là: \(\sigma \left( X \right) = \sqrt {1,16} \approx 1,08\).

Tự tin bứt phá Kỳ thi THPT Quốc gia môn Toán! Đừng bỏ lỡ Giải bài 2 trang 63 Chuyên đề học tập Toán 12 - Chân trời sáng tạo đặc sắc thuộc chuyên mục sgk toán 12 trên nền tảng tài liệu toán. Với bộ bài tập toán trung học phổ thông được biên soạn chuyên sâu, bám sát cấu trúc đề thi và chương trình Toán 12, đây chính là "chiến lược vàng" giúp các em tối ưu hóa ôn luyện. Học sinh sẽ không chỉ làm chủ mọi dạng bài thi mà còn nắm vững chiến thuật làm bài hiệu quả, sẵn sàng tự tin chinh phục điểm cao, vững bước vào đại học mơ ước nhờ phương pháp học trực quan, khoa học và hiệu quả học tập vượt trội!

Giải bài 2 trang 63 Chuyên đề học tập Toán 12 - Chân trời sáng tạo: Tổng quan

Bài 2 trang 63 Chuyên đề học tập Toán 12 - Chân trời sáng tạo thuộc chương trình học Toán 12, tập trung vào việc vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế. Bài tập này yêu cầu học sinh phải hiểu rõ các khái niệm về đạo hàm, quy tắc tính đạo hàm và ứng dụng của đạo hàm trong việc tìm cực trị, khoảng đơn điệu của hàm số.

Nội dung bài tập

Bài 2 thường xoay quanh các dạng bài sau:

Tìm đạo hàm của hàm số: Yêu cầu tính đạo hàm của các hàm số phức tạp, bao gồm hàm số đa thức, hàm số lượng giác, hàm số mũ, hàm số logarit và hàm số hợp.
Giải phương trình đạo hàm: Yêu cầu giải các phương trình đạo hàm để tìm các điểm cực trị, điểm uốn của hàm số.
Khảo sát hàm số: Yêu cầu khảo sát sự biến thiên của hàm số, xác định khoảng đồng biến, nghịch biến, cực đại, cực tiểu và điểm uốn.
Ứng dụng đạo hàm vào các bài toán thực tế: Yêu cầu giải các bài toán tối ưu hóa, bài toán liên quan đến vận tốc, gia tốc, hoặc các bài toán kinh tế.

Phương pháp giải bài tập

Để giải bài 2 trang 63 Chuyên đề học tập Toán 12 - Chân trời sáng tạo một cách hiệu quả, các em cần nắm vững các bước sau:

Xác định đúng công thức đạo hàm: Lựa chọn công thức đạo hàm phù hợp với từng loại hàm số.
Tính đạo hàm một cách chính xác: Thực hiện các phép tính đạo hàm cẩn thận, tránh sai sót.
Giải phương trình đạo hàm: Sử dụng các phương pháp giải phương trình đã học để tìm ra nghiệm.
Phân tích kết quả: Đánh giá các nghiệm tìm được, xác định các điểm cực trị, điểm uốn và khoảng đơn điệu của hàm số.
Kiểm tra lại kết quả: So sánh kết quả với các điều kiện của bài toán để đảm bảo tính chính xác.

Ví dụ minh họa

Bài toán: Cho hàm số y = x³ - 3x² + 2. Tìm các điểm cực trị của hàm số.

Lời giải:

Tính đạo hàm: y' = 3x² - 6x
Giải phương trình y' = 0: 3x² - 6x = 0 => x = 0 hoặc x = 2
Xác định các điểm cực trị:
- Tại x = 0, y'' = 6x - 6 = -6 < 0 => Hàm số đạt cực đại tại x = 0, y = 2
- Tại x = 2, y'' = 6x - 6 = 6 > 0 => Hàm số đạt cực tiểu tại x = 2, y = -2
Kết luận: Hàm số đạt cực đại tại điểm (0, 2) và cực tiểu tại điểm (2, -2).

Lưu ý khi giải bài tập

Trong quá trình giải bài tập, các em cần lưu ý những điều sau:

Nắm vững các định nghĩa và tính chất của đạo hàm.
Thực hành tính đạo hàm thường xuyên để nâng cao kỹ năng.
Sử dụng máy tính bỏ túi để kiểm tra kết quả.
Tham khảo các tài liệu tham khảo và bài giảng trên mạng.
Hỏi thầy cô giáo hoặc bạn bè khi gặp khó khăn.

Tài liệu tham khảo

Các em có thể tham khảo thêm các tài liệu sau để học tập và ôn luyện:

Sách giáo khoa Toán 12 - Chân trời sáng tạo
Sách bài tập Toán 12 - Chân trời sáng tạo
Các trang web học Toán online uy tín như giaitoan.edu.vn
Các video bài giảng trên YouTube

Kết luận

Hy vọng với những hướng dẫn chi tiết và ví dụ minh họa trên, các em sẽ tự tin hơn trong việc giải bài 2 trang 63 Chuyên đề học tập Toán 12 - Chân trời sáng tạo. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!