Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong Chuyên đề học tập Toán 12 - Chân trời sáng tạo. Chúng tôi hiểu rằng việc giải các bài tập Toán đôi khi có thể gặp khó khăn, đặc biệt là với những chuyên đề phức tạp.
Với mục tiêu hỗ trợ học sinh học tập hiệu quả, chúng tôi đã biên soạn và kiểm tra kỹ lưỡng lời giải cho từng bài tập trong mục 4, trang 60, 61, 62, 63.
Cho hai biến ngẫu nhiên rời rạc (X) và (Y) có bảng phân bố xác suất như sau: a) Hãy so sánh kì vọng của X và kì vọng của Y. b) Biến ngẫu nhiên rời rạc nào có các giá trị “phân tán” rộng hơn?
Trả lời câu hỏi Luyện tập 5 trang 61 Chuyên đề học tập Toán 12 Chân trời sáng tạo
Hãy tính \(V\left( Y \right)\) ở Ví dụ 8 bằng công thức (1).
Phương pháp giải:
Giả sử biến ngẫu nhiên rời rạc \(X\) có bảng phân bố xác suất như sau:
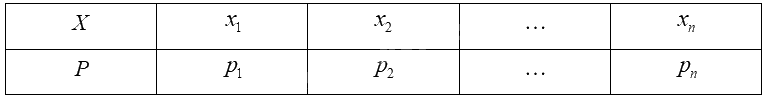
Phương sai của \(X\) được tính bởi công thức: \(V\left( X \right) = x_1^2{p_1} + x_2^2{p_2} + ... + x_n^2{p_n} - {\left[ {E\left( X \right)} \right]^2}\).
Lời giải chi tiết:
Kì vọng của \(Y\) là: \(E\left( Y \right) = - 200.0,25 + 2.0,5 + 200.0,25 = 1\).
Phương sai của \(X\) là: \(V\left( X \right) = {\left( { - 200} \right)^2}.0,25 + {2^2}.0,5 + {200^2}.0,25 - {1^2} = 20001\).
Trả lời câu hỏi Luyện tập 6 trang 63 Chuyên đề học tập Toán 12 Chân trời sáng tạo
Mỗi ngày trong tuần, bác Linh sẽ chọn một trong ba phương tiện là xe đạp, xe máy hoặc xe buýt để đi đến cơ quan. Thời gian đi từ nhà đến cơ quan khi đi bằng xe đạp, xe máy hoặc xe buýt lần lượt là 20 phút, 10 phút và 12 phút. Biết rằng xác suất bác Linh chọn xe đạp, xe máy và xe buýt lần lượt là 0,3; 0,5 và 0,2. Chọn ngẫu nhiên một ngày trong tuần và gọi \(X\) là thời gian bác Linh đi từ nhà đến cơ quan ngày hôm đó. Tính kì vọng và phương sai của \(X\).
Phương pháp giải:
Giả sử biến ngẫu nhiên rời rạc \(X\) có bảng phân bố xác suất như sau:
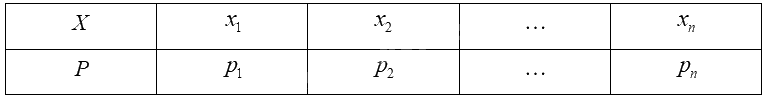
Kì vọng của \(X\) được tính bởi công thức: \(E\left( X \right) = {x_1}{p_1} + {x_2}{p_2} + ... + {x_n}{p_n}\).
Phương sai của \(X\) được tính bởi công thức: \(V\left( X \right) = x_1^2{p_1} + x_2^2{p_2} + ... + x_n^2{p_n} - {\left[ {E\left( X \right)} \right]^2}\).
Lời giải chi tiết:
Bảng phân bố xác suất của \(X\):

Kì vọng của \(X\) là: \(E\left( X \right) = 10.0,5 + 12.0,2 + 20.0,3 = 13,4\).
Phương sai của \(X\) là: \(V\left( X \right) = {10^2}.0,5 + {12^2}.0,2 + {20^2}.0,3 - {13,4^2} = 19,24\).
Trả lời câu hỏi Hoạt động 4 trang 60 Chuyên đề học tập Toán 12 Chân trời sáng tạo
Cho hai biến ngẫu nhiên rời rạc \(X\) và \(Y\) có bảng phân bố xác suất như sau:
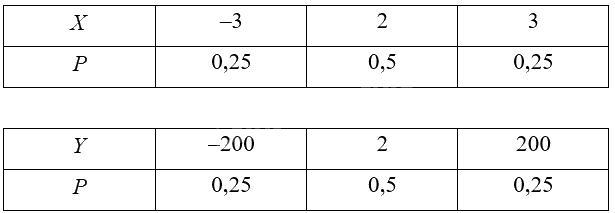
a) Hãy so sánh kì vọng của X và kì vọng của Y.
b) Biến ngẫu nhiên rời rạc nào có các giá trị “phân tán” rộng hơn?
Phương pháp giải:
Giả sử biến ngẫu nhiên rời rạc \(X\) có bảng phân bố xác suất như sau:
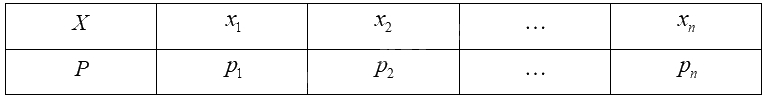
Kì vọng của \(X\) được tính bởi công thức: \(E\left( X \right) = {x_1}{p_1} + {x_2}{p_2} + ... + {x_n}{p_n}\).
Lời giải chi tiết:
a) Kì vọng của \(X\) là: \(E\left( X \right) = - 3.0,25 + 2.0,5 + 3.0,25 = 1\).
Kì vọng của \(Y\) là: \(E\left( Y \right) = - 200.0,25 + 2.0,5 + 200.0,25 = 1\).
b) Y có độ phân tán rộng hơn.
Trả lời câu hỏi Vận dụng 2 trang 63 Chuyên đề học tập Toán 12 Chân trời sáng tạo
Hai xạ thủ Vinh và Huy cùng tập bắn vào một bia. Xác suất bắn trúng vòng 9 và 10 của xạ thủ Vinh lần lượt là 0,4 và 0,3. Xác suất bắn trúng vòng 9 và 10 của xạ thủ Huy lần lượt là 0,6 và 0,2. Điểm số xạ thủ đạt được khi bắn trúng vòng 10 và 9 lần lượt là 2 và 1. Nếu xạ thủ không bắn trúng hai vòng trên thì được 0 điểm.
a) Nếu so sánh theo kì vọng thì xạ thủ nào có kết quả bắn tốt hơn?
b) Nếu so sánh theo phương sai thì xạ thủ nào có kết quả bắn ổn định hơn?
Phương pháp giải:
Giả sử biến ngẫu nhiên rời rạc \(X\) có bảng phân bố xác suất như sau:
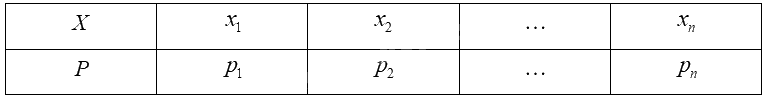
Kì vọng của \(X\) được tính bởi công thức: \(E\left( X \right) = {x_1}{p_1} + {x_2}{p_2} + ... + {x_n}{p_n}\).
Phương sai của \(X\) được tính bởi công thức: \(V\left( X \right) = x_1^2{p_1} + x_2^2{p_2} + ... + x_n^2{p_n} - {\left[ {E\left( X \right)} \right]^2}\).
Lời giải chi tiết:
Gọi \(X\) và \(Y\) lần lượt là điểm của xạ thủ Vinh và xạ thủ Huy.
Xác suất để xạ thủ Vinh được 0 điểm là: \(1 - 0,4 - 0,3 = 0,3\).
Xác suất để xạ thủ Huy được 0 điểm là: \(1 - 0,6 - 0,2 = 0,2\).
Bảng phân bố xác suất của \(X\):

Bảng phân bố xác suất của \(Y\):

a) Kì vọng của \(X\) là: \(E\left( X \right) = 0.0,3 + 1.0,4 + 2.0,3 = 1\).
Kì vọng của \(Y\) là: \(E\left( Y \right) = 0.0,2 + 1.0,6 + 2.0,2 = 1\).
Vậy nếu so sánh theo kì vọng thì hai xạ thủ có kết quả bắn tốt như nhau.
b) Phương sai của \(X\) là: \(V\left( X \right) = {0^2}.0,3 + {1^2}.0,4 + {2^2}.0,3 - {1^2} = 0,6\).
Phương sai của \(Y\) là: \(V\left( Y \right) = {0^2}.0,2 + {1^2}.0,6 + {2^2}.0,2 - {1^2} = 0,4\).
Vậy nếu so sánh theo phương sai thì xạ thủ Huy có kết quả bắn ổn định hơn.
Trả lời câu hỏi Hoạt động 4 trang 60 Chuyên đề học tập Toán 12 Chân trời sáng tạo
Cho hai biến ngẫu nhiên rời rạc \(X\) và \(Y\) có bảng phân bố xác suất như sau:
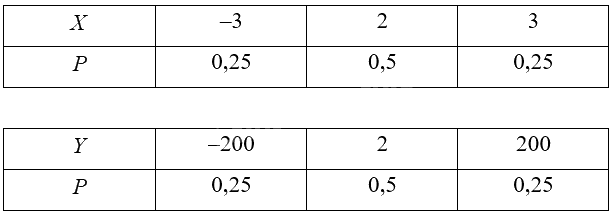
a) Hãy so sánh kì vọng của X và kì vọng của Y.
b) Biến ngẫu nhiên rời rạc nào có các giá trị “phân tán” rộng hơn?
Phương pháp giải:
Giả sử biến ngẫu nhiên rời rạc \(X\) có bảng phân bố xác suất như sau:
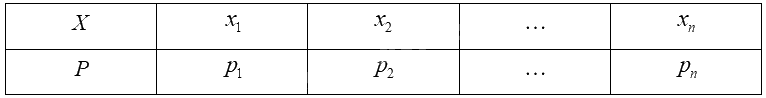
Kì vọng của \(X\) được tính bởi công thức: \(E\left( X \right) = {x_1}{p_1} + {x_2}{p_2} + ... + {x_n}{p_n}\).
Lời giải chi tiết:
a) Kì vọng của \(X\) là: \(E\left( X \right) = - 3.0,25 + 2.0,5 + 3.0,25 = 1\).
Kì vọng của \(Y\) là: \(E\left( Y \right) = - 200.0,25 + 2.0,5 + 200.0,25 = 1\).
b) Y có độ phân tán rộng hơn.
Trả lời câu hỏi Luyện tập 5 trang 61 Chuyên đề học tập Toán 12 Chân trời sáng tạo
Hãy tính \(V\left( Y \right)\) ở Ví dụ 8 bằng công thức (1).
Phương pháp giải:
Giả sử biến ngẫu nhiên rời rạc \(X\) có bảng phân bố xác suất như sau:
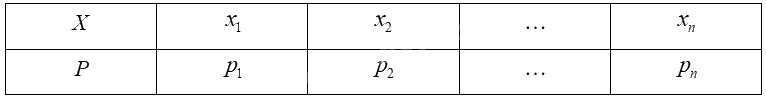
Phương sai của \(X\) được tính bởi công thức: \(V\left( X \right) = x_1^2{p_1} + x_2^2{p_2} + ... + x_n^2{p_n} - {\left[ {E\left( X \right)} \right]^2}\).
Lời giải chi tiết:
Kì vọng của \(Y\) là: \(E\left( Y \right) = - 200.0,25 + 2.0,5 + 200.0,25 = 1\).
Phương sai của \(X\) là: \(V\left( X \right) = {\left( { - 200} \right)^2}.0,25 + {2^2}.0,5 + {200^2}.0,25 - {1^2} = 20001\).
Trả lời câu hỏi Luyện tập 6 trang 63 Chuyên đề học tập Toán 12 Chân trời sáng tạo
Mỗi ngày trong tuần, bác Linh sẽ chọn một trong ba phương tiện là xe đạp, xe máy hoặc xe buýt để đi đến cơ quan. Thời gian đi từ nhà đến cơ quan khi đi bằng xe đạp, xe máy hoặc xe buýt lần lượt là 20 phút, 10 phút và 12 phút. Biết rằng xác suất bác Linh chọn xe đạp, xe máy và xe buýt lần lượt là 0,3; 0,5 và 0,2. Chọn ngẫu nhiên một ngày trong tuần và gọi \(X\) là thời gian bác Linh đi từ nhà đến cơ quan ngày hôm đó. Tính kì vọng và phương sai của \(X\).
Phương pháp giải:
Giả sử biến ngẫu nhiên rời rạc \(X\) có bảng phân bố xác suất như sau:
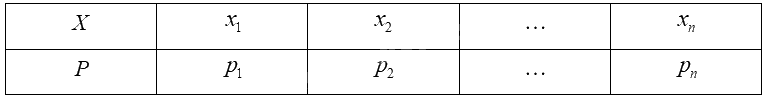
Kì vọng của \(X\) được tính bởi công thức: \(E\left( X \right) = {x_1}{p_1} + {x_2}{p_2} + ... + {x_n}{p_n}\).
Phương sai của \(X\) được tính bởi công thức: \(V\left( X \right) = x_1^2{p_1} + x_2^2{p_2} + ... + x_n^2{p_n} - {\left[ {E\left( X \right)} \right]^2}\).
Lời giải chi tiết:
Bảng phân bố xác suất của \(X\):

Kì vọng của \(X\) là: \(E\left( X \right) = 10.0,5 + 12.0,2 + 20.0,3 = 13,4\).
Phương sai của \(X\) là: \(V\left( X \right) = {10^2}.0,5 + {12^2}.0,2 + {20^2}.0,3 - {13,4^2} = 19,24\).
Trả lời câu hỏi Vận dụng 2 trang 63 Chuyên đề học tập Toán 12 Chân trời sáng tạo
Hai xạ thủ Vinh và Huy cùng tập bắn vào một bia. Xác suất bắn trúng vòng 9 và 10 của xạ thủ Vinh lần lượt là 0,4 và 0,3. Xác suất bắn trúng vòng 9 và 10 của xạ thủ Huy lần lượt là 0,6 và 0,2. Điểm số xạ thủ đạt được khi bắn trúng vòng 10 và 9 lần lượt là 2 và 1. Nếu xạ thủ không bắn trúng hai vòng trên thì được 0 điểm.
a) Nếu so sánh theo kì vọng thì xạ thủ nào có kết quả bắn tốt hơn?
b) Nếu so sánh theo phương sai thì xạ thủ nào có kết quả bắn ổn định hơn?
Phương pháp giải:
Giả sử biến ngẫu nhiên rời rạc \(X\) có bảng phân bố xác suất như sau:
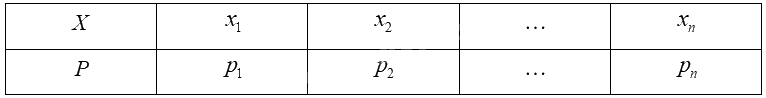
Kì vọng của \(X\) được tính bởi công thức: \(E\left( X \right) = {x_1}{p_1} + {x_2}{p_2} + ... + {x_n}{p_n}\).
Phương sai của \(X\) được tính bởi công thức: \(V\left( X \right) = x_1^2{p_1} + x_2^2{p_2} + ... + x_n^2{p_n} - {\left[ {E\left( X \right)} \right]^2}\).
Lời giải chi tiết:
Gọi \(X\) và \(Y\) lần lượt là điểm của xạ thủ Vinh và xạ thủ Huy.
Xác suất để xạ thủ Vinh được 0 điểm là: \(1 - 0,4 - 0,3 = 0,3\).
Xác suất để xạ thủ Huy được 0 điểm là: \(1 - 0,6 - 0,2 = 0,2\).
Bảng phân bố xác suất của \(X\):

Bảng phân bố xác suất của \(Y\):

a) Kì vọng của \(X\) là: \(E\left( X \right) = 0.0,3 + 1.0,4 + 2.0,3 = 1\).
Kì vọng của \(Y\) là: \(E\left( Y \right) = 0.0,2 + 1.0,6 + 2.0,2 = 1\).
Vậy nếu so sánh theo kì vọng thì hai xạ thủ có kết quả bắn tốt như nhau.
b) Phương sai của \(X\) là: \(V\left( X \right) = {0^2}.0,3 + {1^2}.0,4 + {2^2}.0,3 - {1^2} = 0,6\).
Phương sai của \(Y\) là: \(V\left( Y \right) = {0^2}.0,2 + {1^2}.0,6 + {2^2}.0,2 - {1^2} = 0,4\).
Vậy nếu so sánh theo phương sai thì xạ thủ Huy có kết quả bắn ổn định hơn.
Mục 4 của Chuyên đề học tập Toán 12 - Chân trời sáng tạo thường tập trung vào một chủ đề cụ thể trong chương trình Toán học. Để giải quyết hiệu quả các bài tập trong mục này, học sinh cần nắm vững kiến thức lý thuyết, hiểu rõ các định nghĩa, định lý và công thức liên quan. Ngoài ra, việc luyện tập thường xuyên với các bài tập khác nhau cũng rất quan trọng để củng cố kiến thức và rèn luyện kỹ năng giải toán.
Trang 60 thường chứa các bài tập áp dụng trực tiếp các kiến thức đã học trong phần lý thuyết. Các bài tập này thường có dạng bài tập cơ bản, giúp học sinh làm quen với việc sử dụng các công thức và định lý. Để giải các bài tập này, học sinh cần xác định đúng các yếu tố đầu vào, áp dụng công thức phù hợp và thực hiện các phép tính chính xác.
Trang 61 thường chứa các bài tập có tính chất mở rộng và nâng cao hơn so với trang 60. Các bài tập này đòi hỏi học sinh phải có khả năng tư duy logic, phân tích và tổng hợp thông tin. Để giải các bài tập này, học sinh cần hiểu sâu sắc các khái niệm và định lý, đồng thời có khả năng vận dụng linh hoạt các kiến thức đã học vào các tình huống khác nhau.
Trang 62 thường chứa các bài tập kết hợp nhiều kiến thức khác nhau. Các bài tập này đòi hỏi học sinh phải có khả năng liên kết các kiến thức lại với nhau để giải quyết vấn đề. Để giải các bài tập này, học sinh cần xác định rõ các kiến thức liên quan, phân tích mối quan hệ giữa chúng và áp dụng các phương pháp giải phù hợp.
Trang 63 thường chứa các bài tập ứng dụng thực tế. Các bài tập này giúp học sinh hiểu rõ hơn về tầm quan trọng của Toán học trong cuộc sống. Để giải các bài tập này, học sinh cần hiểu rõ các tình huống thực tế, xác định các yếu tố toán học liên quan và áp dụng các kiến thức đã học để giải quyết vấn đề.
| Công thức | Mô tả |
|---|---|
| Công thức A | Giải thích công thức A |
| Công thức B | Giải thích công thức B |
Hy vọng rằng với những hướng dẫn chi tiết và các mẹo giải toán hiệu quả trên đây, các bạn học sinh sẽ tự tin hơn khi giải các bài tập trong mục 4 trang 60, 61, 62, 63 Chuyên đề học tập Toán 12 - Chân trời sáng tạo. Chúc các bạn học tập tốt và đạt kết quả cao!