Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 12 Chân trời sáng tạo tại giaitoan.edu.vn. Chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho từng bài tập trong mục 2 của chuyên đề, giúp các em nắm vững kiến thức và tự tin làm bài.
Với đội ngũ giáo viên giàu kinh nghiệm, chúng tôi cam kết mang đến cho các em những giải pháp học tập hiệu quả nhất. Hãy cùng giaitoan.edu.vn khám phá và chinh phục những thử thách trong môn Toán nhé!
Ông An đầu tư 1 tỉ đồng vào chứng chỉ quỹ tín dụng Q với lãi suất 10%/năm theo phương thức tính lãi kép trong thời gian 2 năm. Tính số tiền ông An nhận được sau 2 năm nếu kì trả lãi là 6 tháng, 3 tháng.
Trả lời câu hỏi Luyện tập 1 trang 44 Chuyên đề học tập Toán 12 Chân trời sáng tạo
Ông An đầu tư 1 tỉ đồng vào chứng chỉ quỹ tín dụng Q với lãi suất 10%/năm theo phương thức tính lãi kép trong thời gian 2 năm. Tính số tiền ông An nhận được sau 2 năm nếu kì trả lãi là 6 tháng, 3 tháng.
Phương pháp giải:
Giá trị cả vốn lẫn lãi sau \(n\) chu kì lãi kép: \({F_n} = P{\left( {1 + r} \right)^n}\) (với \(P\): vốn gốc, \(r\): lãi suất trên một kì hạn, \(n\): số kì hạn).
Lời giải chi tiết:
Với kì trả lãi 6 tháng, ta có: \(P = 1;r = \frac{6}{{12}}.10\% = 5\% ;n = 4\).
Số tiền ông An nhận được sau 2 năm là:
\(F = P{\left( {1 + r} \right)^4} = 1.{\left( {1 + 5\% } \right)^4} \approx 1,216\) (tỉ đồng).
Với kì trả lãi 3 tháng, ta có: \(P = 1;r = \frac{3}{{12}}.10\% = 2,5\% ;n = 8\).
Số tiền ông An nhận được sau 2 năm là:
\(F = P{\left( {1 + r} \right)^8} = 1.{\left( {1 + 2,5\% } \right)^8} \approx 1,218\) (tỉ đồng).
Trả lời câu hỏi Luyện tập 4 trang 44 Chuyên đề học tập Toán 12 Chân trời sáng tạo
Ông Sơn tạo ra một dòng tiền bằng cách cuối mỗi năm đều gửi tiết kiệm 100 triệu đồng vào ngân hàng với lãi suất 9%/năm theo phương thức tính lãi kép với kì hạn 1 năm. Hỏi sau bao lâu thì ông Sơn có đủ 2 tỉ đồng để mua một mảnh đất?
Phương pháp giải:
Sử dụng công thức: \(n = \frac{{\ln \left( {\frac{{F{\rm{r}}}}{A} + 1} \right)}}{{\ln \left( {1 + r} \right)}}\) (với \(F\): số tiền người đó thu được ở cuối dòng tiền, \(A\): số tiền gửi từng kì hạn, \(r\): lãi suất trên một kì hạn, \(n\): số kì hạn).
Lời giải chi tiết:
Ta có: \(F = 2,r = 9\% ,A = 0,1\).
\(n = \frac{{\ln \left( {\frac{{F{\rm{r}}}}{A} + 1} \right)}}{{\ln \left( {1 + r} \right)}} = \frac{{\ln \left( {\frac{{2.9\% }}{{0,1}} + 1} \right)}}{{\ln \left( {1 + 9\% } \right)}} \approx 11,95\).
Vậy sau 12 năm thì ông Sơn có đủ 2 tỉ đồng để mua một mảnh đất.
Trả lời câu hỏi Luyện tập 2 trang 44 Chuyên đề học tập Toán 12 Chân trời sáng tạo
Mỗi cổ phiếu của công ty X có giá bán 25 000 đồng và lợi nhuận trên mỗi cổ phiếu được công bố là 2 500 đồng/năm. Mỗi cổ phiếu của công ty Y có giá bán 10 000 đồng và lợi nhuận trên mỗi cổ phiếu được công bố là 500 đồng/năm.
a) Tính tỉ số phần trăm giữa giá bán và lợi nhuận trên mỗi cổ phiếu của công ty X và công ty Y (kết quả làm tròn đến hàng phần mười).
b) Nếu các nhà đầu tư có xu hướng thích mua các cổ phiếu được định giá thấp so với lợi nhuận thì cổ phiếu nào có giá trị đầu tư cao hơn?
Phương pháp giải:
Tính tỉ số phần trăm giữa giá bán và lợi nhuận.
Lời giải chi tiết:
a) Tỉ số phần trăm giữa giá bán và lợi nhuận trên mỗi cổ phiếu của công ty X là:
\(P/E = \frac{{25000}}{{2500}} = 1000\% \).
Tỉ số phần trăm giữa giá bán và lợi nhuận trên mỗi cổ phiếu của công ty Y là:
\(P/E = \frac{{10000}}{{500}} = 2000\% \).
b) Vì tỉ số phần trăm giữa giá bán và lợi nhuận trên mỗi cổ phiếu của công ty X nhỏ hơn tỉ số phần trăm giữa giá bán và lợi nhuận trên mỗi cổ phiếu của công ty Y nên cổ phiếu của công ty X có giá trị đầu tư cao hơn.
Trả lời câu hỏi Luyện tập 3 trang 44 Chuyên đề học tập Toán 12 Chân trời sáng tạo
Một công ty có ngân sách chi tiêu là \(T\) đồng, nếu giữ tiền mặt \({\rm{x}}\) đồng và đầu tư \(\left( {T - x} \right)\) đồng thì sẽ có lợi nhuận là:
\(f\left( x \right) = \frac{{a\left( {T - x} \right)}}{2} - \frac{{bT}}{x}\),
trong đó:
\(x\): số tiền mặt cần giữ, \(x \in \left( {0;T} \right]\);
\(a\): lãi suất đầu tư 28%;
\(b\): chi phí mỗi lần rút tiền mặt 20,5%.
Tìm \(x\) để \(f\left( x \right)\) đạt giá trị lớn nhất khi \(T = 12\) tỉ đồng.
Phương pháp giải:
Cách tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một khoảng hay nửa khoảng bằng đạo hàm:
‒ Lập bảng biến thiên của hàm số trên tập hợp đó.
‒ Căn cứ vào bảng biến thiên, kết luận giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của hàm số.
Lời giải chi tiết:
Xét hàm số \(f\left( x \right) = \frac{{28\% \left( {12 - x} \right)}}{2} - \frac{{12.20,5\% }}{x} = 0,14\left( {12 - x} \right) - \frac{{2,46}}{x} = 1,68 - 0,14x - \frac{{2,46}}{x}\) trên \(\left( {0;12} \right]\).
Ta có: \(f'\left( x \right) = - 0,14 + \frac{{2,46}}{{{x^2}}}\)
\(f'\left( x \right) = 0 \Leftrightarrow - 0,14 + \frac{{2,46}}{{{x^2}}} = 0 \Leftrightarrow {x^2} = \frac{{123}}{7} \Leftrightarrow x = \frac{{\sqrt {861} }}{7}\) hoặc \(x = - \frac{{\sqrt {861} }}{7}\) (loại).
Bảng biến thiên của hàm số trên nửa khoảng \(\left( {0;12} \right]\):
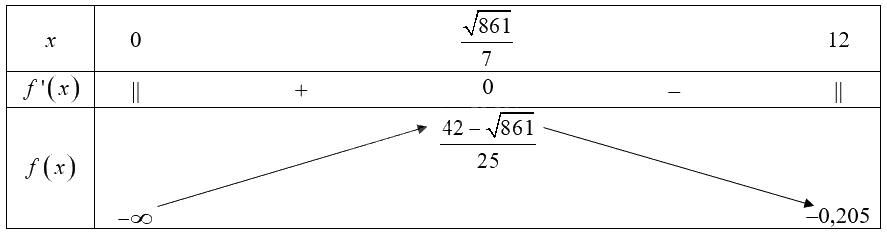
Từ bảng biến thiên, ta thấy \(\mathop {\max }\limits_{\left( {0;12} \right]} f\left( x \right) = f\left( {\frac{{\sqrt {861} }}{7}} \right) = \frac{{42 - \sqrt {861} }}{{25}}\).
Vậy \(x = \frac{{\sqrt {861} }}{7} \approx 4,2\) (tỉ đồng) để \(f\left( x \right)\) đạt giá trị lớn nhất.
Trả lời câu hỏi Hoạt động 2 trang 45 Chuyên đề học tập Toán 12 Chân trời sáng tạo
Bạn Nam là một sinh viên năm nhất thuê nhà trọ để học đại học. Dưới đây là bảng thu chi trong sổ tay của bạn Nam.
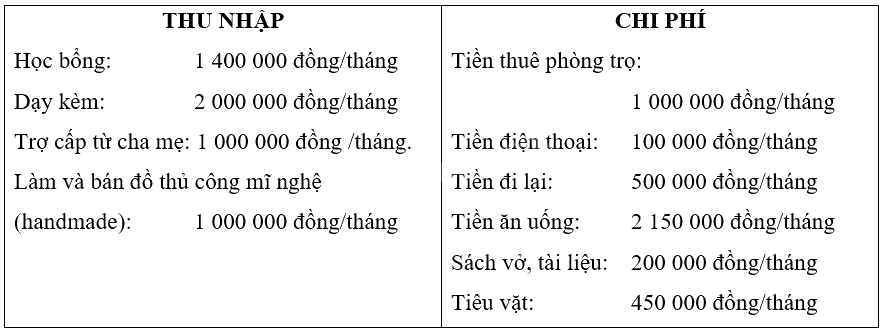
a) Hãy trình bày lại sổ tay của bạn Nam dưới dạng một bảng tính để tính toán tổng thu, tổng chi và cho biết bạn Nam còn dư hay thiếu tiền trong mỗi tháng.
b) Bạn có thể làm một bảng tính tương tự về thu chi của chính mình không?
Phương pháp giải:
‒ Lập bảng.
‒ Liên hệ thực tế.
Lời giải chi tiết:
a) Bảng ngân sách hằng tháng của bạn Nam:
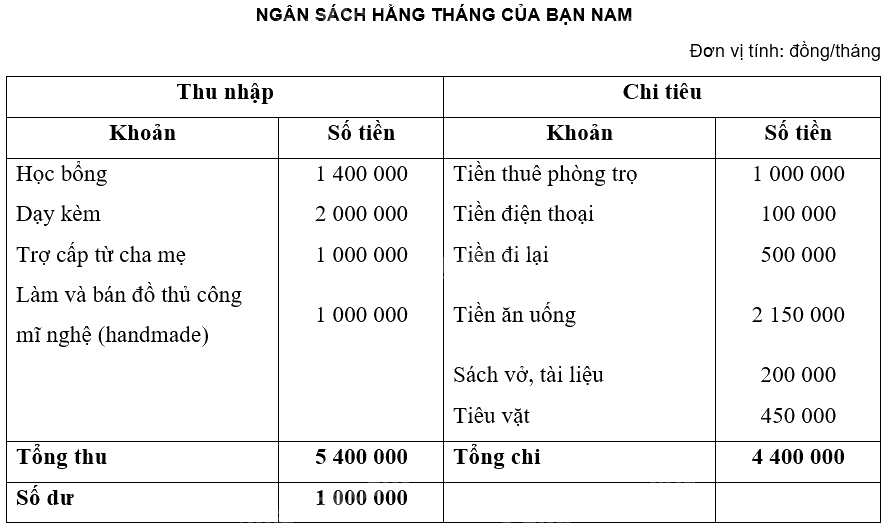
b) Bảng ngân sách hằng tháng của bản thân:
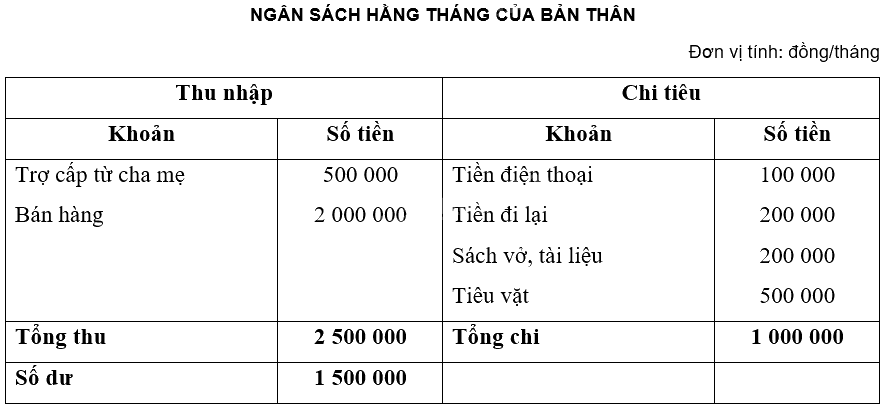
Trả lời câu hỏi Luyện tập 1 trang 44 Chuyên đề học tập Toán 12 Chân trời sáng tạo
Ông An đầu tư 1 tỉ đồng vào chứng chỉ quỹ tín dụng Q với lãi suất 10%/năm theo phương thức tính lãi kép trong thời gian 2 năm. Tính số tiền ông An nhận được sau 2 năm nếu kì trả lãi là 6 tháng, 3 tháng.
Phương pháp giải:
Giá trị cả vốn lẫn lãi sau \(n\) chu kì lãi kép: \({F_n} = P{\left( {1 + r} \right)^n}\) (với \(P\): vốn gốc, \(r\): lãi suất trên một kì hạn, \(n\): số kì hạn).
Lời giải chi tiết:
Với kì trả lãi 6 tháng, ta có: \(P = 1;r = \frac{6}{{12}}.10\% = 5\% ;n = 4\).
Số tiền ông An nhận được sau 2 năm là:
\(F = P{\left( {1 + r} \right)^4} = 1.{\left( {1 + 5\% } \right)^4} \approx 1,216\) (tỉ đồng).
Với kì trả lãi 3 tháng, ta có: \(P = 1;r = \frac{3}{{12}}.10\% = 2,5\% ;n = 8\).
Số tiền ông An nhận được sau 2 năm là:
\(F = P{\left( {1 + r} \right)^8} = 1.{\left( {1 + 2,5\% } \right)^8} \approx 1,218\) (tỉ đồng).
Trả lời câu hỏi Luyện tập 2 trang 44 Chuyên đề học tập Toán 12 Chân trời sáng tạo
Mỗi cổ phiếu của công ty X có giá bán 25 000 đồng và lợi nhuận trên mỗi cổ phiếu được công bố là 2 500 đồng/năm. Mỗi cổ phiếu của công ty Y có giá bán 10 000 đồng và lợi nhuận trên mỗi cổ phiếu được công bố là 500 đồng/năm.
a) Tính tỉ số phần trăm giữa giá bán và lợi nhuận trên mỗi cổ phiếu của công ty X và công ty Y (kết quả làm tròn đến hàng phần mười).
b) Nếu các nhà đầu tư có xu hướng thích mua các cổ phiếu được định giá thấp so với lợi nhuận thì cổ phiếu nào có giá trị đầu tư cao hơn?
Phương pháp giải:
Tính tỉ số phần trăm giữa giá bán và lợi nhuận.
Lời giải chi tiết:
a) Tỉ số phần trăm giữa giá bán và lợi nhuận trên mỗi cổ phiếu của công ty X là:
\(P/E = \frac{{25000}}{{2500}} = 1000\% \).
Tỉ số phần trăm giữa giá bán và lợi nhuận trên mỗi cổ phiếu của công ty Y là:
\(P/E = \frac{{10000}}{{500}} = 2000\% \).
b) Vì tỉ số phần trăm giữa giá bán và lợi nhuận trên mỗi cổ phiếu của công ty X nhỏ hơn tỉ số phần trăm giữa giá bán và lợi nhuận trên mỗi cổ phiếu của công ty Y nên cổ phiếu của công ty X có giá trị đầu tư cao hơn.
Trả lời câu hỏi Luyện tập 3 trang 44 Chuyên đề học tập Toán 12 Chân trời sáng tạo
Một công ty có ngân sách chi tiêu là \(T\) đồng, nếu giữ tiền mặt \({\rm{x}}\) đồng và đầu tư \(\left( {T - x} \right)\) đồng thì sẽ có lợi nhuận là:
\(f\left( x \right) = \frac{{a\left( {T - x} \right)}}{2} - \frac{{bT}}{x}\),
trong đó:
\(x\): số tiền mặt cần giữ, \(x \in \left( {0;T} \right]\);
\(a\): lãi suất đầu tư 28%;
\(b\): chi phí mỗi lần rút tiền mặt 20,5%.
Tìm \(x\) để \(f\left( x \right)\) đạt giá trị lớn nhất khi \(T = 12\) tỉ đồng.
Phương pháp giải:
Cách tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một khoảng hay nửa khoảng bằng đạo hàm:
‒ Lập bảng biến thiên của hàm số trên tập hợp đó.
‒ Căn cứ vào bảng biến thiên, kết luận giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của hàm số.
Lời giải chi tiết:
Xét hàm số \(f\left( x \right) = \frac{{28\% \left( {12 - x} \right)}}{2} - \frac{{12.20,5\% }}{x} = 0,14\left( {12 - x} \right) - \frac{{2,46}}{x} = 1,68 - 0,14x - \frac{{2,46}}{x}\) trên \(\left( {0;12} \right]\).
Ta có: \(f'\left( x \right) = - 0,14 + \frac{{2,46}}{{{x^2}}}\)
\(f'\left( x \right) = 0 \Leftrightarrow - 0,14 + \frac{{2,46}}{{{x^2}}} = 0 \Leftrightarrow {x^2} = \frac{{123}}{7} \Leftrightarrow x = \frac{{\sqrt {861} }}{7}\) hoặc \(x = - \frac{{\sqrt {861} }}{7}\) (loại).
Bảng biến thiên của hàm số trên nửa khoảng \(\left( {0;12} \right]\):
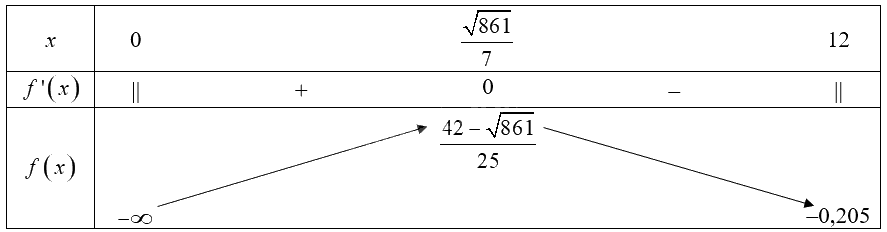
Từ bảng biến thiên, ta thấy \(\mathop {\max }\limits_{\left( {0;12} \right]} f\left( x \right) = f\left( {\frac{{\sqrt {861} }}{7}} \right) = \frac{{42 - \sqrt {861} }}{{25}}\).
Vậy \(x = \frac{{\sqrt {861} }}{7} \approx 4,2\) (tỉ đồng) để \(f\left( x \right)\) đạt giá trị lớn nhất.
Trả lời câu hỏi Luyện tập 4 trang 44 Chuyên đề học tập Toán 12 Chân trời sáng tạo
Ông Sơn tạo ra một dòng tiền bằng cách cuối mỗi năm đều gửi tiết kiệm 100 triệu đồng vào ngân hàng với lãi suất 9%/năm theo phương thức tính lãi kép với kì hạn 1 năm. Hỏi sau bao lâu thì ông Sơn có đủ 2 tỉ đồng để mua một mảnh đất?
Phương pháp giải:
Sử dụng công thức: \(n = \frac{{\ln \left( {\frac{{F{\rm{r}}}}{A} + 1} \right)}}{{\ln \left( {1 + r} \right)}}\) (với \(F\): số tiền người đó thu được ở cuối dòng tiền, \(A\): số tiền gửi từng kì hạn, \(r\): lãi suất trên một kì hạn, \(n\): số kì hạn).
Lời giải chi tiết:
Ta có: \(F = 2,r = 9\% ,A = 0,1\).
\(n = \frac{{\ln \left( {\frac{{F{\rm{r}}}}{A} + 1} \right)}}{{\ln \left( {1 + r} \right)}} = \frac{{\ln \left( {\frac{{2.9\% }}{{0,1}} + 1} \right)}}{{\ln \left( {1 + 9\% } \right)}} \approx 11,95\).
Vậy sau 12 năm thì ông Sơn có đủ 2 tỉ đồng để mua một mảnh đất.
Trả lời câu hỏi Hoạt động 2 trang 45 Chuyên đề học tập Toán 12 Chân trời sáng tạo
Bạn Nam là một sinh viên năm nhất thuê nhà trọ để học đại học. Dưới đây là bảng thu chi trong sổ tay của bạn Nam.
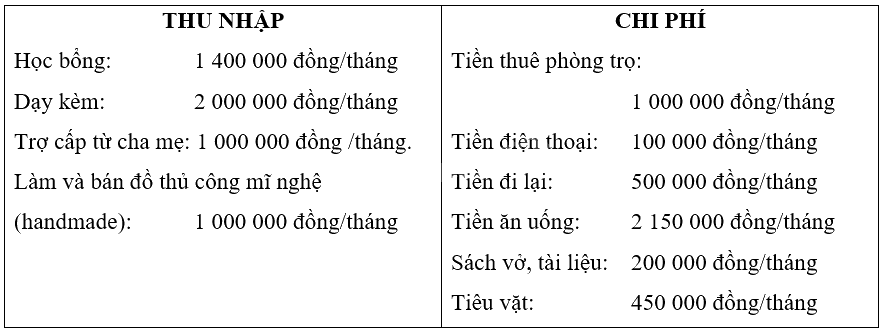
a) Hãy trình bày lại sổ tay của bạn Nam dưới dạng một bảng tính để tính toán tổng thu, tổng chi và cho biết bạn Nam còn dư hay thiếu tiền trong mỗi tháng.
b) Bạn có thể làm một bảng tính tương tự về thu chi của chính mình không?
Phương pháp giải:
‒ Lập bảng.
‒ Liên hệ thực tế.
Lời giải chi tiết:
a) Bảng ngân sách hằng tháng của bạn Nam:
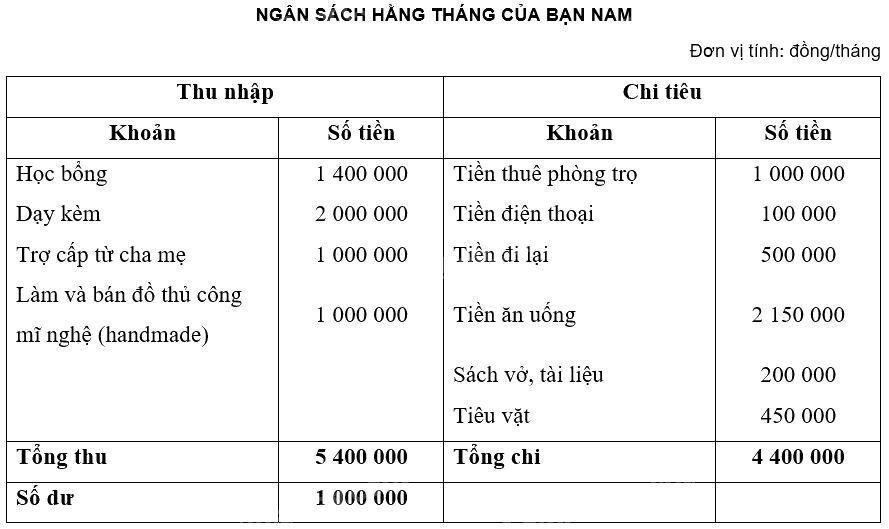
b) Bảng ngân sách hằng tháng của bản thân:
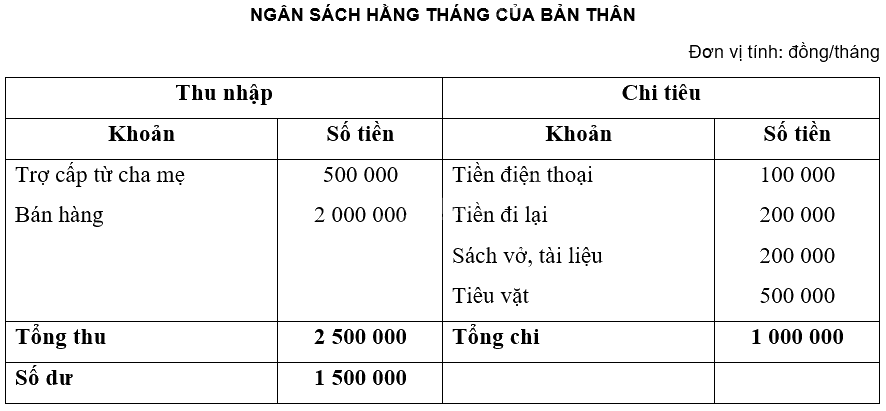
Mục 2 của Chuyên đề học tập Toán 12 - Chân trời sáng tạo thường tập trung vào một chủ đề cụ thể, đòi hỏi học sinh phải nắm vững lý thuyết và kỹ năng giải bài tập liên quan. Việc giải các bài tập trang 41, 42, 43, 44, 45 là bước quan trọng để củng cố kiến thức và chuẩn bị cho các kỳ thi sắp tới.
Để hiểu rõ hơn về Mục 2, trước tiên chúng ta cần xác định nội dung chính mà chuyên đề này hướng đến. Thông thường, Mục 2 sẽ đi sâu vào một trong các chủ đề sau:
Để giải các bài tập trong Mục 2 trang 41, 42, 43, 44, 45 một cách hiệu quả, các em cần áp dụng các phương pháp sau:
Dưới đây là phần giải chi tiết các bài tập trang 41, 42, 43, 44, 45 của Mục 2 Chuyên đề học tập Toán 12 - Chân trời sáng tạo. Chúng tôi sẽ trình bày từng bài tập một cách rõ ràng, dễ hiểu, kèm theo các bước giải cụ thể và giải thích chi tiết.
(Nội dung bài tập và lời giải chi tiết)
(Nội dung bài tập và lời giải chi tiết)
(Nội dung bài tập và lời giải chi tiết)
(Nội dung bài tập và lời giải chi tiết)
(Nội dung bài tập và lời giải chi tiết)
Trong quá trình giải bài tập, các em cần lưu ý những điều sau:
Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!