Chào mừng các em học sinh đến với lời giải chi tiết bài 9 trang 23 Chuyên đề học tập Toán 12 - Chân trời sáng tạo. Bài viết này sẽ cung cấp cho các em phương pháp giải bài tập một cách nhanh chóng và hiệu quả.
Giaitoan.edu.vn luôn đồng hành cùng các em trong quá trình học tập, giúp các em nắm vững kiến thức và đạt kết quả tốt nhất.
Hàm lượng protein, lipid và glucid (tính theo gam) trong 100 g mỗi loại thực phẩm A và B được cho bởi bảng sau: Từ hai loại thực phẩm A và B, người ta muốn tạo ra một lượng thực phẩm chứa ít nhất 480 g protein, 90 g lipid và 2400 g glucid. Biết rằng một kilôgam mỗi loại thực phẩm A và B có giá lần lượt là 80 nghìn đồng, 100 nghìn đồng. Cần chọn bao nhiêu kilôgam mỗi loại thực phẩm A và B để chi phí thấp nhất?
Đề bài
Hàm lượng protein, lipid và glucid (tính theo gam) trong 100 g mỗi loại thực phẩm A và B được cho bởi bảng sau:

Từ hai loại thực phẩm A và B, người ta muốn tạo ra một lượng thực phẩm chứa ít nhất 480 g protein, 90 g lipid và 2400 g glucid. Biết rằng một kilôgam mỗi loại thực phẩm A và B có giá lần lượt là 80 nghìn đồng, 100 nghìn đồng. Cần chọn bao nhiêu kilôgam mỗi loại thực phẩm A và B để chi phí thấp nhất?
Phương pháp giải - Xem chi tiết
Bước 1: Đặt hai ẩn biểu thị hai đại lượng chưa biết (cần tìm). Viết điều kiện có nghĩa cho các ẩn đó.
Bước 2: Từ dữ kiện của bài toán, viết biểu thức biểu thị đại lượng cần tìm giá trị tối ưu và các bất phương trình bậc nhất đối với hai ẩn trên. Từ đó phát biểu bài toán quy hoạch tuyến tính nhận được.
Bước 3: Giải bài toán quy hoạch tuyến tính và trả lời.
Lời giải chi tiết
Gọi \(x,y\) (\(x \ge 0,y \ge 0\), tính theo 100g) lần lượt là khối lượng thực phẩm A và B cần chọn.
Thực phẩm chứa ít nhất 480 g protein nên ta có \(24x + 8y \ge 480\) hay \(3x + y - 60 \ge 0\).
Thực phẩm chứa ít nhất 90 g lipid nên ta có \(3x + 2y \ge 90\) hay \(3x + 2y - 90 \ge 0\).
Thực phẩm chứa ít nhất 2400 g glucid nên ta có \(60x + 80y \ge 2400\) hay \(3x + 4y - 120 \ge 0\).
Khối lượng thực phẩm cần mua là \(F = 8x + 10y\) (nghìn đồng).
Từ đó, ta cần giải bài toán quy hoạch tuyến tính: \(F = 8x + 10y \to \min \) với ràng buộc \(\left\{ \begin{array}{l}3x + y - 60 \ge 0\\3x + 2y - 90 \ge 0\\3x + 4y - 120 \ge 0\\x \ge 0\\y \ge 0\end{array} \right.\)
Tập phương án \({\Omega }\) của bài toán là miền không gạch (không là miền đa giác).
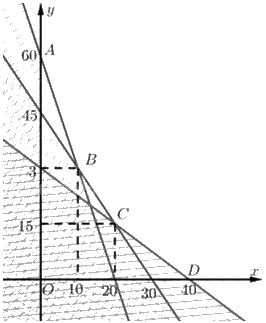
Ta có \(A\left( {0;60} \right),D\left( {40;0} \right)\).
Toạ độ \(B\) là nghiệm của hệ \(\left\{ \begin{array}{l}3x + y = 60\\3x + 2y = 90\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 10\\y = 30\end{array} \right.\). Vậy \(B\left( {10;30} \right)\).
Toạ độ \(C\) là nghiệm của hệ \(\left\{ \begin{array}{l}3x + 4y = 120\\3x + 2y = 90\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 20\\y = 15\end{array} \right.\). Vậy \(C\left( {20;15} \right)\).
Giá trị của biểu thức \(F\) tại các đỉnh của \({\Omega }\):
\(F\left( {0;60} \right) = 600;F\left( {10;30} \right) = 380;F\left( {20;15} \right) = 310;F\left( {40;0} \right) = 320\)
Do đó: \(\mathop {\min }\limits_{\Omega } F = F\left( {20;15} \right) = 310\).
Vậy cần chọn \(20.100 = 2000g = 2kg\) thực phẩm A và \(15.100 = 1500g = 1,5kg\) thực phẩm B để chi phí thấp nhất.
Bài 9 trang 23 Chuyên đề học tập Toán 12 - Chân trời sáng tạo thuộc chương trình học Toán 12, tập trung vào việc ôn tập và củng cố kiến thức về đạo hàm. Bài tập này yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế, rèn luyện kỹ năng tính toán và tư duy logic.
Bài 9 trang 23 thường bao gồm các dạng bài tập sau:
Để giải quyết bài 9 trang 23 Chuyên đề học tập Toán 12 - Chân trời sáng tạo một cách hiệu quả, học sinh cần nắm vững các kiến thức và kỹ năng sau:
Dưới đây là lời giải chi tiết cho từng phần của bài 9 trang 23 Chuyên đề học tập Toán 12 - Chân trời sáng tạo:
f'(x) = 3x^2 - 4x + 5
g'(x) = 4x^3 - 8x = 4x(x^2 - 2)
g'(x) = 0 khi x = 0, x = √2, x = -√2
Xét dấu g'(x) để xác định cực trị...
h'(x) = -2/(x-1)^2
Tiệm cận đứng: x = 1
Tiệm cận ngang: y = 1
...
Ví dụ 1: Tính đạo hàm của hàm số y = sin(2x)
y' = cos(2x) * 2 = 2cos(2x)
Ví dụ 2: Tìm cực trị của hàm số y = x^3 - 3x
y' = 3x^2 - 3
y' = 0 khi x = 1, x = -1
...
Để củng cố kiến thức, các em có thể tự giải các bài tập sau:
Bài 9 trang 23 Chuyên đề học tập Toán 12 - Chân trời sáng tạo là một bài tập quan trọng giúp học sinh ôn tập và củng cố kiến thức về đạo hàm. Hy vọng với lời giải chi tiết và phương pháp giải bài tập được trình bày trong bài viết này, các em sẽ tự tin hơn khi giải quyết các bài toán tương tự.
Giaitoan.edu.vn luôn sẵn sàng hỗ trợ các em trong quá trình học tập. Chúc các em học tốt!