Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 2 trang 36, 37 Chuyên đề học tập Toán 12 - Chân trời sáng tạo. Tại giaitoan.edu.vn, chúng tôi cung cấp các bài giải được trình bày rõ ràng, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải quyết các bài toán tương tự.
Chúng tôi hiểu rằng việc học toán đôi khi có thể gặp nhiều khó khăn. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của chúng tôi đã biên soạn các lời giải chi tiết, kèm theo các lưu ý quan trọng để giúp các em hiểu sâu sắc hơn về nội dung bài học.
Công ty A vay của ngân hàng B với hợp đồng vay như sau: Số tiền vay là 100 triệu đồng, thời hạn vay 12 tháng, lãi suất cho vay 9%/năm. Tiền lãi tính theo dư nợ ban đầu. a) Tính tổng số tiền gốc và lãi mà công ty A phải trả cho ngân hàng B vào cuối kì vay. b) Nếu hợp đồng vay yêu cầu tiền gốc phải trả đều mỗi tháng, tiền lãi tính theo dư nợ giảm dần. Tính số tiền gốc và lãi mà công ty A phải trả mỗi tháng và tổng số tiền gốc và lãi công ty đã trả tổng cộng cho hợp đồng vay nói trên.
Trả lời câu hỏi Vận dụng 2 trang 37 Chuyên đề học tập Toán 12 Chân trời sáng tạo
Bác Hà vay của ngân hàng ABC 500 triệu đồng để mua ô tô với hợp đồng vay như sau: Thời hạn vay 7 năm, gốc trả đều hằng tháng theo số tháng vay, lãi trả hằng tháng với lãi suất 12%/năm tính theo dư nợ giảm dần. Tính:
a) Số tiền gốc và lãi mà bác Hà phải trả ở tháng thứ \(k\left( {k = 1,2,...,84} \right)\).
b) Tổng số tiền gốc và lãi mà bác Hà phải trả sau 84 tháng.
Phương pháp giải:
Lãi đơn: \({I_n} = P.r.n\) (với \(P\): vốn gốc, \(r\): lãi suất trên một kì hạn, \(n\): số kì hạn).
Lời giải chi tiết:
a) Mỗi tháng số tiền gốc phải trả là: \(\frac{{500}}{{84}}\) (triệu đồng).
Dư nợ gốc còn lại ở tháng thứ \(k\) là: \(500 - \frac{{500}}{{84}}.\left( {k - 1} \right) = 500.\frac{{85 - k}}{{84}}\) (triệu đồng).
Lãi suất trên một tháng là: \(r = \frac{1}{{12}}.12\% = 1\% \)
Số tiền lãi phải trả ở tháng thứ \(k\) là: \({I_k} = 500.\frac{{85 - k}}{{84}}.1\% \) (triệu đồng).
Số tiền gốc và lãi phải trả ở tháng thứ \(k\) là: \({F_k} = \frac{{500}}{{84}}.k + \left( {85 - k} \right)\frac{{500}}{{84}}.1\% \) (triệu đồng).
b) Số tiền gốc phải trả sau 84 tháng là: 500 (triệu đồng).
Tổng số tiền lãi phải trả sau 84 tháng là:
\(\begin{array}{l}I = 500.\frac{{85 - 1}}{{84}}.1\% + 500.\frac{{85 - 2}}{{84}}.1\% + ... + 500.\frac{{85 - 84}}{{84}}.1\% \\ = 500.\frac{{84}}{{84}}.1\% + 500.\frac{{83}}{{84}}.1\% + ... + 500.\frac{1}{{84}}.1\% \end{array}\)
\( = \frac{{500}}{{84}}.1\% \left( {1 + 2 + ... + 84} \right) = \frac{{500}}{{84}}.1\% .\frac{{84\left( {1 + 84} \right)}}{2} = 212,5\) (triệu đồng).
Tổng số tiền gốc và lãi bác Năm phải trả sau 84 tháng là \(500 + 212,5 = 712,5\) (triệu đồng).
Trả lời câu hỏi Luyện tập 2 trang 37 Chuyên đề học tập Toán 12 Chân trời sáng tạo
Công ty A vay của ngân hàng B với hợp đồng vay như sau: Số tiền vay là 100 triệu đồng, thời hạn vay 12 tháng, lãi suất cho vay 9%/năm. Tiền lãi tính theo dư nợ ban đầu.
a) Tính tổng số tiền gốc và lãi mà công ty A phải trả cho ngân hàng B vào cuối kì vay.
b) Nếu hợp đồng vay yêu cầu tiền gốc phải trả đều mỗi tháng, tiền lãi tính theo dư nợ giảm dần. Tính số tiền gốc và lãi mà công ty A phải trả mỗi tháng và tổng số tiền gốc và lãi công ty đã trả tổng cộng cho hợp đồng vay nói trên.
Phương pháp giải:
‒ Lãi đơn: \({I_n} = P.r.n\) (với \(P\): vốn gốc, \(r\): lãi suất trên một kì hạn, \(n\): số kì hạn).
‒ Giá trị cả vốn lẫn lãi sau \(n\) chu kì lãi đơn: \({F_n} = P\left( {1 + n{\rm{r}}} \right)\) (với \(P\): vốn gốc, \(r\): lãi suất trên một kì hạn, \(n\): số kì hạn).
Lời giải chi tiết:
a) Do tiền lãi tính theo dư nợ ban đầu nên công ty A sẽ trả nợ ngân hàng B theo phương thức lãi đơn.
Ta có: \(P = 100,r = 9\% ,n = 1\).
Tổng số tiền gốc và lãi mà công ty A phải trả cho ngân hàng B vào cuối kì vay là:
\(100\left( {1 + 9\% } \right) = 109\) (triệu đồng).
b) Áp dụng công thức lãi đơn cho từng tháng, theo hợp đồng vay ta có bảng tính sau:
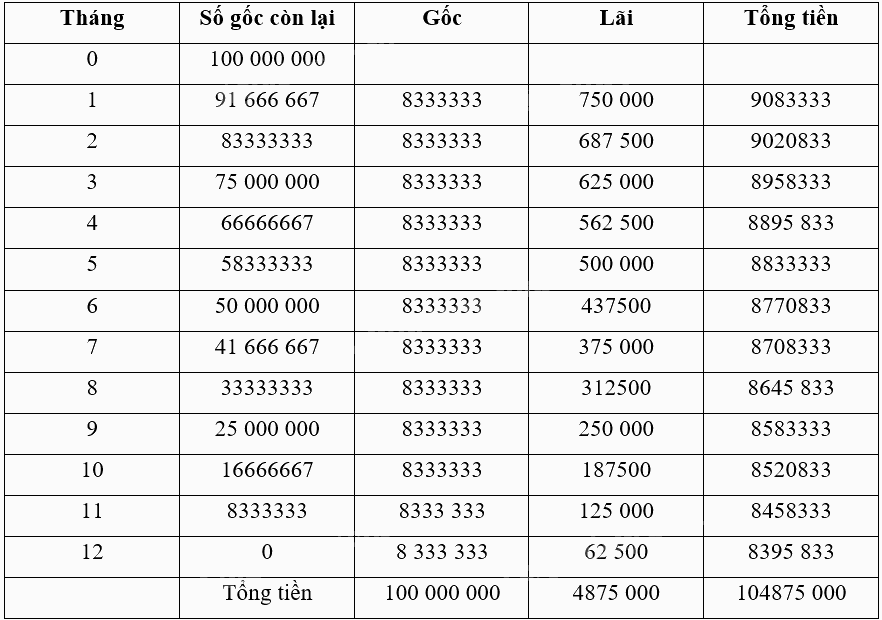
Trả lời câu hỏi Vận dụng 2 trang 37 Chuyên đề học tập Toán 12 Chân trời sáng tạo
Bác Hà vay của ngân hàng ABC 500 triệu đồng để mua ô tô với hợp đồng vay như sau: Thời hạn vay 7 năm, gốc trả đều hằng tháng theo số tháng vay, lãi trả hằng tháng với lãi suất 12%/năm tính theo dư nợ giảm dần. Tính:
a) Số tiền gốc và lãi mà bác Hà phải trả ở tháng thứ \(k\left( {k = 1,2,...,84} \right)\).
b) Tổng số tiền gốc và lãi mà bác Hà phải trả sau 84 tháng.
Phương pháp giải:
Lãi đơn: \({I_n} = P.r.n\) (với \(P\): vốn gốc, \(r\): lãi suất trên một kì hạn, \(n\): số kì hạn).
Lời giải chi tiết:
a) Mỗi tháng số tiền gốc phải trả là: \(\frac{{500}}{{84}}\) (triệu đồng).
Dư nợ gốc còn lại ở tháng thứ \(k\) là: \(500 - \frac{{500}}{{84}}.\left( {k - 1} \right) = 500.\frac{{85 - k}}{{84}}\) (triệu đồng).
Lãi suất trên một tháng là: \(r = \frac{1}{{12}}.12\% = 1\% \)
Số tiền lãi phải trả ở tháng thứ \(k\) là: \({I_k} = 500.\frac{{85 - k}}{{84}}.1\% \) (triệu đồng).
Số tiền gốc và lãi phải trả ở tháng thứ \(k\) là: \({F_k} = \frac{{500}}{{84}}.k + \left( {85 - k} \right)\frac{{500}}{{84}}.1\% \) (triệu đồng).
b) Số tiền gốc phải trả sau 84 tháng là: 500 (triệu đồng).
Tổng số tiền lãi phải trả sau 84 tháng là:
\(\begin{array}{l}I = 500.\frac{{85 - 1}}{{84}}.1\% + 500.\frac{{85 - 2}}{{84}}.1\% + ... + 500.\frac{{85 - 84}}{{84}}.1\% \\ = 500.\frac{{84}}{{84}}.1\% + 500.\frac{{83}}{{84}}.1\% + ... + 500.\frac{1}{{84}}.1\% \end{array}\)
\( = \frac{{500}}{{84}}.1\% \left( {1 + 2 + ... + 84} \right) = \frac{{500}}{{84}}.1\% .\frac{{84\left( {1 + 84} \right)}}{2} = 212,5\) (triệu đồng).
Tổng số tiền gốc và lãi bác Năm phải trả sau 84 tháng là \(500 + 212,5 = 712,5\) (triệu đồng).
Trả lời câu hỏi Luyện tập 2 trang 37 Chuyên đề học tập Toán 12 Chân trời sáng tạo
Công ty A vay của ngân hàng B với hợp đồng vay như sau: Số tiền vay là 100 triệu đồng, thời hạn vay 12 tháng, lãi suất cho vay 9%/năm. Tiền lãi tính theo dư nợ ban đầu.
a) Tính tổng số tiền gốc và lãi mà công ty A phải trả cho ngân hàng B vào cuối kì vay.
b) Nếu hợp đồng vay yêu cầu tiền gốc phải trả đều mỗi tháng, tiền lãi tính theo dư nợ giảm dần. Tính số tiền gốc và lãi mà công ty A phải trả mỗi tháng và tổng số tiền gốc và lãi công ty đã trả tổng cộng cho hợp đồng vay nói trên.
Phương pháp giải:
‒ Lãi đơn: \({I_n} = P.r.n\) (với \(P\): vốn gốc, \(r\): lãi suất trên một kì hạn, \(n\): số kì hạn).
‒ Giá trị cả vốn lẫn lãi sau \(n\) chu kì lãi đơn: \({F_n} = P\left( {1 + n{\rm{r}}} \right)\) (với \(P\): vốn gốc, \(r\): lãi suất trên một kì hạn, \(n\): số kì hạn).
Lời giải chi tiết:
a) Do tiền lãi tính theo dư nợ ban đầu nên công ty A sẽ trả nợ ngân hàng B theo phương thức lãi đơn.
Ta có: \(P = 100,r = 9\% ,n = 1\).
Tổng số tiền gốc và lãi mà công ty A phải trả cho ngân hàng B vào cuối kì vay là:
\(100\left( {1 + 9\% } \right) = 109\) (triệu đồng).
b) Áp dụng công thức lãi đơn cho từng tháng, theo hợp đồng vay ta có bảng tính sau:
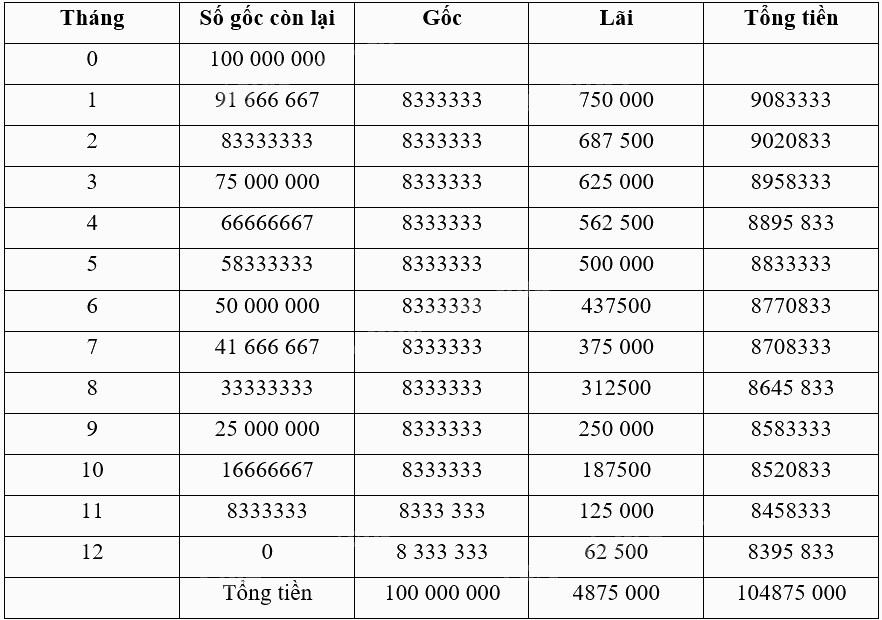
Mục 2 của Chuyên đề học tập Toán 12 - Chân trời sáng tạo thường tập trung vào một chủ đề cụ thể trong chương trình. Trang 36 và 37 thường chứa các bài tập vận dụng và mở rộng kiến thức đã học. Việc giải các bài tập này không chỉ giúp học sinh củng cố lý thuyết mà còn rèn luyện kỹ năng giải quyết vấn đề, một kỹ năng vô cùng quan trọng trong học tập và cuộc sống.
Để giải quyết hiệu quả các bài tập trang 36, học sinh cần nắm vững các khái niệm và định lý liên quan đến chủ đề đang xét. Thông thường, các bài tập ở trang này sẽ yêu cầu học sinh:
Trang 37 thường chứa các bài tập nâng cao, đòi hỏi học sinh phải có khả năng tư duy logic và sáng tạo. Các bài tập này có thể yêu cầu học sinh:
Để giải bài tập mục 2 trang 36, 37 Chuyên đề học tập Toán 12 - Chân trời sáng tạo một cách hiệu quả, học sinh nên:
Bài tập: (Giả sử một bài tập cụ thể từ trang 36 hoặc 37). Giải bài tập này bằng cách áp dụng các kiến thức và phương pháp đã trình bày ở trên.
Lời giải: (Giải chi tiết bài tập, trình bày các bước giải rõ ràng và dễ hiểu).
Khi giải bài tập Toán 12, học sinh cần lưu ý:
Toán 12 là một môn học quan trọng, đóng vai trò then chốt trong việc chuẩn bị cho kỳ thi tốt nghiệp THPT và xét tuyển đại học. Việc nắm vững kiến thức Toán 12 sẽ giúp học sinh tự tin hơn trong quá trình học tập và làm việc sau này.
Hy vọng rằng với lời giải chi tiết và phương pháp giải bài tập hiệu quả mà giaitoan.edu.vn cung cấp, các em học sinh sẽ tự tin hơn trong việc học tập và giải quyết các bài tập Toán 12. Chúc các em học tập tốt và đạt kết quả cao!