Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho bài tập Toán 12. Bài viết này sẽ hướng dẫn bạn giải bài 5 trang 14 thuộc Chuyên đề học tập Toán 12 - Chân trời sáng tạo một cách nhanh chóng và hiệu quả.
Chúng tôi hiểu rằng việc giải các bài tập Toán đôi khi có thể gặp khó khăn. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của chúng tôi đã biên soạn lời giải chi tiết, kèm theo các bước giải thích rõ ràng, giúp bạn nắm vững kiến thức và kỹ năng cần thiết.
Hàm lượng các vi chất (chất vi lượng) calcium, phosphorus và iron chứa trong 100 g hai loại thực phẩm X và Y được cho ở bảng sau: Từ hai loại thực phẩm X và Y, người ta muốn tạo ra một lượng thực phẩm hỗn hợp chứa ít nhất 2000 mg calcium, 3000 mg phosphorus, 48 mg iron. Cần chọn bao nhiêu gam mỗi loại thực phẩm X và Y sao cho lượng thực phẩm hỗn hợp có khối lượng nhỏ nhất?
Đề bài
Hàm lượng các vi chất (chất vi lượng) calcium, phosphorus và iron chứa trong 100 g hai loại thực phẩm X và Y được cho ở bảng sau:

Từ hai loại thực phẩm X và Y, người ta muốn tạo ra một lượng thực phẩm hỗn hợp chứa ít nhất 2000 mg calcium, 3000 mg phosphorus, 48 mg iron. Cần chọn bao nhiêu gam mỗi loại thực phẩm X và Y sao cho lượng thực phẩm hỗn hợp có khối lượng nhỏ nhất?
Phương pháp giải - Xem chi tiết
Bước 1: Đặt hai ẩn biểu thị hai đại lượng chưa biết (cần tìm). Viết điều kiện có nghĩa cho các ẩn đó.
Bước 2: Từ dữ kiện của bài toán, viết biểu thức biểu thị đại lượng cần tìm giá trị tối ưu và các bất phương trình bậc nhất đối với hai ẩn trên. Từ đó phát biểu bài toán quy hoạch tuyến tính nhận được.
Bước 3: Giải bài toán quy hoạch tuyến tính và trả lời.
Lời giải chi tiết
Gọi \(x,y\) (\(x \ge 0,y \ge 0\), tính theo 100g) lần lượt là khối lượng thực phẩm X và Y cần chọn.
Cần cung cấp ít nhất 2000 mg calcium nên ta có \(200x + 500y \ge 2000\) hay \(2x + 5y - 20 \ge 0\).
Cần cung cấp ít nhất 3000 mg phosphorus nên ta có \(600x + 300y \ge 3000\) hay \(2x + y - 10 \ge 0\).
Cần cung cấp ít nhất 48 mg iron nên ta có \(8x + 6y \ge 48\) hay \(4x + 3y - 24 \ge 0\).
Khối lượng thực phẩm cần mua là \(F = 100\left( {x + y} \right)\) (nghìn đồng).
Từ đó, ta cần giải bài toán quy hoạch tuyến tính: \(F = 100\left( {x + y} \right) \to \min \) với ràng buộc \(\left\{ \begin{array}{l}2x + 5y - 20 \ge 0\\2x + y - 10 \ge 0\\4x + 3y - 24 \ge 0\\x \ge 0\\y \ge 0\end{array} \right.\)
Tập phương án \({\Omega }\) của bài toán là miền không gạch (không là miền đa giác).
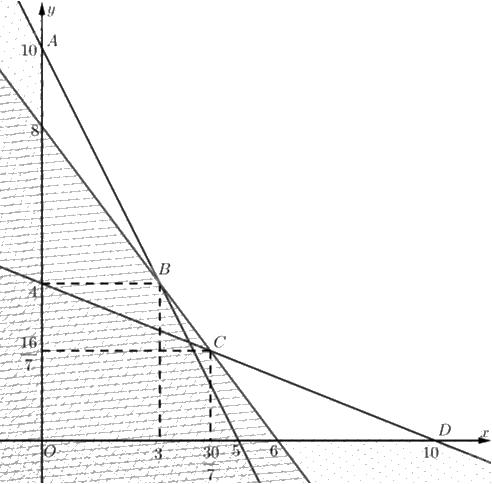
Ta có \(A\left( {0;10} \right),D\left( {10;0} \right)\).
Toạ độ \(B\) là nghiệm của hệ \(\left\{ \begin{array}{l}2x + y = 10\\4x + 3y = 24\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 3\\y = 4\end{array} \right.\). Vậy \(B\left( {3;4} \right)\).
Toạ độ \(C\) là nghiệm của hệ \(\left\{ \begin{array}{l}2x+5y=20\\4x+3y=24\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x=\frac{30}{7}\\y=\frac{16}{7}\end{array} \right.\). Vậy \(C\left( {\frac{{30}}{7};\frac{{16}}{7}} \right)\).
Giá trị của biểu thức \(F\) tại các đỉnh của \({\Omega }\):
\(F\left( {0;10} \right) = 1000;F\left( {3;4} \right) = 700;F\left( {\frac{{30}}{7};\frac{{16}}{7}} \right) = \frac{{4600}}{7};F\left( {10;0} \right) = 1000\)
Do đó: \(\mathop {\min }\limits_{\Omega } F = F\left( {\frac{{30}}{7};\frac{{16}}{7}} \right) = \frac{{4600}}{7}\).
Vậy cần mua \(\frac{{30}}{7}.100g = \frac{{3000}}{7}g \approx 429g\) thực phẩm X và \(\frac{{16}}{7}.100g = \frac{{1600}}{7}g \approx 229g\) thực phẩm Y để thực phẩm hỗn hợp có khối lượng nhỏ nhất.
Bài 5 trang 14 Chuyên đề học tập Toán 12 - Chân trời sáng tạo thường tập trung vào một trong các chủ đề chính của chương trình, ví dụ như đạo hàm, tích phân, hoặc các bài toán về hình học không gian. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản, công thức liên quan và kỹ năng giải toán.
Trước khi bắt đầu giải bài, điều quan trọng nhất là phải đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Điều này bao gồm việc xác định các dữ kiện đã cho, các đại lượng cần tìm và các điều kiện ràng buộc. Việc phân tích đề bài một cách cẩn thận sẽ giúp bạn tránh được những sai sót không đáng có và tìm ra hướng giải quyết phù hợp.
Để minh họa, chúng ta sẽ giả sử bài 5 trang 14 yêu cầu tính đạo hàm của một hàm số phức tạp. Dưới đây là các bước giải bài toán này:
Kiến thức được học trong bài 5 trang 14 có ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau, bao gồm:
Bài 5 trang 14 Chuyên đề học tập Toán 12 - Chân trời sáng tạo là một bài tập quan trọng giúp học sinh củng cố kiến thức và rèn luyện kỹ năng giải toán. Bằng cách phân tích đề bài, áp dụng các quy tắc đạo hàm cơ bản và luyện tập thường xuyên, bạn có thể giải quyết bài toán này một cách hiệu quả và đạt kết quả tốt nhất.