Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài 3 trang 64 Chuyên đề học tập Toán 12 - Chân trời sáng tạo. Bài viết này cung cấp đáp án đầy đủ, phương pháp giải rõ ràng, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Chúng tôi luôn cố gắng cung cấp nội dung chất lượng, dễ hiểu, phù hợp với chương trình học Toán 12 hiện hành.
Một túi chứa 2 viên bi xanh và 8 viên bi đỏ có cùng kích thước và khối lượng. Chọn ra ngẫu nhiên đồng thời 2 viên bi từ túi. Gọi \(Y\) là số viên bi đỏ trong 2 viên bi được chọn ra. a) Hãy tìm tập các giá trị có thể của \(Y\). b) Lập bảng phân bố xác suất của \(Y\). c) Tính kì vọng và phương sai của \(Y\).
Đề bài
Một túi chứa 2 viên bi xanh và 8 viên bi đỏ có cùng kích thước và khối lượng. Chọn ra ngẫu nhiên đồng thời 2 viên bi từ túi. Gọi \(Y\) là số viên bi đỏ trong 2 viên bi được chọn ra.
a) Hãy tìm tập các giá trị có thể của \(Y\).
b) Lập bảng phân bố xác suất của \(Y\).
c) Tính kì vọng và phương sai của \(Y\).
Phương pháp giải - Xem chi tiết
Giả sử biến ngẫu nhiên rời rạc \(X\) có bảng phân bố xác suất như sau:
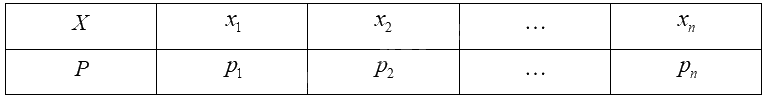
Kì vọng của \(X\) được tính bởi công thức: \(E\left( X \right) = {x_1}{p_1} + {x_2}{p_2} + ... + {x_n}{p_n}\).
Phương sai của \(X\) được tính bởi công thức: \(V\left( X \right) = x_1^2{p_1} + x_2^2{p_2} + ... + x_n^2{p_n} - {\left[ {E\left( X \right)} \right]^2}\).
Lời giải chi tiết
a) Trong 2 viên bi được chọn ra, có thể chọn được 2 viên bi xanh, 1 viên bi đỏ và 1 viên bi xanh, hoặc 2 viên bi đỏ. Vậy tập các giá trị có thể của \(Y\) là: \(\left\{ {0;1;2} \right\}\).
b) Chọn ra ngẫu nhiên đồng thời 2 viên bi từ túi có: \({C}_{10}^2\) cách.
Chọn ra 2 viên bi xanh có: \({C}_2^2\) cách. Vậy \(P\left( {Y = 0} \right) = \frac{{{C}_2^2}}{{{C}_{10}^2}} = \frac{1}{{45}}\).
Chọn ra 1 viên bi đỏ và 1 viên bi xanh có: \({C}_2^1.{C}_8^1\) cách. Vậy \(P\left( {Y = 1} \right) = \frac{{{C}_2^1.{C}_8^1}}{{{C}_{10}^2}} = \frac{{16}}{{45}}\).
Chọn ra 2 viên bi đỏ có: \({C}_8^2\) cách. Vậy \(P\left( {Y = 3} \right) = \frac{{{C}_8^2}}{{{C}_{10}^2}} = \frac{{28}}{{45}}\).
Bảng phân bố xác suất của \(Y\):

c) Kì vọng của \(Y\) là: \(E\left( Y \right) = 0.\frac{1}{{45}} + 1.\frac{{16}}{{45}} + 2.\frac{{28}}{{45}} = 1,6\).
Phương sai của \(Y\) là: \(V\left( Y \right) = {0^2}.\frac{1}{{45}} + {1^2}.\frac{{16}}{{45}} + {2^2}.\frac{{28}}{{45}} - {1,6^2} = \frac{{64}}{{225}}\).
Bài 3 trang 64 Chuyên đề học tập Toán 12 - Chân trời sáng tạo thuộc chương trình học về đạo hàm và ứng dụng của đạo hàm. Bài tập này thường tập trung vào việc vận dụng các kiến thức về đạo hàm để giải quyết các bài toán thực tế, liên quan đến sự biến thiên của hàm số, tìm cực trị, và các ứng dụng khác.
Bài 3 thường bao gồm các dạng bài tập sau:
Để giải quyết bài 3 trang 64 Chuyên đề học tập Toán 12 - Chân trời sáng tạo một cách hiệu quả, bạn cần nắm vững các bước sau:
Bài toán: Cho hàm số y = x3 - 3x2 + 2. Tìm các điểm cực trị của hàm số.
Giải:
Để đạt kết quả tốt nhất khi giải bài 3 trang 64 Chuyên đề học tập Toán 12 - Chân trời sáng tạo, bạn nên:
Sách giáo khoa Toán 12 - Chân trời sáng tạo
Các trang web học toán online uy tín như giaitoan.edu.vn
Bài 3 trang 64 Chuyên đề học tập Toán 12 - Chân trời sáng tạo là một bài tập quan trọng giúp học sinh củng cố kiến thức về đạo hàm và ứng dụng của đạo hàm. Hy vọng với hướng dẫn chi tiết và các ví dụ minh họa trên, bạn sẽ giải quyết bài tập này một cách dễ dàng và hiệu quả.