Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 12 Chân trời sáng tạo tại giaitoan.edu.vn. Chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho tất cả các bài tập trong sách giáo khoa và sách bài tập.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả cao trong các kỳ thi.
Xét bài toán: Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức (F = x + 2y) với (left( {x;y} right)) là nghiệm của hệ bất phương trình (left{ begin{array}{l}x - 2y + 4 ge 0x + y - 5 le 0x ge 0y ge 0end{array} right.) (I) Miền nghiệm ({Omega }) của hệ (I) là miền tứ giác (OABC) (được tô màu) trên Hình 1. Với giá trị (F) cho trước, xét đường thẳng (d:x + 2y - F = 0) hay (y = - frac{x}{2} + frac{F}{2}). Trả lời các câu hỏi sau để giải bài toán tr
Trả lời câu hỏi Vận dụng trang 10 Chuyên đề học tập Toán 12 Chân trời sáng tạo
Cho bài toán quy hoạch tuyến tính
\(F = 3x + 3y \to \max ,\min \)
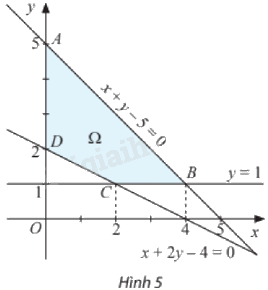
có tập phương án \({\Omega }\) là miền tứ giác \(ABCD\) (được tô màu như Hình 5) với các đỉnh là \(A\left( {0;5} \right),\)\(B\left( {4;1} \right),C\left( {2;1} \right)\) và \(D\left( {0;2} \right)\).
a) Giải bài toán quy hoạch tuyến tính đã cho.
b) Hàm mục tiêu \(F\) đạt giá trị lớn nhất trên \({\Omega }\) tại bao nhiêu điểm? Giải thích.
Phương pháp giải:
Bước 1: Biểu diễn tập phương án của bài toán trên mặt phẳng toạ độ \(Oxy\).
Bước 2: Tính giá trị của biểu thức \(F\) tại các đỉnh của \({\Omega }\).
Trong trường hợp tập phương án là miền đa giác thì giá trị lớn nhất (nhỏ nhất) trong các giá trị này là giá trị lớn nhất (nhỏ nhất) của \(F\) trên \({\Omega }\).
Trong trường hợp tập phương án không là miền đa giác nằm trong góc phần tư thứ nhất và các hệ số \(a\) và \(b\) không âm thì giá trị nhỏ nhất trong các giá trị này là giá trị nhỏ nhất của \(F\) trên \({\Omega }\).
Lời giải chi tiết:
a) Giá trị của biểu thức \(F\) tại các đỉnh của \({\Omega }\):
\(F\left( {0;5} \right) = 3.0 + 3\,.5 = 15;F\left( {4;1} \right) = 3\,.4 + 3\,.1 = 15;F\left( {2;1} \right) = 3.2 + 3\,.1 = 9;F\left( {0;2} \right) = 3\,.0 + 3\,.2 = 6\)
Do đó: \(\mathop {\max }\limits_{\Omega } F = F\left( {0;5} \right) = F\left( {4;1} \right) = 15;\mathop {\min }\limits_{\Omega } F = F\left( {0;2} \right) = 6\).
b) Tại mọi điểm \(\left( {x;y} \right)\) trên cạnh \(AB\) của miền \({\Omega }\), ta luôn có \(x + y - 5 = 0\) hay \(x + y = 5\).
Do đó \(F = 3x + 3y = 3\left( {x + y} \right) = 3.5 = 15\).
Vậy hàm mục tiêu \(F\) đạt giá trị lớn nhất trên \({\Omega }\) tại mọi điểm thuộc ạnh \(AB\) của miền \({\Omega }\).
Trả lời câu hỏi Hoạt động 2 trang 8 Chuyên đề học tập Toán 12 Chân trời sáng tạo
Xét bài toán quy hoạch tuyến tính:
\(F = 2x + y \to \max ,\min \)
với ràng buộc
\(\left\{ \begin{array}{l}x + y - 4 \ge 0\\3x - y \ge 0\\x \ge 0\\y \ge 1\end{array} \right.\) (II)
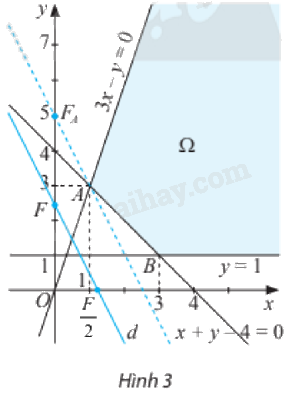
Tập phương án \({\Omega }\) của bài toán là phần được tô màu trên Hình 3. Hai điểm \(A\left( {1;3} \right)\) và \(B\left( {3;1} \right)\) gọi là các đỉnh của \({\Omega }\).
Với giá trị \(F\) cho trước, xét đường thẳng \(d:2x + y = F\) hay \(d:y = - 2x + F\).
Trả lời các câu hỏi sau để giải bài toán trên.
a) Tìm giá trị của \(F\) để đường thẳng \(d\) đi qua điểm \(A\left( {1;3} \right)\). Gọi giá trị tìm được là \({F_A}\).
b) Khi giá trị của \(F\) tăng (hoặc giảm) thì tung độ giao điểm của \(d\) với trục \(Oy\) thay đổi như thế nào? Khi đó, phương của đường thẳng \(d\) có thay đổi không?
c) Nếu \(F < {F_A}\) thì \(d\) và \({\Omega }\) có điểm chung không? Từ đó, chỉ ra giá trị nhỏ nhất của hàm mục tiêu \(F = 2x + y\) trên \({\Omega }\).
d) Với giá trị nào của \(F\) thì \(d\) và \({\Omega }\) có điểm chung? Hàm mục tiêu \(F = 2x + y\) giá trị lớn nhất trên \({\Omega }\) hay không?
Phương pháp giải:
‒ Đường thẳng \(d:ax + by + c = 0\) đi qua \(M\left( {{x_0};{y_0}} \right)\) khi \(a{x_0} + b{y_0} + c = 0\).
‒ Tìm tung độ giao điểm của \(d\) với trục \(Oy\) và nhận xét tính tăng giảm khi giá trị của \(F\) tăng (hoặc giảm).
Lời giải chi tiết:
a) Đường thẳng \(d\) đi qua điểm \(A\left( {1;3} \right)\) khi \(2.1 + 3 = F\) hay \(F = 5\).
Vậy \({F_A} = 5\).
b) Tung độ giao điểm của \(d\) với trục \(Oy\): \(y = - 2.0 + F = F\)
Do đó, khi giá trị của F tăng (hoặc giảm) thì tung độ giao điểm của \(d\) với trục \(Oy\) tăng (hoặc giảm) theo.
Đường thẳng \(d\) luôn có vectơ pháp tuyến \(\overrightarrow n = \left( {2;1} \right)\) nên phương của đường thẳng \(d\) không thay đổi.
c) Nếu \(F < {F_A}\) thì \(d\) và \({\Omega }\) không có điểm chung; Suy ra \(\mathop {\min }\limits_{\Omega }\) F = 5\).
d) \(d\) và \({\Omega }\) có điểm chung khi \(F \ge {F_A} = 5\).
Do đó hàm mục tiêu \(F = 2x + y\) không đạt giá trị lớn nhất trên \({\Omega }\).
Trả lời câu hỏi Hoạt động 1 trang 6 Chuyên đề học tập Toán 12 Chân trời sáng tạo
Xét bài toán: Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức \(F = x + 2y\) với \(\left( {x;y} \right)\) là nghiệm của hệ bất phương trình
\(\left\{ \begin{array}{l}x - 2y + 4 \ge 0\\x + y - 5 \le 0\\x \ge 0\\y \ge 0\end{array} \right.\) (I)
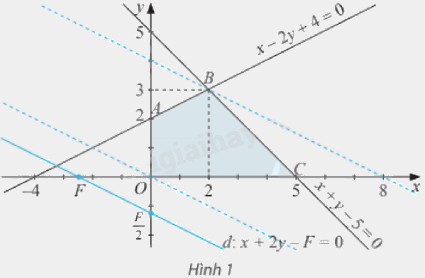
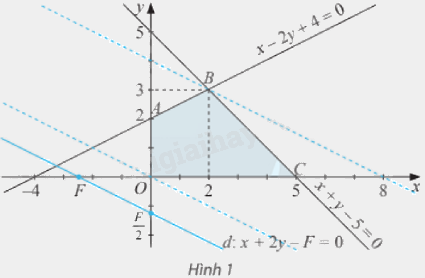
Miền nghiệm \({\Omega }\) của hệ (I) là miền tứ giác \(OABC\) (được tô màu) trên Hình 1. Với giá trị \(F\) cho trước, xét đường thẳng \(d:x + 2y - F = 0\) hay \(y = - \frac{x}{2} + \frac{F}{2}\).
Trả lời các câu hỏi sau để giải bài toán trên.
a) Với giá trị nào của \(F\) thì đường thẳng \(d\) đi qua điểm \(O\), điểm \(B\)?
b) Khi giá trị của \(F\) tăng (hoặc giảm) thì tung độ giao điểm của \(d\) với trục \(Oy\) thay đổi như thế nào? Khi đó, phương của đường thẳng \(d\) có thay đổi không?
c) Với điều kiện nào của \(F\) thì đường thẳng \(d\) và miền nghiệm \({\Omega }\) có điểm chung?
d) Từ đó, chỉ ra giá trị lớn nhất và giá trị nhỏ nhất của biểu thức \(F = x + 2y\) trên miền nghiệm \({\Omega }\). Biểu thức \(F\) đạt được các giá trị đó tại điểm nào?
Phương pháp giải:
‒ Đường thẳng \(d:ax + by + c = 0\) đi qua \(M\left( {{x_0};{y_0}} \right)\) khi \(a{x_0} + b{y_0} + c = 0\).
‒ Tìm tung độ giao điểm của \(d\) với trục \(Oy\) và nhận xét tính tăng giảm khi giá trị của \(F\) tăng (hoặc giảm).
‒ Giá trị lớn nhất và giá trị nhỏ nhất của biểu thức \(F = x + 2y\) trên miền nghiệm \({\Omega }\) đạt được tại các đỉnh của tứ giác.
Lời giải chi tiết:
a) Đường thẳng \(d\) đi qua điểm \(O\left( {0;0} \right)\) khi \(0 + 2.0 - F = 0\) hay \(F = 0\).
Đường thẳng \(d\) đi qua điểm \(B\left( {2;3} \right)\) khi \(2 + 2.3 - F = 0\) hay \(F = 8\).
b) Tung độ giao điểm của \(d\) với trục \(Oy\): \(y = - \frac{0}{2} + \frac{F}{2} = \frac{F}{2}\)
Do đó, khi giá trị của F tăng (hoặc giảm) thì tung độ giao điểm của \(d\) với trục \(Oy\) tăng (hoặc giảm) theo.
Đường thẳng \(d\) luôn có vectơ pháp tuyến \(\overrightarrow n = \left( {1;2} \right)\) nên phương của đường thẳng \(d\) không thay đổi.
c) Với điều kiện \(0 \le F \le 8\) thì đường thẳng \(d\) và miền nghiệm \({\Omega }\) có điểm chung.
d) Ta có: \(O\left( {0;0} \right),A\left( {0;2} \right),B\left( {2;3} \right),C\left( {5;0} \right)\).
Giá trị của biểu thức \(F\) tại các đỉnh của \({\Omega }\):
\(F\left( {0;0} \right) = 0,F\left( {0;2} \right) = 4,F\left( {2;3} \right) = 8,F\left( {5;0} \right) = 5\)
Do đó \(\mathop {\max }\limits_{\Omega } F = 8\) tại điểm \(B\left( {2;3} \right)\) và \(\mathop {\min }\limits_{\Omega } F = 0\) tại điểm \(O\left( {0;0} \right)\).
Trả lời câu hỏi Thực hành 1 trang 10 Chuyên đề học tập Toán 12 Chân trời sáng tạo
Giải bài toán quy hoạch tuyến tính:
\(F = 4x + 3y \to \max ,\min \)
với ràng buộc
\(\left\{ \begin{array}{l}x + 2y - 8 \le 0\\2x - y - 6 \le 0\\x \ge 0\\y \ge 1\end{array} \right.\)
Phương pháp giải:
Bước 1: Biểu diễn tập phương án của bài toán trên mặt phẳng toạ độ \(Oxy\).
Bước 2: Tính giá trị của biểu thức \(F\) tại các đỉnh của \({\Omega }\).
Trong trường hợp tập phương án là miền đa giác thì giá trị lớn nhất (nhỏ nhất) trong các giá trị này là giá trị lớn nhất (nhỏ nhất) của \(F\) trên \({\Omega }\).
Trong trường hợp tập phương án không là miền đa giác nằm trong góc phần tư thứ nhất và các hệ số \(a\) và \(b\) không âm thì giá trị nhỏ nhất trong các giá trị này là giá trị nhỏ nhất của \(F\) trên \({\Omega }\).
Lời giải chi tiết:
Tập phương án \({\Omega }\) là miền tứ giác \(ABCD\).
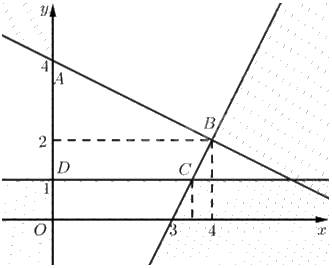
Toạ độ \(A\) là nghiệm của hệ \(\left\{ \begin{array}{l}x + 2y = 8\\x = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 0\\y = 4\end{array} \right.\). Vậy \(A\left( {0;4} \right)\)
Toạ độ \(B\) là nghiệm của hệ \(\left\{ \begin{array}{l}x + 2y = 8\\2{\rm{x}} - y = 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 4\\y = 2\end{array} \right.\). Vậy \(B\left( {4;2} \right)\)
Toạ độ \(C\) là nghiệm của hệ \(\left\{ \begin{array}{l}y = 1\\2{\rm{x}} - y = 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 3,5\\y = 1\end{array} \right.\). Vậy \(C\left( {3,5;1} \right)\)
Toạ độ \(D\) là nghiệm của hệ \(\left\{ \begin{array}{l}x = 0\\y = 1\end{array} \right.\). Vậy \(D\left( {0;1} \right)\)
Giá trị của biểu thức \(F\) tại các đỉnh của \({\Omega }\):
\(F\left( {0;4} \right) = 12;F\left( {4;2} \right) = 22;F\left( {3,5;1} \right) = 17;F\left( {0;1} \right) = 3\)
Do đó: \(\mathop {\max }\limits_{\Omega } F = F\left( {4;2} \right) = 22;\mathop {\min }\limits_{\Omega } F = F\left( {0;1} \right) = 3\).
Trả lời câu hỏi Thực hành 2 trang 10 Chuyên đề học tập Toán 12 Chân trời sáng tạo
Giải bài toán quy hoạch tuyến tính:
\(F = 25x + 10y \to \min \)
với ràng buộc
\(\left\{ \begin{array}{l}2{\rm{x}} - 3y \le 6\\x + y \ge 4\\x \ge 2\end{array} \right.\)
Phương pháp giải:
Bước 1: Biểu diễn tập phương án của bài toán trên mặt phẳng toạ độ \(Oxy\).
Bước 2: Tính giá trị của biểu thức \(F\) tại các đỉnh của \({\Omega }\).
Trong trường hợp tập phương án là miền đa giác thì giá trị lớn nhất (nhỏ nhất) trong các giá trị này là giá trị lớn nhất (nhỏ nhất) của \(F\) trên \({\Omega }\).
Trong trường hợp tập phương án không là miền đa giác nằm trong góc phần tư thứ nhất và các hệ số \(a\) và \(b\) không âm thì giá trị nhỏ nhất trong các giá trị này là giá trị nhỏ nhất của \(F\) trên \({\Omega }\).
Lời giải chi tiết:
Viết lại ràng buộc của bài toán thành
\(\left\{ \begin{array}{l}2{\rm{x}} - 3y - 6 \le 0\\x + y - 4 \ge 0\\x \ge 2\end{array} \right.\)
Tập phương án \({\Omega }\) của bài toán là miền không gạch (không là miền đa giác).
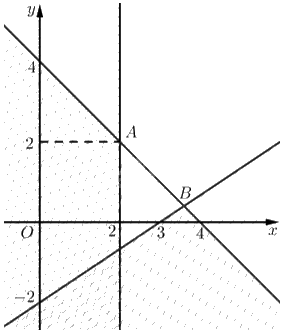
Toạ độ \(A\) là nghiệm của hệ \(\left\{ \begin{array}{l}x = 2\\x + y = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 2\end{array} \right.\). Vậy \(A\left( {2;2} \right)\).
Toạ độ \(B\) là nghiệm của hệ \(\left\{ \begin{array}{l}2x - 3y = 6\\x + y = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \frac{{18}}{5}\\y = \frac{2}{5}\end{array} \right.\). Vậy \(B\left( {\frac{{18}}{5};\frac{2}{5}} \right)\).
Do \({\Omega }\) nằm trong góc phần tư thứ nhất và các hệ số của biểu thức \(F = 25x + 10y\) đều dương nên \(F\) đạt giá trị nhỏ nhất tại một đỉnh của \({\Omega }\).
Ta có \(F\left( {2;2} \right) = 25\,.\,2 + 10\,.\,2 = 70;F\left( {\frac{{18}}{5};\frac{2}{5}} \right) = 25 \cdot \frac{{18}}{5} + 10 \cdot \frac{2}{5} = 94\).
Do đó \(F\) đạt giá trị nhỏ nhất tại đỉnh \(A\left( {2;2} \right)\) và \(\mathop {\min }\limits_{\Omega } F = F\left( {2;2} \right) = 70\).
Trả lời câu hỏi Hoạt động 1 trang 6 Chuyên đề học tập Toán 12 Chân trời sáng tạo
Xét bài toán: Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức \(F = x + 2y\) với \(\left( {x;y} \right)\) là nghiệm của hệ bất phương trình
\(\left\{ \begin{array}{l}x - 2y + 4 \ge 0\\x + y - 5 \le 0\\x \ge 0\\y \ge 0\end{array} \right.\) (I)
Miền nghiệm \({\Omega }\) của hệ (I) là miền tứ giác \(OABC\) (được tô màu) trên Hình 1. Với giá trị \(F\) cho trước, xét đường thẳng \(d:x + 2y - F = 0\) hay \(y = - \frac{x}{2} + \frac{F}{2}\).
Trả lời các câu hỏi sau để giải bài toán trên.
a) Với giá trị nào của \(F\) thì đường thẳng \(d\) đi qua điểm \(O\), điểm \(B\)?
b) Khi giá trị của \(F\) tăng (hoặc giảm) thì tung độ giao điểm của \(d\) với trục \(Oy\) thay đổi như thế nào? Khi đó, phương của đường thẳng \(d\) có thay đổi không?
c) Với điều kiện nào của \(F\) thì đường thẳng \(d\) và miền nghiệm \({\Omega }\) có điểm chung?
d) Từ đó, chỉ ra giá trị lớn nhất và giá trị nhỏ nhất của biểu thức \(F = x + 2y\) trên miền nghiệm \({\Omega }\). Biểu thức \(F\) đạt được các giá trị đó tại điểm nào?
Phương pháp giải:
‒ Đường thẳng \(d:ax + by + c = 0\) đi qua \(M\left( {{x_0};{y_0}} \right)\) khi \(a{x_0} + b{y_0} + c = 0\).
‒ Tìm tung độ giao điểm của \(d\) với trục \(Oy\) và nhận xét tính tăng giảm khi giá trị của \(F\) tăng (hoặc giảm).
‒ Giá trị lớn nhất và giá trị nhỏ nhất của biểu thức \(F = x + 2y\) trên miền nghiệm \({\Omega }\) đạt được tại các đỉnh của tứ giác.
Lời giải chi tiết:
a) Đường thẳng \(d\) đi qua điểm \(O\left( {0;0} \right)\) khi \(0 + 2.0 - F = 0\) hay \(F = 0\).
Đường thẳng \(d\) đi qua điểm \(B\left( {2;3} \right)\) khi \(2 + 2.3 - F = 0\) hay \(F = 8\).
b) Tung độ giao điểm của \(d\) với trục \(Oy\): \(y = - \frac{0}{2} + \frac{F}{2} = \frac{F}{2}\)
Do đó, khi giá trị của F tăng (hoặc giảm) thì tung độ giao điểm của \(d\) với trục \(Oy\) tăng (hoặc giảm) theo.
Đường thẳng \(d\) luôn có vectơ pháp tuyến \(\overrightarrow n = \left( {1;2} \right)\) nên phương của đường thẳng \(d\) không thay đổi.
c) Với điều kiện \(0 \le F \le 8\) thì đường thẳng \(d\) và miền nghiệm \({\Omega }\) có điểm chung.
d) Ta có: \(O\left( {0;0} \right),A\left( {0;2} \right),B\left( {2;3} \right),C\left( {5;0} \right)\).
Giá trị của biểu thức \(F\) tại các đỉnh của \({\Omega }\):
\(F\left( {0;0} \right) = 0,F\left( {0;2} \right) = 4,F\left( {2;3} \right) = 8,F\left( {5;0} \right) = 5\)
Do đó \(\mathop {\max }\limits_{\Omega } F = 8\) tại điểm \(B\left( {2;3} \right)\) và \(\mathop {\min }\limits_{\Omega } F = 0\) tại điểm \(O\left( {0;0} \right)\).
Trả lời câu hỏi Hoạt động 2 trang 8 Chuyên đề học tập Toán 12 Chân trời sáng tạo
Xét bài toán quy hoạch tuyến tính:
\(F = 2x + y \to \max ,\min \)
với ràng buộc
\(\left\{ \begin{array}{l}x + y - 4 \ge 0\\3x - y \ge 0\\x \ge 0\\y \ge 1\end{array} \right.\) (II)
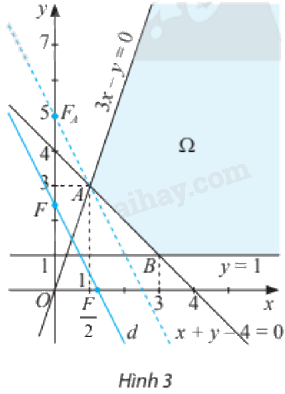
Tập phương án \({\Omega }\) của bài toán là phần được tô màu trên Hình 3. Hai điểm \(A\left( {1;3} \right)\) và \(B\left( {3;1} \right)\) gọi là các đỉnh của \({\Omega }\).
Với giá trị \(F\) cho trước, xét đường thẳng \(d:2x + y = F\) hay \(d:y = - 2x + F\).
Trả lời các câu hỏi sau để giải bài toán trên.
a) Tìm giá trị của \(F\) để đường thẳng \(d\) đi qua điểm \(A\left( {1;3} \right)\). Gọi giá trị tìm được là \({F_A}\).
b) Khi giá trị của \(F\) tăng (hoặc giảm) thì tung độ giao điểm của \(d\) với trục \(Oy\) thay đổi như thế nào? Khi đó, phương của đường thẳng \(d\) có thay đổi không?
c) Nếu \(F < {F_A}\) thì \(d\) và \({\Omega }\) có điểm chung không? Từ đó, chỉ ra giá trị nhỏ nhất của hàm mục tiêu \(F = 2x + y\) trên \({\Omega }\).
d) Với giá trị nào của \(F\) thì \(d\) và \({\Omega }\) có điểm chung? Hàm mục tiêu \(F = 2x + y\) giá trị lớn nhất trên \({\Omega }\) hay không?
Phương pháp giải:
‒ Đường thẳng \(d:ax + by + c = 0\) đi qua \(M\left( {{x_0};{y_0}} \right)\) khi \(a{x_0} + b{y_0} + c = 0\).
‒ Tìm tung độ giao điểm của \(d\) với trục \(Oy\) và nhận xét tính tăng giảm khi giá trị của \(F\) tăng (hoặc giảm).
Lời giải chi tiết:
a) Đường thẳng \(d\) đi qua điểm \(A\left( {1;3} \right)\) khi \(2.1 + 3 = F\) hay \(F = 5\).
Vậy \({F_A} = 5\).
b) Tung độ giao điểm của \(d\) với trục \(Oy\): \(y = - 2.0 + F = F\)
Do đó, khi giá trị của F tăng (hoặc giảm) thì tung độ giao điểm của \(d\) với trục \(Oy\) tăng (hoặc giảm) theo.
Đường thẳng \(d\) luôn có vectơ pháp tuyến \(\overrightarrow n = \left( {2;1} \right)\) nên phương của đường thẳng \(d\) không thay đổi.
c) Nếu \(F < {F_A}\) thì \(d\) và \({\Omega }\) không có điểm chung; Suy ra \(\mathop {\min }\limits_{\Omega }\) F = 5\).
d) \(d\) và \({\Omega }\) có điểm chung khi \(F \ge {F_A} = 5\).
Do đó hàm mục tiêu \(F = 2x + y\) không đạt giá trị lớn nhất trên \({\Omega }\).
Trả lời câu hỏi Thực hành 1 trang 10 Chuyên đề học tập Toán 12 Chân trời sáng tạo
Giải bài toán quy hoạch tuyến tính:
\(F = 4x + 3y \to \max ,\min \)
với ràng buộc
\(\left\{ \begin{array}{l}x + 2y - 8 \le 0\\2x - y - 6 \le 0\\x \ge 0\\y \ge 1\end{array} \right.\)
Phương pháp giải:
Bước 1: Biểu diễn tập phương án của bài toán trên mặt phẳng toạ độ \(Oxy\).
Bước 2: Tính giá trị của biểu thức \(F\) tại các đỉnh của \({\Omega }\).
Trong trường hợp tập phương án là miền đa giác thì giá trị lớn nhất (nhỏ nhất) trong các giá trị này là giá trị lớn nhất (nhỏ nhất) của \(F\) trên \({\Omega }\).
Trong trường hợp tập phương án không là miền đa giác nằm trong góc phần tư thứ nhất và các hệ số \(a\) và \(b\) không âm thì giá trị nhỏ nhất trong các giá trị này là giá trị nhỏ nhất của \(F\) trên \({\Omega }\).
Lời giải chi tiết:
Tập phương án \({\Omega }\) là miền tứ giác \(ABCD\).
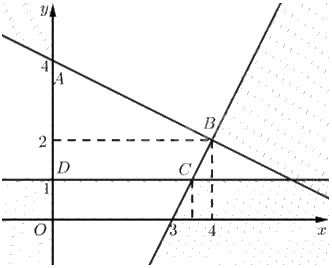
Toạ độ \(A\) là nghiệm của hệ \(\left\{ \begin{array}{l}x + 2y = 8\\x = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 0\\y = 4\end{array} \right.\). Vậy \(A\left( {0;4} \right)\)
Toạ độ \(B\) là nghiệm của hệ \(\left\{ \begin{array}{l}x + 2y = 8\\2{\rm{x}} - y = 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 4\\y = 2\end{array} \right.\). Vậy \(B\left( {4;2} \right)\)
Toạ độ \(C\) là nghiệm của hệ \(\left\{ \begin{array}{l}y = 1\\2{\rm{x}} - y = 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 3,5\\y = 1\end{array} \right.\). Vậy \(C\left( {3,5;1} \right)\)
Toạ độ \(D\) là nghiệm của hệ \(\left\{ \begin{array}{l}x = 0\\y = 1\end{array} \right.\). Vậy \(D\left( {0;1} \right)\)
Giá trị của biểu thức \(F\) tại các đỉnh của \({\Omega }\):
\(F\left( {0;4} \right) = 12;F\left( {4;2} \right) = 22;F\left( {3,5;1} \right) = 17;F\left( {0;1} \right) = 3\)
Do đó: \(\mathop {\max }\limits_{\Omega } F = F\left( {4;2} \right) = 22;\mathop {\min }\limits_{\Omega } F = F\left( {0;1} \right) = 3\).
Trả lời câu hỏi Thực hành 2 trang 10 Chuyên đề học tập Toán 12 Chân trời sáng tạo
Giải bài toán quy hoạch tuyến tính:
\(F = 25x + 10y \to \min \)
với ràng buộc
\(\left\{ \begin{array}{l}2{\rm{x}} - 3y \le 6\\x + y \ge 4\\x \ge 2\end{array} \right.\)
Phương pháp giải:
Bước 1: Biểu diễn tập phương án của bài toán trên mặt phẳng toạ độ \(Oxy\).
Bước 2: Tính giá trị của biểu thức \(F\) tại các đỉnh của \({\Omega }\).
Trong trường hợp tập phương án là miền đa giác thì giá trị lớn nhất (nhỏ nhất) trong các giá trị này là giá trị lớn nhất (nhỏ nhất) của \(F\) trên \({\Omega }\).
Trong trường hợp tập phương án không là miền đa giác nằm trong góc phần tư thứ nhất và các hệ số \(a\) và \(b\) không âm thì giá trị nhỏ nhất trong các giá trị này là giá trị nhỏ nhất của \(F\) trên \({\Omega }\).
Lời giải chi tiết:
Viết lại ràng buộc của bài toán thành
\(\left\{ \begin{array}{l}2{\rm{x}} - 3y - 6 \le 0\\x + y - 4 \ge 0\\x \ge 2\end{array} \right.\)
Tập phương án \({\Omega }\) của bài toán là miền không gạch (không là miền đa giác).
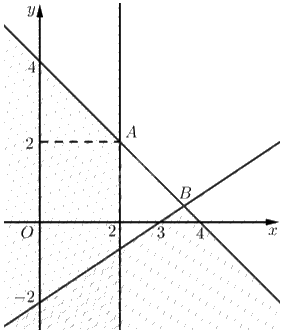
Toạ độ \(A\) là nghiệm của hệ \(\left\{ \begin{array}{l}x = 2\\x + y = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 2\end{array} \right.\). Vậy \(A\left( {2;2} \right)\).
Toạ độ \(B\) là nghiệm của hệ \(\left\{ \begin{array}{l}2x - 3y = 6\\x + y = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \frac{{18}}{5}\\y = \frac{2}{5}\end{array} \right.\). Vậy \(B\left( {\frac{{18}}{5};\frac{2}{5}} \right)\).
Do \({\Omega }\) nằm trong góc phần tư thứ nhất và các hệ số của biểu thức \(F = 25x + 10y\) đều dương nên \(F\) đạt giá trị nhỏ nhất tại một đỉnh của \({\Omega }\).
Ta có \(F\left( {2;2} \right) = 25\,.\,2 + 10\,.\,2 = 70;F\left( {\frac{{18}}{5};\frac{2}{5}} \right) = 25 \cdot \frac{{18}}{5} + 10 \cdot \frac{2}{5} = 94\).
Do đó \(F\) đạt giá trị nhỏ nhất tại đỉnh \(A\left( {2;2} \right)\) và \(\mathop {\min }\limits_{\Omega } F = F\left( {2;2} \right) = 70\).
Trả lời câu hỏi Vận dụng trang 10 Chuyên đề học tập Toán 12 Chân trời sáng tạo
Cho bài toán quy hoạch tuyến tính
\(F = 3x + 3y \to \max ,\min \)
có tập phương án \({\Omega }\) là miền tứ giác \(ABCD\) (được tô màu như Hình 5) với các đỉnh là \(A\left( {0;5} \right),\)\(B\left( {4;1} \right),C\left( {2;1} \right)\) và \(D\left( {0;2} \right)\).
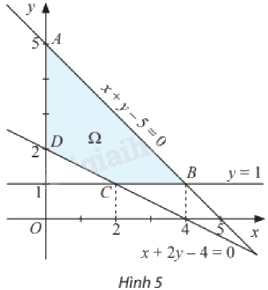
a) Giải bài toán quy hoạch tuyến tính đã cho.
b) Hàm mục tiêu \(F\) đạt giá trị lớn nhất trên \({\Omega }\) tại bao nhiêu điểm? Giải thích.
Phương pháp giải:
Bước 1: Biểu diễn tập phương án của bài toán trên mặt phẳng toạ độ \(Oxy\).
Bước 2: Tính giá trị của biểu thức \(F\) tại các đỉnh của \({\Omega }\).
Trong trường hợp tập phương án là miền đa giác thì giá trị lớn nhất (nhỏ nhất) trong các giá trị này là giá trị lớn nhất (nhỏ nhất) của \(F\) trên \({\Omega }\).
Trong trường hợp tập phương án không là miền đa giác nằm trong góc phần tư thứ nhất và các hệ số \(a\) và \(b\) không âm thì giá trị nhỏ nhất trong các giá trị này là giá trị nhỏ nhất của \(F\) trên \({\Omega }\).
Lời giải chi tiết:
a) Giá trị của biểu thức \(F\) tại các đỉnh của \({\Omega }\):
\(F\left( {0;5} \right) = 3.0 + 3\,.5 = 15;F\left( {4;1} \right) = 3\,.4 + 3\,.1 = 15;F\left( {2;1} \right) = 3.2 + 3\,.1 = 9;F\left( {0;2} \right) = 3\,.0 + 3\,.2 = 6\)
Do đó: \(\mathop {\max }\limits_{\Omega } F = F\left( {0;5} \right) = F\left( {4;1} \right) = 15;\mathop {\min }\limits_{\Omega } F = F\left( {0;2} \right) = 6\).
b) Tại mọi điểm \(\left( {x;y} \right)\) trên cạnh \(AB\) của miền \({\Omega }\), ta luôn có \(x + y - 5 = 0\) hay \(x + y = 5\).
Do đó \(F = 3x + 3y = 3\left( {x + y} \right) = 3.5 = 15\).
Vậy hàm mục tiêu \(F\) đạt giá trị lớn nhất trên \({\Omega }\) tại mọi điểm thuộc ạnh \(AB\) của miền \({\Omega }\).
Mục 1 của Chuyên đề học tập Toán 12 - Chân trời sáng tạo thường tập trung vào một chủ đề quan trọng, đặt nền móng cho các kiến thức tiếp theo. Việc nắm vững nội dung và phương pháp giải các bài tập trong mục này là vô cùng cần thiết. Bài viết này sẽ cung cấp lời giải chi tiết cho từng bài tập trang 6, 7, 8, 9, 10, giúp các em hiểu rõ bản chất vấn đề và tự tin giải quyết các bài toán tương tự.
Giải bài tập 1: (Nêu lại đề bài). Lời giải: (Giải chi tiết từng bước, kèm theo giải thích rõ ràng). Lưu ý: (Ghi chú những điểm quan trọng cần nhớ khi giải bài tập này).
Giải bài tập 2: (Nêu lại đề bài). Lời giải: (Giải chi tiết từng bước, kèm theo giải thích rõ ràng). Lưu ý: (Ghi chú những điểm quan trọng cần nhớ khi giải bài tập này).
Giải bài tập 3: (Nêu lại đề bài). Lời giải: (Giải chi tiết từng bước, kèm theo giải thích rõ ràng). Lưu ý: (Ghi chú những điểm quan trọng cần nhớ khi giải bài tập này).
Giải bài tập 4: (Nêu lại đề bài). Lời giải: (Giải chi tiết từng bước, kèm theo giải thích rõ ràng). Lưu ý: (Ghi chú những điểm quan trọng cần nhớ khi giải bài tập này).
Giải bài tập 5: (Nêu lại đề bài). Lời giải: (Giải chi tiết từng bước, kèm theo giải thích rõ ràng). Lưu ý: (Ghi chú những điểm quan trọng cần nhớ khi giải bài tập này).
Giải bài tập 6: (Nêu lại đề bài). Lời giải: (Giải chi tiết từng bước, kèm theo giải thích rõ ràng). Lưu ý: (Ghi chú những điểm quan trọng cần nhớ khi giải bài tập này).
Giải bài tập 7: (Nêu lại đề bài). Lời giải: (Giải chi tiết từng bước, kèm theo giải thích rõ ràng). Lưu ý: (Ghi chú những điểm quan trọng cần nhớ khi giải bài tập này).
Giải bài tập 8: (Nêu lại đề bài). Lời giải: (Giải chi tiết từng bước, kèm theo giải thích rõ ràng). Lưu ý: (Ghi chú những điểm quan trọng cần nhớ khi giải bài tập này).
Giải bài tập 9: (Nêu lại đề bài). Lời giải: (Giải chi tiết từng bước, kèm theo giải thích rõ ràng). Lưu ý: (Ghi chú những điểm quan trọng cần nhớ khi giải bài tập này).
Giải bài tập 10: (Nêu lại đề bài). Lời giải: (Giải chi tiết từng bước, kèm theo giải thích rõ ràng). Lưu ý: (Ghi chú những điểm quan trọng cần nhớ khi giải bài tập này).
Giải bài tập 11: (Nêu lại đề bài). Lời giải: (Giải chi tiết từng bước, kèm theo giải thích rõ ràng). Lưu ý: (Ghi chú những điểm quan trọng cần nhớ khi giải bài tập này).
Giải bài tập 12: (Nêu lại đề bài). Lời giải: (Giải chi tiết từng bước, kèm theo giải thích rõ ràng). Lưu ý: (Ghi chú những điểm quan trọng cần nhớ khi giải bài tập này).
Giải bài tập 13: (Nêu lại đề bài). Lời giải: (Giải chi tiết từng bước, kèm theo giải thích rõ ràng). Lưu ý: (Ghi chú những điểm quan trọng cần nhớ khi giải bài tập này).
Giải bài tập 14: (Nêu lại đề bài). Lời giải: (Giải chi tiết từng bước, kèm theo giải thích rõ ràng). Lưu ý: (Ghi chú những điểm quan trọng cần nhớ khi giải bài tập này).
Giải bài tập 15: (Nêu lại đề bài). Lời giải: (Giải chi tiết từng bước, kèm theo giải thích rõ ràng). Lưu ý: (Ghi chú những điểm quan trọng cần nhớ khi giải bài tập này).
Để giải các bài tập Toán 12 Chân trời sáng tạo một cách hiệu quả, các em cần:
Đừng ngần ngại hỏi thầy cô hoặc bạn bè nếu gặp khó khăn trong quá trình giải bài tập. Hãy chủ động tìm kiếm các nguồn tài liệu tham khảo khác để mở rộng kiến thức. Chúc các em học tập tốt và đạt kết quả cao!