Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 12 Chân trời sáng tạo tại giaitoan.edu.vn. Chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho mục 2 trang 11, 12, 13, giúp các em nắm vững kiến thức và tự tin giải các bài tập tương tự.
Với đội ngũ giáo viên giàu kinh nghiệm, chúng tôi cam kết mang đến cho các em những giải pháp học tập hiệu quả nhất.
Xét tình huống thương nhân thu mua trái cây ở Bài toán mở đầu (trang 6). a) Nếu gọi (x,y) (tính theo tấn) lần lượt là khối lượng trái cây loại A và B được thương nhân thu mua thì (x) và (y) phải thoả mãn hệ bất phương trình bậc nhất hai ẩn nào? b) Từ đó, phát biểu bài toán quy hoạch tuyến tính tìm khối lượng thu mua mỗi loại trái cây để thu được lợi nhuận cao nhất. Giải bài toán đó.
Trả lời câu hỏi Thực hành 4 trang 13 Chuyên đề học tập Toán 12 Chân trời sáng tạo
Trong 100 g thịt bò loại I có chứa 21 g protein và 3,5 g lipid; 100 g thịt bò loại II có chứa 18 g protein và 10,5 g lipid. Biết rằng thịt bò loại I có giá 220 nghìn đồng/kg thì thịt bò loại II có giá 210 nghìn đồng/kg. Để có lượng thực phẩm từ hai loại thịt bò trên cung cấp ít nhất 630 g protein và 210 g lipid, cần mua khối lượng bao nhiêu cho mỗi loại thịt bò loại I và II sao cho chi phí thấp nhất?
Phương pháp giải:
Bước 1: Đặt hai ẩn biểu thị hai đại lượng chưa biết (cần tìm). Viết điều kiện có nghĩa cho các ẩn đó.
Bước 2: Từ dữ kiện của bài toán, viết biểu thức biểu thị đại lượng cần tìm giá trị tối ưu và các bất phương trình bậc nhất đối với hai ẩn trên. Từ đó phát biểu bài toán quy hoạch tuyến tính nhận được.
Bước 3: Giải bài toán quy hoạch tuyến tính và trả lời.
Lời giải chi tiết:
Gọi \(x,y\) (\(x \ge 0,y \ge 0\), tính theo 100g) lần lượt là khối lượng của thịt bò loại I và loại II cần dùng.
Do cần cung cấp ít nhất 630g protein nên ta có \(21x + 18y \ge 630\) hay \(7x + 6y - 210 \ge 0\).
Do cần cung cấp ít nhất 210g lipid nên ta có \(3,5x + 10,5y \ge 210\) hay \(x + 3y - 60 \ge 0\).
Ta có: 220 nghìn đồng/kg=22 nghìn đồng/100g; 210 nghìn đồng/kg=21 nghìn đồng/100g.
Chi phí để mua thịt bò là \(F = 22x + 21y\) (nghìn đồng).
Từ đó, ta cần giải bài toán quy hoạch tuyến tính: \(F = 22x + 21y \to \min \) với ràng buộc \(\left\{ \begin{array}{l}7{\rm{x}} + 6y - 210 \ge 0\\x + 3y - 60 \ge 0\\x \ge 0\\y \ge 0\end{array} \right.\)
Tập phương án \({\Omega }\) của bài toán là miền không gạch (không là miền đa giác).
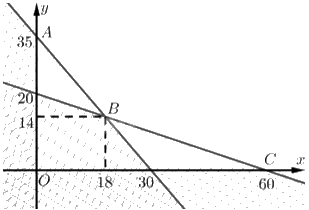
Toạ độ \(A\) là nghiệm của hệ \(\left\{ \begin{array}{l}7{\rm{x}} + 6y = 210\\x = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 0\\y = 35\end{array} \right.\). Vậy \(A\left( {0;35} \right)\).
Toạ độ \(B\) là nghiệm của hệ \(\left\{ \begin{array}{l}7{\rm{x}} + 6y = 210\\x + 3y = 60\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 18\\y = 14\end{array} \right.\). Vậy \(B\left( {18;14} \right)\).
Toạ độ \(C\) là nghiệm của hệ \(\left\{ \begin{array}{l}x + 3y = 60\\y = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 60\\y = 0\end{array} \right.\). Vậy \(C\left( {60;0} \right)\).
Giá trị của biểu thức \(F\) tại các đỉnh của \({\Omega }\):
\(F\left( {0;35} \right) = 22.0 + 21.35 = 735;F\left( {18;14} \right) = 22.18 + 21.14 = 690;F\left( {60;0} \right) = 22.60 + 21.0 = 1320\)
Do đó: \(\mathop {\min }\limits_{\Omega } F = F\left( {18;14} \right) = 690\).
Vậy cần mua \(18.100g = 1,8kg\) thịt bò loại I và \(14.100g = 1,4kg\) thịt bò loại II.
Trả lời câu hỏi Hoạt động 3 trang 11 Chuyên đề học tập Toán 12 Chân trời sáng tạo
Xét tình huống thương nhân thu mua trái cây ở Bài toán mở đầu (trang 6).
a) Nếu gọi \(x,y\) (tính theo tấn) lần lượt là khối lượng trái cây loại A và B được thương nhân thu mua thì \(x\) và \(y\) phải thoả mãn hệ bất phương trình bậc nhất hai ẩn nào?
b) Từ đó, phát biểu bài toán quy hoạch tuyến tính tìm khối lượng thu mua mỗi loại trái cây để thu được lợi nhuận cao nhất. Giải bài toán đó.
Phương pháp giải:
‒ Biểu diễn các đại lượng chưa biết thông qua các đại lượng đã biết và ẩn để lập bài toán quy hoạch tuyến tính.
‒ Giải bài toán quy hoạch tuyến tính:
Bước 1: Biểu diễn tập phương án của bài toán trên mặt phẳng toạ độ \(Oxy\).
Bước 2: Tính giá trị của biểu thức \(F\) tại các đỉnh của \({\Omega }\).
Trong trường hợp tập phương án là miền đa giác thì giá trị lớn nhất (nhỏ nhất) trong các giá trị này là giá trị lớn nhất (nhỏ nhất) của \(F\) trên \({\Omega }\).
Trong trường hợp tập phương án không là miền đa giác nằm trong góc phần tư thứ nhất và các hệ số \(a\) và \(b\) không âm thì giá trị nhỏ nhất trong các giá trị này là giá trị nhỏ nhất của \(F\) trên \({\Omega }\).
Lời giải chi tiết:
a) Gọi \(x,y\) tấn \(\left( {x \ge 0,y \ge 0} \right)\) lần lượt là khối lượng trái cây loại A và B được thương nhân thu mua.
Thương nhân đó mua tối đa 8 tấn trái cây nên ta có phương trình sau: \(x + y \le 8\).
Số tiền mua loại trái cây A là \(12{\rm{x}}\) triệu đồng.
Số tiền mua loại trái cây B là \(20{\rm{y}}\) triệu đồng.
Tổng số tiền mua trái cây không vượt quá 120 triệu đồng nên ta có phương trình sau: \(12{\rm{x}} + 20y \le 120\) hay \(3{\rm{x}} + 5y \le 30\).
Do đó ta có hệ bất phương trình sau: \(\left\{ \begin{array}{l}x + y \le 8\\3x + 5y \le 30\\x \ge 0\\y \ge 0\end{array} \right.\).
Lợi nhuận khi bán trái cây loại A là \(1,1{\rm{x}}\) triệu đồng.
Lợi nhuận khi bán trái cây loại B là \(1,5y\) triệu đồng.
Lợi nhuận thương nhân đó thu được là: \(F = 1,1{\rm{x}} + 1,5y\) triệu đồng.
b) Ta cần giải bài toán quy hoạch tuyến tính: \(F = 1,1x + 1,5y \to \max \), với ràng buộc \(\left\{ \begin{array}{l}x + y \le 8\\3x + 5y \le 30\\x \ge 0\\y \ge 0\end{array} \right.\)
Tập phương án \({\Omega }\) là miền tứ giác \(ABCD\).
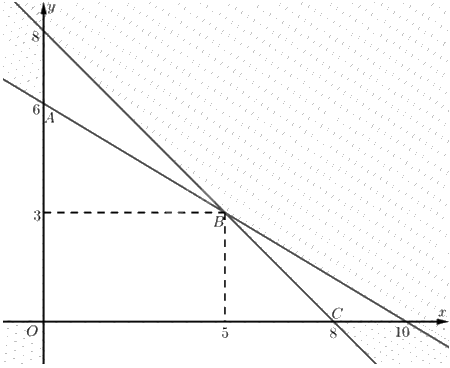
Toạ độ \(A\) là nghiệm của hệ \(\left\{ \begin{array}{l}3{\rm{x}} + 5y = 30\\x = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 0\\y = 6\end{array} \right.\). Vậy \(A\left( {0;6} \right)\).
Toạ độ \(B\) là nghiệm của hệ \(\left\{ \begin{array}{l}3{\rm{x}} + 5y = 30\\x + y = 8\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 5\\y = 3\end{array} \right.\). Vậy \(B\left( {5;3} \right)\).
Toạ độ \(C\) là nghiệm của hệ \(\left\{ \begin{array}{l}x + y = 8\\y = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 8\\y = 0\end{array} \right.\). Vậy \(C\left( {8;0} \right)\)
Giá trị của biểu thức \(F\) tại các đỉnh của \({\Omega }\):
\(\begin{array}{l}F\left( {0;0} \right) = 1,1\,.0 + 1,5\,.0 = 0;F\left( {0;6} \right) = 1,1\,.0 + 1,5\,.6 = 9;\\F\left( {5;3} \right) = 1,1\,.5 + 1,5\,.3 = 10;F\left( {8;0} \right) = 1,1\,.8 + 1,5\,.0 = 8,8\end{array}\)
Do đó: \(\mathop {\max }\limits_{\Omega } F = F\left( {5;3} \right) = 10\).
Vậy thương nhân cần mua 5 tấn loại A và 3 tấn loại B thì thu được lợi nhuận cao nhất.
Trả lời câu hỏi Thực hành 3 trang 13 Chuyên đề học tập Toán 12 Chân trời sáng tạo
Một dây chuyền của nhà máy sản xuất đá xây dựng dự định sản xuất hai loại sản phẩm A và B. Thời gian để dây chuyền sản xuất 100 tấn sản phẩm loại A và 100 tấn sản phẩm loại B lần lượt là 2 giờ và 3 giờ. Do nhu cầu thị trường, xí nghiệp sản xuất sản lượng sản phẩm loại A không ít hơn 3 lần sản lượng sản phẩm loại B. Sản phẩm loại A cho lợi nhuận là 5 triệu đồng/100 tấn; sản phẩm loại B cho lợi nhuận 9 triệu đồng/100 tấn.
Trong thời gian không quá 6 giờ làm việc của dây chuyền, cần sản xuất bao nhiêu tấn sản phẩm loại A, bao nhiêu tấn sản phẩm loại B để thu được lợi nhuận cao nhất?

Phương pháp giải:
Bước 1: Đặt hai ẩn biểu thị hai đại lượng chưa biết (cần tìm). Viết điều kiện có nghĩa cho các ẩn đó.
Bước 2: Từ dữ kiện của bài toán, viết biểu thức biểu thị đại lượng cần tìm giá trị tối ưu và các bất phương trình bậc nhất đối với hai ẩn trên. Từ đó phát biểu bài toán quy hoạch tuyến tính nhận được.
Bước 3: Giải bài toán quy hoạch tuyến tính và trả lời.
Lời giải chi tiết:
Gọi \(x,y\) tấn \(\left( {x \ge 0,y \ge 0} \right)\) lần lượt là sản lượng sản phẩm loại A và loại B xí nghiệp đó sản xuất.
Do thời gian làm việc của dây chuyền không quá 6 giờ nên \(2x + 3y \le 6\) hay \(2x + 3y - 6 \le 0\).
Do sản lượng sản phẩm loại A không ít hơn 3 lần sản lượng sản phẩm B nên \(x \ge 3y\) hay \(x - 3y \ge 0\).
Lợi nhuận thu được là \(F = 5x + 9y\) (triệu đồng).
Từ đó, ta cần giải bài toán quy hoạch tuyến tính: \(F = 5x + 9y \to \max \) với ràng buộc \(\left\{ \begin{array}{l}2x + 3y - 6 \le 0\\x - 3y \ge 0\\x \ge 0\\y \ge 0\end{array} \right.\)
Tập phương án \({\Omega }\) là miền tam giác \(OAB\).
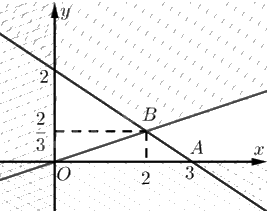
Toạ độ \(A\) là nghiệm của hệ \(\left\{ \begin{array}{l}2{\rm{x}} + 3y = 6\\y = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 3\\y = 0\end{array} \right.\). Vậy \(A\left( {3;0} \right)\).
Toạ độ \(B\) là nghiệm của hệ \(\left\{ \begin{array}{l}2{\rm{x}} + 3y = 6\\x - 3y = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = \frac{2}{3}\end{array} \right.\). Vậy \(B\left( {2;\frac{2}{3}} \right)\).
Giá trị của biểu thức \(F\) tại các đỉnh của \({\Omega }\):
\(F\left( {0;0} \right) = 5.0 + 9.0 = 0;F\left( {3;0} \right) = 5.3 + 9.0 = 15;F\left( {2;\frac{2}{3}} \right) = 5.2 + 9.\frac{2}{3} = 16\)
Do đó: \(\mathop {\max }\limits_{\Omega } F = F\left( {2;\frac{2}{3}} \right) = 16\).
Vậy xí nghiệp cần sản xuất 200 tấn loại A và \(\frac{{200}}{3}\) tấn loại B thì thu được lợi nhuận cao nhất.
Trả lời câu hỏi Hoạt động 3 trang 11 Chuyên đề học tập Toán 12 Chân trời sáng tạo
Xét tình huống thương nhân thu mua trái cây ở Bài toán mở đầu (trang 6).
a) Nếu gọi \(x,y\) (tính theo tấn) lần lượt là khối lượng trái cây loại A và B được thương nhân thu mua thì \(x\) và \(y\) phải thoả mãn hệ bất phương trình bậc nhất hai ẩn nào?
b) Từ đó, phát biểu bài toán quy hoạch tuyến tính tìm khối lượng thu mua mỗi loại trái cây để thu được lợi nhuận cao nhất. Giải bài toán đó.
Phương pháp giải:
‒ Biểu diễn các đại lượng chưa biết thông qua các đại lượng đã biết và ẩn để lập bài toán quy hoạch tuyến tính.
‒ Giải bài toán quy hoạch tuyến tính:
Bước 1: Biểu diễn tập phương án của bài toán trên mặt phẳng toạ độ \(Oxy\).
Bước 2: Tính giá trị của biểu thức \(F\) tại các đỉnh của \({\Omega }\).
Trong trường hợp tập phương án là miền đa giác thì giá trị lớn nhất (nhỏ nhất) trong các giá trị này là giá trị lớn nhất (nhỏ nhất) của \(F\) trên \({\Omega }\).
Trong trường hợp tập phương án không là miền đa giác nằm trong góc phần tư thứ nhất và các hệ số \(a\) và \(b\) không âm thì giá trị nhỏ nhất trong các giá trị này là giá trị nhỏ nhất của \(F\) trên \({\Omega }\).
Lời giải chi tiết:
a) Gọi \(x,y\) tấn \(\left( {x \ge 0,y \ge 0} \right)\) lần lượt là khối lượng trái cây loại A và B được thương nhân thu mua.
Thương nhân đó mua tối đa 8 tấn trái cây nên ta có phương trình sau: \(x + y \le 8\).
Số tiền mua loại trái cây A là \(12{\rm{x}}\) triệu đồng.
Số tiền mua loại trái cây B là \(20{\rm{y}}\) triệu đồng.
Tổng số tiền mua trái cây không vượt quá 120 triệu đồng nên ta có phương trình sau: \(12{\rm{x}} + 20y \le 120\) hay \(3{\rm{x}} + 5y \le 30\).
Do đó ta có hệ bất phương trình sau: \(\left\{ \begin{array}{l}x + y \le 8\\3x + 5y \le 30\\x \ge 0\\y \ge 0\end{array} \right.\).
Lợi nhuận khi bán trái cây loại A là \(1,1{\rm{x}}\) triệu đồng.
Lợi nhuận khi bán trái cây loại B là \(1,5y\) triệu đồng.
Lợi nhuận thương nhân đó thu được là: \(F = 1,1{\rm{x}} + 1,5y\) triệu đồng.
b) Ta cần giải bài toán quy hoạch tuyến tính: \(F = 1,1x + 1,5y \to \max \), với ràng buộc \(\left\{ \begin{array}{l}x + y \le 8\\3x + 5y \le 30\\x \ge 0\\y \ge 0\end{array} \right.\)
Tập phương án \({\Omega }\) là miền tứ giác \(ABCD\).
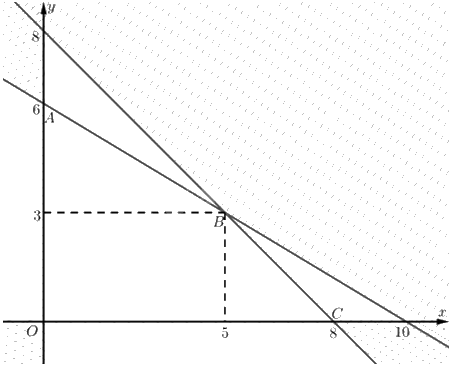
Toạ độ \(A\) là nghiệm của hệ \(\left\{ \begin{array}{l}3{\rm{x}} + 5y = 30\\x = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 0\\y = 6\end{array} \right.\). Vậy \(A\left( {0;6} \right)\).
Toạ độ \(B\) là nghiệm của hệ \(\left\{ \begin{array}{l}3{\rm{x}} + 5y = 30\\x + y = 8\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 5\\y = 3\end{array} \right.\). Vậy \(B\left( {5;3} \right)\).
Toạ độ \(C\) là nghiệm của hệ \(\left\{ \begin{array}{l}x + y = 8\\y = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 8\\y = 0\end{array} \right.\). Vậy \(C\left( {8;0} \right)\)
Giá trị của biểu thức \(F\) tại các đỉnh của \({\Omega }\):
\(\begin{array}{l}F\left( {0;0} \right) = 1,1\,.0 + 1,5\,.0 = 0;F\left( {0;6} \right) = 1,1\,.0 + 1,5\,.6 = 9;\\F\left( {5;3} \right) = 1,1\,.5 + 1,5\,.3 = 10;F\left( {8;0} \right) = 1,1\,.8 + 1,5\,.0 = 8,8\end{array}\)
Do đó: \(\mathop {\max }\limits_{\Omega } F = F\left( {5;3} \right) = 10\).
Vậy thương nhân cần mua 5 tấn loại A và 3 tấn loại B thì thu được lợi nhuận cao nhất.
Trả lời câu hỏi Thực hành 3 trang 13 Chuyên đề học tập Toán 12 Chân trời sáng tạo
Một dây chuyền của nhà máy sản xuất đá xây dựng dự định sản xuất hai loại sản phẩm A và B. Thời gian để dây chuyền sản xuất 100 tấn sản phẩm loại A và 100 tấn sản phẩm loại B lần lượt là 2 giờ và 3 giờ. Do nhu cầu thị trường, xí nghiệp sản xuất sản lượng sản phẩm loại A không ít hơn 3 lần sản lượng sản phẩm loại B. Sản phẩm loại A cho lợi nhuận là 5 triệu đồng/100 tấn; sản phẩm loại B cho lợi nhuận 9 triệu đồng/100 tấn.
Trong thời gian không quá 6 giờ làm việc của dây chuyền, cần sản xuất bao nhiêu tấn sản phẩm loại A, bao nhiêu tấn sản phẩm loại B để thu được lợi nhuận cao nhất?

Phương pháp giải:
Bước 1: Đặt hai ẩn biểu thị hai đại lượng chưa biết (cần tìm). Viết điều kiện có nghĩa cho các ẩn đó.
Bước 2: Từ dữ kiện của bài toán, viết biểu thức biểu thị đại lượng cần tìm giá trị tối ưu và các bất phương trình bậc nhất đối với hai ẩn trên. Từ đó phát biểu bài toán quy hoạch tuyến tính nhận được.
Bước 3: Giải bài toán quy hoạch tuyến tính và trả lời.
Lời giải chi tiết:
Gọi \(x,y\) tấn \(\left( {x \ge 0,y \ge 0} \right)\) lần lượt là sản lượng sản phẩm loại A và loại B xí nghiệp đó sản xuất.
Do thời gian làm việc của dây chuyền không quá 6 giờ nên \(2x + 3y \le 6\) hay \(2x + 3y - 6 \le 0\).
Do sản lượng sản phẩm loại A không ít hơn 3 lần sản lượng sản phẩm B nên \(x \ge 3y\) hay \(x - 3y \ge 0\).
Lợi nhuận thu được là \(F = 5x + 9y\) (triệu đồng).
Từ đó, ta cần giải bài toán quy hoạch tuyến tính: \(F = 5x + 9y \to \max \) với ràng buộc \(\left\{ \begin{array}{l}2x + 3y - 6 \le 0\\x - 3y \ge 0\\x \ge 0\\y \ge 0\end{array} \right.\)
Tập phương án \({\Omega }\) là miền tam giác \(OAB\).
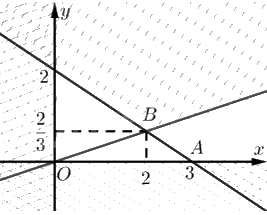
Toạ độ \(A\) là nghiệm của hệ \(\left\{ \begin{array}{l}2{\rm{x}} + 3y = 6\\y = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 3\\y = 0\end{array} \right.\). Vậy \(A\left( {3;0} \right)\).
Toạ độ \(B\) là nghiệm của hệ \(\left\{ \begin{array}{l}2{\rm{x}} + 3y = 6\\x - 3y = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = \frac{2}{3}\end{array} \right.\). Vậy \(B\left( {2;\frac{2}{3}} \right)\).
Giá trị của biểu thức \(F\) tại các đỉnh của \({\Omega }\):
\(F\left( {0;0} \right) = 5.0 + 9.0 = 0;F\left( {3;0} \right) = 5.3 + 9.0 = 15;F\left( {2;\frac{2}{3}} \right) = 5.2 + 9.\frac{2}{3} = 16\)
Do đó: \(\mathop {\max }\limits_{\Omega } F = F\left( {2;\frac{2}{3}} \right) = 16\).
Vậy xí nghiệp cần sản xuất 200 tấn loại A và \(\frac{{200}}{3}\) tấn loại B thì thu được lợi nhuận cao nhất.
Trả lời câu hỏi Thực hành 4 trang 13 Chuyên đề học tập Toán 12 Chân trời sáng tạo
Trong 100 g thịt bò loại I có chứa 21 g protein và 3,5 g lipid; 100 g thịt bò loại II có chứa 18 g protein và 10,5 g lipid. Biết rằng thịt bò loại I có giá 220 nghìn đồng/kg thì thịt bò loại II có giá 210 nghìn đồng/kg. Để có lượng thực phẩm từ hai loại thịt bò trên cung cấp ít nhất 630 g protein và 210 g lipid, cần mua khối lượng bao nhiêu cho mỗi loại thịt bò loại I và II sao cho chi phí thấp nhất?
Phương pháp giải:
Bước 1: Đặt hai ẩn biểu thị hai đại lượng chưa biết (cần tìm). Viết điều kiện có nghĩa cho các ẩn đó.
Bước 2: Từ dữ kiện của bài toán, viết biểu thức biểu thị đại lượng cần tìm giá trị tối ưu và các bất phương trình bậc nhất đối với hai ẩn trên. Từ đó phát biểu bài toán quy hoạch tuyến tính nhận được.
Bước 3: Giải bài toán quy hoạch tuyến tính và trả lời.
Lời giải chi tiết:
Gọi \(x,y\) (\(x \ge 0,y \ge 0\), tính theo 100g) lần lượt là khối lượng của thịt bò loại I và loại II cần dùng.
Do cần cung cấp ít nhất 630g protein nên ta có \(21x + 18y \ge 630\) hay \(7x + 6y - 210 \ge 0\).
Do cần cung cấp ít nhất 210g lipid nên ta có \(3,5x + 10,5y \ge 210\) hay \(x + 3y - 60 \ge 0\).
Ta có: 220 nghìn đồng/kg=22 nghìn đồng/100g; 210 nghìn đồng/kg=21 nghìn đồng/100g.
Chi phí để mua thịt bò là \(F = 22x + 21y\) (nghìn đồng).
Từ đó, ta cần giải bài toán quy hoạch tuyến tính: \(F = 22x + 21y \to \min \) với ràng buộc \(\left\{ \begin{array}{l}7{\rm{x}} + 6y - 210 \ge 0\\x + 3y - 60 \ge 0\\x \ge 0\\y \ge 0\end{array} \right.\)
Tập phương án \({\Omega }\) của bài toán là miền không gạch (không là miền đa giác).
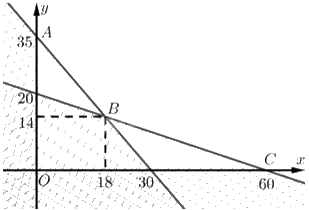
Toạ độ \(A\) là nghiệm của hệ \(\left\{ \begin{array}{l}7{\rm{x}} + 6y = 210\\x = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 0\\y = 35\end{array} \right.\). Vậy \(A\left( {0;35} \right)\).
Toạ độ \(B\) là nghiệm của hệ \(\left\{ \begin{array}{l}7{\rm{x}} + 6y = 210\\x + 3y = 60\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 18\\y = 14\end{array} \right.\). Vậy \(B\left( {18;14} \right)\).
Toạ độ \(C\) là nghiệm của hệ \(\left\{ \begin{array}{l}x + 3y = 60\\y = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 60\\y = 0\end{array} \right.\). Vậy \(C\left( {60;0} \right)\).
Giá trị của biểu thức \(F\) tại các đỉnh của \({\Omega }\):
\(F\left( {0;35} \right) = 22.0 + 21.35 = 735;F\left( {18;14} \right) = 22.18 + 21.14 = 690;F\left( {60;0} \right) = 22.60 + 21.0 = 1320\)
Do đó: \(\mathop {\min }\limits_{\Omega } F = F\left( {18;14} \right) = 690\).
Vậy cần mua \(18.100g = 1,8kg\) thịt bò loại I và \(14.100g = 1,4kg\) thịt bò loại II.
Mục 2 của Chuyên đề học tập Toán 12 - Chân trời sáng tạo thường tập trung vào một chủ đề cụ thể trong chương trình. Việc nắm vững kiến thức và kỹ năng trong mục này là rất quan trọng để giải quyết các bài toán phức tạp hơn trong các phần tiếp theo. Bài viết này sẽ cung cấp lời giải chi tiết cho từng bài tập trong mục 2 trang 11, 12, 13, đồng thời giải thích rõ ràng các bước thực hiện và các khái niệm liên quan.
(Giả sử bài tập 1 là một bài toán về giới hạn)
Để giải bài tập này, chúng ta cần áp dụng định nghĩa về giới hạn của một hàm số tại một điểm. Cụ thể, ta cần chứng minh rằng với mọi số dương ε (epsilon) nhỏ tùy ý, tồn tại một số dương δ (delta) sao cho nếu 0 < |x - a| < δ thì |f(x) - L| < ε. Trong bài toán này, a là điểm ta tính giới hạn, L là giá trị giới hạn, và f(x) là hàm số cần tính giới hạn.
Lời giải:
(Giả sử bài tập 2 là một bài toán về đạo hàm)
Để giải bài tập này, chúng ta cần sử dụng các quy tắc tính đạo hàm cơ bản, bao gồm đạo hàm của tổng, hiệu, tích, thương, và đạo hàm của hàm hợp. Ngoài ra, cần nhớ các đạo hàm của các hàm số sơ cấp như sin(x), cos(x), ex, ln(x), v.v.
Lời giải:
(Giả sử bài tập 3 là một bài toán về tích phân)
Để giải bài tập này, chúng ta cần sử dụng các phương pháp tính tích phân cơ bản, bao gồm tích phân từng phần, đổi biến số, và sử dụng các công thức tích phân đã biết. Ngoài ra, cần chú ý đến các điều kiện để áp dụng các phương pháp này.
Lời giải:
Sử dụng phương pháp đổi biến số u = g(x), suy ra du = g'(x)dx. Thay thế vào tích phân ban đầu, ta được một tích phân mới theo biến u. Giải tích phân mới này, sau đó thay u = g(x) trở lại để có kết quả cuối cùng.
Ngoài sách giáo khoa, các em có thể tham khảo thêm các tài liệu sau:
Hy vọng rằng bài viết này đã cung cấp cho các em những kiến thức và kỹ năng cần thiết để giải quyết các bài tập trong mục 2 trang 11, 12, 13 Chuyên đề học tập Toán 12 - Chân trời sáng tạo. Chúc các em học tập tốt và đạt kết quả cao trong kỳ thi sắp tới!