Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 12. Bài viết này sẽ hướng dẫn bạn giải bài 8 trang 22 thuộc Chuyên đề học tập Toán 12 - Chân trời sáng tạo một cách nhanh chóng và hiệu quả.
Chúng tôi cam kết mang đến cho bạn những giải pháp học tập tốt nhất, giúp bạn nắm vững kiến thức và tự tin hơn trong các kỳ thi.
Thức ăn chăn nuôi A gồm 60% bột ngô và 40% bột đậu nành, thức ăn chăn nuôi B gồm 80% bột ngô và 20% bột đậu nành. Hiện tại xí nghiệp sản xuất chỉ còn 2,4 tấn bột ngô và 1,2 tấn bột đậu nành. Với số nguyên liệu này, xí nghiệp đó nên sản xuất khối lượng bao nhiêu mỗi loại sản phẩm A và B để thu được lợi nhuận cao nhất? Biết rằng A cho lợi nhuận 2 triệu đồng/tấn và B cho lợi nhuận 1,8 triệu đồng/tấn.
Đề bài
Thức ăn chăn nuôi A gồm 60% bột ngô và 40% bột đậu nành, thức ăn chăn nuôi B gồm 80% bột ngô và 20% bột đậu nành. Hiện tại xí nghiệp sản xuất chỉ còn 2,4 tấn bột ngô và 1,2 tấn bột đậu nành. Với số nguyên liệu này, xí nghiệp đó nên sản xuất khối lượng bao nhiêu mỗi loại sản phẩm A và B để thu được lợi nhuận cao nhất? Biết rằng A cho lợi nhuận 2 triệu đồng/tấn và B cho lợi nhuận 1,8 triệu đồng/tấn.
Phương pháp giải - Xem chi tiết
Bước 1: Đặt hai ẩn biểu thị hai đại lượng chưa biết (cần tìm). Viết điều kiện có nghĩa cho các ẩn đó.
Bước 2: Từ dữ kiện của bài toán, viết biểu thức biểu thị đại lượng cần tìm giá trị tối ưu và các bất phương trình bậc nhất đối với hai ẩn trên. Từ đó phát biểu bài toán quy hoạch tuyến tính nhận được.
Bước 3: Giải bài toán quy hoạch tuyến tính và trả lời.
Lời giải chi tiết
Gọi \(x,y\left( {x \ge 0,y \ge 0} \right)\) lần lượt là số tấn sản phẩm A và B được sản xuất.
Xí nghiệp sản xuất chỉ còn 2,4 tấn bột ngô nên ta có \(0,6x + 0,8y \le 2,4\) hay \(3x + 4y - 12 \le 0\).
Xí nghiệp sản xuất chỉ còn 1,2 tấn bột đậu nành nên ta có \(0,4x + 0,2y \le 1,2\) hay \(2x + y - 6 \le 0\).
Lợi nhuận thu được là \(F = 2x + 1,8y\) (triệu đồng).
Từ đó, ta cần giải bài toán quy hoạch tuyến tính: \(F = 2x + 1,8y \to \max \) với ràng buộc \(\left\{ \begin{array}{l}3x + 4y - 12 \le 0\\2x + y - 6 \le 0\\x \ge 0\\y \ge 0\end{array} \right.\)
Tập phương án \({\Omega }\) là miền tứ giác \(OABC\).
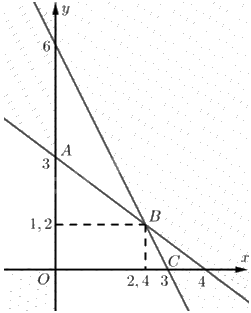
Ta có \(A\left( {0;3} \right),C\left( {3;0} \right)\).
Toạ độ \(B\) là nghiệm của hệ \(\left\{ \begin{array}{l}3x + 4y - 12 \le 0\\2x + y - 6 \le 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2,4\\y = 1,2\end{array} \right.\). Vậy \(B\left( {2,4;1,2} \right)\).
Giá trị của biểu thức \(F\) tại các đỉnh của \({\Omega }\):
\(F\left( {0;0} \right) = 0;F\left( {0;3} \right) = 5,4;F\left( {2,4;1,2} \right) = 6,96;F\left( {3;0} \right) = 6\)
Do đó: \(\mathop {\max }\limits_{\Omega } F = F\left( {2,4;1,2} \right) = 6,96\).
Vậy để thu được nhiều lợi nhuận nhất thì nhà sản xuất cần sản xuất 2,4 tấn sản phẩm A và 1,2 tấn sản phẩm B.
Bài 8 trang 22 Chuyên đề học tập Toán 12 - Chân trời sáng tạo thuộc chương trình học Toán 12, tập trung vào việc vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế liên quan đến sự biến thiên của hàm số. Bài tập này yêu cầu học sinh phải nắm vững các khái niệm về đạo hàm, cực trị, và khoảng đơn điệu của hàm số.
Bài 8 thường bao gồm các dạng bài tập sau:
Để giải bài 8 trang 22 Chuyên đề học tập Toán 12 - Chân trời sáng tạo một cách hiệu quả, bạn có thể áp dụng các bước sau:
Bài toán: Tìm khoảng đơn điệu của hàm số y = x3 - 3x2 + 2.
Giải:
Kết luận: Hàm số y = x3 - 3x2 + 2 đồng biến trên (-∞, 0) và (2, +∞), nghịch biến trên (0, 2).
Để học tập và ôn luyện hiệu quả, bạn có thể tham khảo các tài liệu sau:
Bài 8 trang 22 Chuyên đề học tập Toán 12 - Chân trời sáng tạo là một bài tập quan trọng giúp bạn củng cố kiến thức về đạo hàm và ứng dụng của nó. Hy vọng với hướng dẫn chi tiết và ví dụ minh họa trên, bạn sẽ tự tin hơn trong việc giải quyết bài tập này và đạt kết quả tốt trong các kỳ thi.