Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài 4 trang 21 Chuyên đề học tập Toán 12 - Chân trời sáng tạo. Bài viết này cung cấp đáp án đầy đủ, phương pháp giải rõ ràng, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Chúng tôi luôn cố gắng cung cấp nội dung chất lượng, dễ hiểu, phù hợp với chương trình học Toán 12 hiện hành. Hãy cùng giaitoan.edu.vn khám phá lời giải bài tập này nhé!
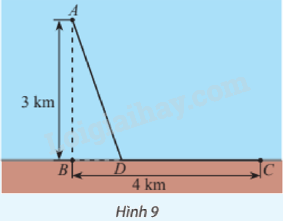
Một giếng dầu ngoài khơi được đặt ở vị trí \(A\) cách bờ biển 3 km, \(B\) là vị trí trên bờ biển gần giếng dầu nhất. Nhà máy lọc dầu được đặt ở vị trí \(C\) trên bờ biển, cách vị trí \(B\) một khoảng 4 km (Hình 9). Người ta dự định lắp đặt đường ống dẫn dầu gồm hai đoạn thẳng \(AD\) và \(DC\) (\(D\) là một vị trí nằm giữa \(B\) và \(C\)). Biết rằng mỗi mét đường ống đặt dưới biển có chi phí lắp đặt cao gấp đôi so với mỗi mét đường ống đặt trên bờ. Vị trí của \(D\) như thế nào để giảm thiểu chi p
Đề bài
Một giếng dầu ngoài khơi được đặt ở vị trí \(A\) cách bờ biển 3 km, \(B\) là vị trí trên bờ biển gần giếng dầu nhất. Nhà máy lọc dầu được đặt ở vị trí \(C\) trên bờ biển, cách vị trí \(B\) một khoảng 4 km (Hình 9). Người ta dự định lắp đặt đường ống dẫn dầu gồm hai đoạn thẳng \(AD\) và \(DC\) (\(D\) là một vị trí nằm giữa \(B\) và \(C\)). Biết rằng mỗi mét đường ống đặt dưới biển có chi phí lắp đặt cao gấp đôi so với mỗi mét đường ống đặt trên bờ. Vị trí của \(D\) như thế nào để giảm thiểu chi phí lắp đặt nhất?
Phương pháp giải - Xem chi tiết
• Đặt \(BD = x\), biểu thị chi phí lắp đặt thông qua các đại lượng đã biết và ẩn.
• Cách tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số \(f\left( x \right)\) trên đoạn \(\left[ {a;b} \right]\):
Bước 1. Tìm các điểm \({x_1},{x_2},...,{x_n}\) thuộc khoảng \(\left( {a;b} \right)\) mà tại đó \(f'\left( x \right)\) bằng 0 hoặc không tồn tại.
Bước 2. Tính \(f\left( a \right);f\left( {{x_1}} \right);f\left( {{x_2}} \right);...;f\left( {{x_n}} \right);f\left( b \right)\).
Bước 3. Gọi \(M\) là số lớn nhất và \(m\) là số nhỏ nhất trong các giá trị tìm được ở Bước 2. Khi đó: \(M = \mathop {\max }\limits_{\left[ {a;b} \right]} f\left( x \right),m = \mathop {\min }\limits_{\left[ {a;b} \right]} f\left( x \right)\).
Lời giải chi tiết
Đặt \(BD = x\left( {km} \right)\left( {0 \le x \le 4} \right)\).
Gọi \(a\) là chi phí lắp đặt cho mỗi kilômét đường ống đặt trên bờ.
Khi đó \(2a\) là chi phí lắp đặt cho mỗi kilômét đường ống đặt dưới biển.
Ta có: \(C{\rm{D}} = BC - B{\rm{D}} = 4 - x,A{\rm{D}} = \sqrt {A{B^2} + B{{\rm{D}}^2}} = \sqrt {{x^2} + 9} \).
Chi phí lắp đặt đường ống là: \(2{\rm{a}}\sqrt {{x^2} + 9} + a\left( {4 - x} \right) = a\left( {2\sqrt {{x^2} + 9} + 4 - x} \right)\).
Xét hàm số \(f\left( x \right) = 2\sqrt {{x^2} + 9} + 4 - x\) trên đoạn \(\left[ {0;4} \right]\).
Ta có: \(f'\left( x \right) = 2.\frac{{{{\left( {{x^2} + 9} \right)}^\prime }}}{{2\sqrt {{x^2} + 9} }} - 1 = \frac{{2{\rm{x}}}}{{\sqrt {{x^2} + 9} }} - 1\)
\(f'\left( x \right) = 0 \Leftrightarrow \frac{{2{\rm{x}}}}{{\sqrt {{x^2} + 9} }} - 1 = 0 \Leftrightarrow \frac{{2{\rm{x}}}}{{\sqrt {{x^2} + 9} }} = 1 \Leftrightarrow \sqrt {{x^2} + 9} = 2{\rm{x}} \Leftrightarrow {x^2} + 9 = 4{{\rm{x}}^2} \Leftrightarrow {{\rm{x}}^2} = 3 \Leftrightarrow x = \sqrt 3 \) hoặc \(x = - \sqrt 3 \) (loại).
\(f\left( 0 \right) = 10;f\left( {\sqrt 3 } \right) = 4 + 3\sqrt 3 ;f\left( 4 \right) = 10\).
Vậy \(\mathop {\min }\limits_{\left[ {0;4} \right]} f\left( x \right) = f\left( {\sqrt 3 } \right) = 4 + 3\sqrt 3 \).
Vậy chi phí lắp đặt thấp nhất khi \(x = \sqrt 3 \approx 1,7\left( {km} \right)\).
Bài 4 trang 21 Chuyên đề học tập Toán 12 - Chân trời sáng tạo thuộc chương trình học về đạo hàm. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm của hàm số, đặc biệt là đạo hàm của các hàm số lượng giác và hàm hợp để giải quyết các bài toán thực tế.
Bài 4 thường xoay quanh việc tính đạo hàm của hàm số, tìm điểm cực trị, khảo sát hàm số và ứng dụng đạo hàm để giải các bài toán liên quan đến tối ưu hóa. Cụ thể, bài tập có thể yêu cầu:
Để giải bài 4 trang 21 Chuyên đề học tập Toán 12 - Chân trời sáng tạo, học sinh cần nắm vững các kiến thức và kỹ năng sau:
Dưới đây là lời giải chi tiết cho từng phần của bài 4 trang 21 Chuyên đề học tập Toán 12 - Chân trời sáng tạo:
Áp dụng quy tắc đạo hàm của hàm hợp, ta có:
f'(x) = (sin(2x))' + (cos(x))' = cos(2x) * 2 - sin(x) = 2cos(2x) - sin(x)
Tính đạo hàm bậc nhất: g'(x) = 3x^2 - 6x
Giải phương trình g'(x) = 0: 3x^2 - 6x = 0 => x(x - 2) = 0 => x = 0 hoặc x = 2
Tính đạo hàm bậc hai: g''(x) = 6x - 6
Kiểm tra điều kiện cực trị:
Vậy hàm số g(x) có điểm cực đại là (0, 2) và điểm cực tiểu là (2, -2).
Tập xác định: D = R \ {-1}
Đạo hàm: h'(x) = (x+1 - (x-1))/(x+1)^2 = 2/(x+1)^2 > 0 với mọi x ≠ -1
Hàm số đồng biến trên các khoảng (-∞, -1) và (-1, +∞)
Giới hạn: lim(x→∞) h(x) = 1, lim(x→-∞) h(x) = 1, lim(x→-1+) h(x) = +∞, lim(x→-1-) h(x) = -∞
Đồ thị hàm số có tiệm cận ngang y = 1 và tiệm cận đứng x = -1
(Ví dụ cụ thể về bài toán tối ưu hóa và lời giải chi tiết sẽ được trình bày tại đây)
Bài 4 trang 21 Chuyên đề học tập Toán 12 - Chân trời sáng tạo là một bài tập quan trọng giúp học sinh củng cố kiến thức về đạo hàm và ứng dụng của đạo hàm trong việc giải quyết các bài toán thực tế. Hy vọng với lời giải chi tiết và phương pháp giải rõ ràng trên đây, các em học sinh sẽ tự tin hơn trong quá trình học tập và làm bài.