Giải bài 1 trang 21 Chuyên đề học tập Toán 12 - Chân trời sáng tạo

Chào mừng các em học sinh đến với lời giải chi tiết bài 1 trang 21 Chuyên đề học tập Toán 12 - Chân trời sáng tạo. Bài viết này được cung cấp bởi giaitoan.edu.vn, với mục tiêu hỗ trợ các em học tập và ôn luyện môn Toán hiệu quả.

Chúng tôi sẽ trình bày lời giải từng bước, rõ ràng, dễ hiểu, giúp các em nắm vững kiến thức và kỹ năng giải bài tập.

Giá trị lớn nhất của biểu thức (Fleft( {x;y} right) = 5x - 2y) trên miền ({Omega }) ở Hình 1 là A. 3. B. 22. C. 18. D. 20.

Đề bài

Giá trị lớn nhất của biểu thức \(F\left( {x;y} \right) = 5x - 2y\) trên miền \({\Omega }\) ở Hình 1 là

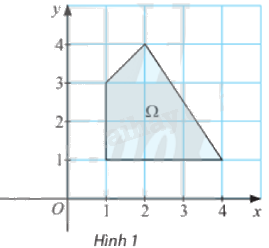
A. 3.

B. 22.

C. 18.

D. 20.

Phương pháp giải - Xem chi tiết Giải bài 1 trang 21 Chuyên đề học tập Toán 12 - Chân trời sáng tạo 2

Trong trường hợp tập phương án là miền đa giác thì giá trị lớn nhất (nhỏ nhất) trong các giá trị này là giá trị lớn nhất (nhỏ nhất) của \(F\) trên \({\Omega }\).

Lời giải chi tiết

Giá trị của biểu thức \(F\) tại các đỉnh của \({\Omega }\):

\(F\left( {1;1} \right) = 3;F\left( {1;3} \right) = - 1;F\left( {4;1} \right) = 18;F\left( {2;4} \right) = 2\)

Do đó: \(\mathop {\max }\limits_{\Omega } F = F\left( {4;1} \right) = 18\).

Chọn C

Tự tin bứt phá Kỳ thi THPT Quốc gia môn Toán! Đừng bỏ lỡ Giải bài 1 trang 21 Chuyên đề học tập Toán 12 - Chân trời sáng tạo đặc sắc thuộc chuyên mục toán lớp 12 trên nền tảng toán math. Với bộ bài tập toán thpt được biên soạn chuyên sâu, bám sát cấu trúc đề thi và chương trình Toán 12, đây chính là "chiến lược vàng" giúp các em tối ưu hóa ôn luyện. Học sinh sẽ không chỉ làm chủ mọi dạng bài thi mà còn nắm vững chiến thuật làm bài hiệu quả, sẵn sàng tự tin chinh phục điểm cao, vững bước vào đại học mơ ước nhờ phương pháp học trực quan, khoa học và hiệu quả học tập vượt trội!

Giải bài 1 trang 21 Chuyên đề học tập Toán 12 - Chân trời sáng tạo: Tổng quan

Bài 1 trang 21 Chuyên đề học tập Toán 12 - Chân trời sáng tạo thuộc chương trình học Toán 12, tập trung vào việc ôn tập và củng cố kiến thức về đạo hàm. Bài tập này yêu cầu học sinh vận dụng các kiến thức về đạo hàm của hàm số, quy tắc tính đạo hàm, và ứng dụng của đạo hàm để giải quyết các bài toán cụ thể.

Nội dung bài tập

Bài 1 thường bao gồm các dạng bài tập sau:

Tính đạo hàm của hàm số tại một điểm.
Tìm đạo hàm của hàm số.
Ứng dụng đạo hàm để xét tính đơn điệu của hàm số.
Ứng dụng đạo hàm để tìm cực trị của hàm số.

Lời giải chi tiết bài 1 trang 21

Để giải bài 1 trang 21 Chuyên đề học tập Toán 12 - Chân trời sáng tạo, chúng ta cần thực hiện các bước sau:

Xác định hàm số: Đọc kỹ đề bài để xác định chính xác hàm số cần tính đạo hàm hoặc phân tích.
Chọn quy tắc tính đạo hàm phù hợp: Dựa vào cấu trúc của hàm số, chọn quy tắc tính đạo hàm phù hợp (quy tắc đạo hàm của tổng, hiệu, tích, thương, hàm hợp, v.v.).
Tính đạo hàm: Áp dụng quy tắc đã chọn để tính đạo hàm của hàm số.
Rút gọn kết quả: Rút gọn biểu thức đạo hàm để có kết quả cuối cùng.
Kiểm tra lại: Kiểm tra lại kết quả để đảm bảo tính chính xác.

Ví dụ minh họa

Ví dụ: Tính đạo hàm của hàm số f(x) = x² + 2x - 1.

Lời giải:

f'(x) = (x²)' + (2x)' - (1)' = 2x + 2 - 0 = 2x + 2.

Mở rộng kiến thức

Để hiểu sâu hơn về đạo hàm và ứng dụng của đạo hàm, các em có thể tham khảo thêm các tài liệu sau:

Sách giáo khoa Toán 12 - Chân trời sáng tạo.
Sách bài tập Toán 12 - Chân trời sáng tạo.
Các trang web học toán online uy tín.

Lưu ý khi giải bài tập

Khi giải bài tập về đạo hàm, các em cần lưu ý những điều sau:

Nắm vững các quy tắc tính đạo hàm cơ bản.
Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.
Kiểm tra lại kết quả để đảm bảo tính chính xác.
Sử dụng máy tính bỏ túi để kiểm tra kết quả (nếu cần thiết).

Ứng dụng của đạo hàm trong thực tế

Đạo hàm có rất nhiều ứng dụng trong thực tế, ví dụ như:

Tính vận tốc và gia tốc trong vật lý.
Tìm cực trị của hàm số trong kinh tế.
Phân tích sự thay đổi của các hiện tượng tự nhiên.

Tổng kết

Bài 1 trang 21 Chuyên đề học tập Toán 12 - Chân trời sáng tạo là một bài tập quan trọng giúp các em củng cố kiến thức về đạo hàm. Hy vọng với lời giải chi tiết và những lưu ý trên, các em sẽ giải bài tập này một cách dễ dàng và hiệu quả. Chúc các em học tập tốt!