Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài 7 trang 22 Chuyên đề học tập Toán 12 - Chân trời sáng tạo. Bài viết này cung cấp đáp án đầy đủ, phương pháp giải rõ ràng, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Chúng tôi luôn cố gắng cung cấp nội dung chất lượng, dễ hiểu, phù hợp với chương trình học Toán 12 hiện hành. Hãy cùng giaitoan.edu.vn khám phá lời giải bài tập này nhé!
Giải bài toán quy hoạch tuyến tính: \(F = 3x + 5y \to \min \) với ràng buộc \(\left\{ \begin{array}{l}2{\rm{x}} - y + 4 \ge 0\\4{\rm{x}} + 3y \ge 12\\2{\rm{x}} - 3y \le 6\end{array} \right.\)
Đề bài
Giải bài toán quy hoạch tuyến tính:
\(F = 3x + 5y \to \min \)
với ràng buộc
\(\left\{ \begin{array}{l}2{\rm{x}} - y + 4 \ge 0\\4{\rm{x}} + 3y \ge 12\\2{\rm{x}} - 3y \le 6\end{array} \right.\)
Phương pháp giải - Xem chi tiết
Bước 1: Biểu diễn tập phương án của bài toán trên mặt phẳng toạ độ \(Oxy\).
Bước 2: Tính giá trị của biểu thức \(F\) tại các đỉnh của \({\Omega }\).
Trong trường hợp tập phương án là miền đa giác thì giá trị lớn nhất (nhỏ nhất) trong các giá trị này là giá trị lớn nhất (nhỏ nhất) của \(F\) trên \({\Omega }\).
Trong trường hợp tập phương án không là miền đa giác nằm trong góc phần tư thứ nhất và các hệ số \(a\) và \(b\) không âm thì giá trị nhỏ nhất trong các giá trị này là giá trị nhỏ nhất của \(F\) trên \({\Omega }\).
Lời giải chi tiết
Viết lại ràng buộc
\(\left\{ \begin{array}{l}2{\rm{x}} - y \ge - 4\\4{\rm{x}} + 3y \ge 12\\2{\rm{x}} - 3y \le 6\end{array} \right.\)
Tập phương án \({\Omega }\) của bài toán là miền không gạch (không là miền đa giác).
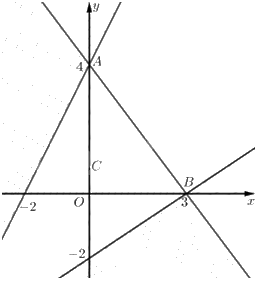
Ta có \(A\left( {0;4} \right),B\left( {3;0} \right)\).
Do \({\Omega }\) nằm trong góc phần tư thứ nhất và các hệ số của biểu thức \(F = 3x + 5y\) đều dương nên \(F\) đạt giá trị nhỏ nhất tại một đỉnh của \({\Omega }\).
Ta có \(F\left( {0;4} \right) = 40,F\left( {3;0} \right) = 9\).
Do đó \(\mathop {\min }\limits_{\Omega } F = F\left( {3;0} \right) = 9\).
Bài 7 trang 22 Chuyên đề học tập Toán 12 - Chân trời sáng tạo thuộc chương trình học về đạo hàm. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm của hàm số, đặc biệt là đạo hàm của các hàm số lượng giác và hàm hợp để giải quyết các bài toán thực tế.
Bài 7 thường bao gồm các dạng bài tập sau:
Để giải bài 7 trang 22 Chuyên đề học tập Toán 12 - Chân trời sáng tạo hiệu quả, học sinh cần nắm vững các kiến thức và kỹ năng sau:
Bài 7a: Tính đạo hàm của hàm số y = sin(2x + 1)
Lời giải:
Sử dụng quy tắc hàm hợp: y' = (sin(2x + 1))' = cos(2x + 1) * (2x + 1)' = 2cos(2x + 1)
Bài 7b: Tính đạo hàm của hàm số y = x2 * cos(x)
Lời giải:
Sử dụng quy tắc nhân: y' = (x2)' * cos(x) + x2 * (cos(x))' = 2x * cos(x) - x2 * sin(x)
Bài 7c: Tìm đạo hàm cấp hai của hàm số y = ex * sin(x)
Lời giải:
y' = (ex)' * sin(x) + ex * (sin(x))' = ex * sin(x) + ex * cos(x)
y'' = (ex * sin(x))' + (ex * cos(x))' = ex * sin(x) + ex * cos(x) + ex * cos(x) - ex * sin(x) = 2ex * cos(x)
Học sinh có thể tham khảo thêm các tài liệu sau để hiểu rõ hơn về đạo hàm:
Bài 7 trang 22 Chuyên đề học tập Toán 12 - Chân trời sáng tạo là một bài tập quan trọng giúp học sinh củng cố kiến thức về đạo hàm. Hy vọng với lời giải chi tiết và phương pháp giải rõ ràng trên đây, các em học sinh sẽ tự tin giải quyết bài tập này và đạt kết quả tốt trong môn Toán.