Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho bài tập Toán 12. Bài viết này sẽ hướng dẫn bạn giải bài 4 trang 64 Chuyên đề học tập Toán 12 - Chân trời sáng tạo một cách nhanh chóng và hiệu quả.
Chúng tôi cam kết mang đến cho bạn những giải pháp học tập tốt nhất, giúp bạn nắm vững kiến thức và đạt kết quả cao trong môn Toán.
Kết quả khảo sát cân nặng (làm tròn đến 100 g) của 50 trái sầu riêng trong một lô hàng A được tổng hợp ở bảng sau: a) Chọn ngẫu nhiên 1 trái sầu riêng trong lô hàng A và gọi \(X\) là cân nặng (làm tròn đến 100 g) của trái sầu riêng đó. Hãy tính kì vọng và độ lệch chuẩn của \(X\). b) Cân nặng của một quả sầu riêng được lựa chọn ngẫu nhiên từ lô hàng B có kì vọng 2524 g và độ lệch chuẩn là 121 g. Hỏi nếu so sánh theo độ lệch chuẩn thì sầu riêng ở lô hàng nào có cân nặng đồng đều hơn?
Đề bài
Kết quả khảo sát cân nặng (làm tròn đến 100 g) của 50 trái sầu riêng trong một lô hàng A được tổng hợp ở bảng sau:
a) Chọn ngẫu nhiên 1 trái sầu riêng trong lô hàng A và gọi \(X\) là cân nặng (làm tròn đến 100 g) của trái sầu riêng đó. Hãy tính kì vọng và độ lệch chuẩn của \(X\). b) Cân nặng của một quả sầu riêng được lựa chọn ngẫu nhiên từ lô hàng B có kì vọng 2524 g và độ lệch chuẩn là 121 g. Hỏi nếu so sánh theo độ lệch chuẩn thì sầu riêng ở lô hàng nào có cân nặng đồng đều hơn?
Phương pháp giải - Xem chi tiết
Giả sử biến ngẫu nhiên rời rạc \(X\) có bảng phân bố xác suất như sau:
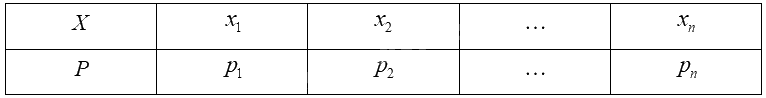
Kì vọng của \(X\) được tính bởi công thức: \(E\left( X \right) = {x_1}{p_1} + {x_2}{p_2} + ... + {x_n}{p_n}\).
Phương sai của \(X\) được tính bởi công thức: \(V\left( X \right) = x_1^2{p_1} + x_2^2{p_2} + ... + x_n^2{p_n} - {\left[ {E\left( X \right)} \right]^2}\).
Độ lệch chuẩn của \(X\) được tính bởi công thức: \(\sigma \left( X \right) = \sqrt {V\left( X \right)} \).
Lời giải chi tiết
a) Xác suất để chọn được trái sầu riêng 2400 g là: \(\frac{6}{{50}} = 0,12\).
Xác suất để chọn được trái sầu riêng 2500 g là: \(\frac{{20}}{{50}} = 0,4\).
Xác suất để chọn được trái sầu riêng 2600 g là: \(\frac{{16}}{{50}} = 0,32\).
Xác suất để chọn được trái sầu riêng 2700 g là: \(\frac{8}{{50}} = 0,16\).
Bảng phân bố xác suất của \(X\):
Kì vọng của \(X\) là: \(E\left( X \right) = 2400.0,12 + 2500.0,4 + 2600.0,32 + 2700.0,16 = 2552\).
Phương sai của \(X\) là:
\(V\left( X \right) = {2400^2}.0,12 + {2500^2}.0,4 + {2600^2}.0,32 + {2700^2}.0,16 - {2552^2} = 8096\).
Độ lệch chuẩn của \(X\) là: \(\sigma \left( X \right) = \sqrt {8096} = 4\sqrt {506} \approx 89,98\).
b) Nếu so sánh theo độ lệch chuẩn thì sầu riêng ở lô hàng A có cân nặng đồng đều hơn.
Bài 4 trang 64 Chuyên đề học tập Toán 12 - Chân trời sáng tạo thuộc chương trình học Toán 12, tập trung vào việc vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế. Bài tập này thường yêu cầu học sinh phân tích hàm số, tìm cực trị, và khảo sát sự biến thiên của hàm số. Việc nắm vững các khái niệm và kỹ năng liên quan đến đạo hàm là yếu tố then chốt để giải quyết thành công bài toán này.
Trước khi bắt đầu giải bài, điều quan trọng là phải đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Trong bài 4 trang 64, học sinh cần xác định hàm số cần khảo sát, các điểm không xác định, và các khoảng đơn điệu của hàm số. Ngoài ra, cần tìm các điểm cực trị và vẽ đồ thị hàm số để hiểu rõ hơn về tính chất của hàm số.
Để giải bài 4 trang 64, học sinh có thể áp dụng các phương pháp sau:
Giả sử hàm số cần khảo sát là f(x) = x3 - 3x2 + 2. Ta sẽ áp dụng các bước trên để giải bài toán:
Ngoài sách giáo khoa và chuyên đề học tập, học sinh có thể tham khảo thêm các tài liệu sau để hỗ trợ học tập:
Giải bài 4 trang 64 Chuyên đề học tập Toán 12 - Chân trời sáng tạo đòi hỏi học sinh phải nắm vững kiến thức về đạo hàm và áp dụng các phương pháp giải bài tập một cách linh hoạt. Hy vọng với hướng dẫn chi tiết và ví dụ minh họa trên, bạn sẽ tự tin giải quyết bài toán này một cách hiệu quả. Chúc bạn học tập tốt!
