Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 12. Bài viết này sẽ hướng dẫn bạn giải bài 3 trang 38 thuộc Chuyên đề học tập Toán 12 - Chân trời sáng tạo một cách nhanh chóng và hiệu quả.
Chúng tôi cam kết mang đến cho bạn những giải pháp học tập tốt nhất, giúp bạn nắm vững kiến thức và tự tin hơn trong các kỳ thi.
Doanh nghiệp C vay của công ty tài chính D với hợp đồng vay như sau: Số tiền vay là 500 triệu đồng, thời hạn vay 6 tháng, lãi suất cho vay 12%/năm. Tiền gốc phải trả đều mỗi tháng. Tiền lãi tính theo dư nợ giảm dần. Ngày giải ngân 01/6/2023. a) Tính số tiền gốc và lãi mà doanh nghiệp C phải trả hằng tháng. b) Tính tổng số tiền gốc và lãi mà doanh nghiệp C đã trả vào cuối kì vay.
Đề bài
Doanh nghiệp C vay của công ty tài chính D với hợp đồng vay như sau: Số tiền vay là 500 triệu đồng, thời hạn vay 6 tháng, lãi suất cho vay 12%/năm. Tiền gốc phải trả đều mỗi tháng. Tiền lãi tính theo dư nợ giảm dần. Ngày giải ngân 01/6/2023.
a) Tính số tiền gốc và lãi mà doanh nghiệp C phải trả hằng tháng.
b) Tính tổng số tiền gốc và lãi mà doanh nghiệp C đã trả vào cuối kì vay.
Phương pháp giải - Xem chi tiết
‒ Lãi đơn: \({I_n} = P.r.n\) (với \(P\): vốn gốc, \(r\): lãi suất trên một kì hạn, \(n\): số kì hạn).
‒ Giá trị cả vốn lẫn lãi sau \(n\) chu kì lãi đơn: \({F_n} = P\left( {1 + n{\rm{r}}} \right)\) (với \(P\): vốn gốc, \(r\): lãi suất trên một kì hạn, \(n\): số kì hạn).
Lời giải chi tiết
a) Do tiền lãi tính theo dư nợ ban đầu nên công ty A sẽ trả nợ ngân hàng B theo phương thức lãi đơn.
Ta có: \(P = 100,r = 9\% ,n = 1\).
Tổng số tiền gốc và lãi mà công ty A phải trả cho ngân hàng B vào cuối kì vay là:
\(100\left( {1 + 9\% } \right) = 109\) (triệu đồng).
b) Áp dụng công thức lãi đơn cho từng tháng, theo hợp đồng vay ta có bảng tính sau:
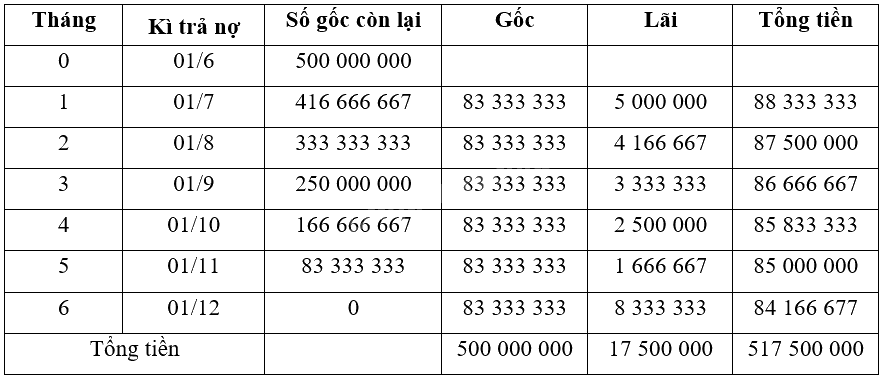
b) Tổng số tiền cả gốc và lãi mà doanh nghiệp C đã trả vào cuối kì vay là 517,5 triệu đồng.
Bài 3 trang 38 Chuyên đề học tập Toán 12 - Chân trời sáng tạo thuộc chương trình học Toán 12, tập trung vào việc vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế. Bài tập này thường yêu cầu học sinh phân tích hàm số, tìm cực trị, và khảo sát sự biến thiên của hàm số. Việc nắm vững các khái niệm và kỹ năng liên quan đến đạo hàm là vô cùng quan trọng để giải quyết bài toán này một cách hiệu quả.
Trước khi bắt đầu giải bài, chúng ta cần đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Thông thường, đề bài sẽ yêu cầu chúng ta tìm các yếu tố như:
Để giải bài 3 trang 38 Chuyên đề học tập Toán 12 - Chân trời sáng tạo, chúng ta có thể áp dụng các phương pháp sau:
Giả sử đề bài yêu cầu giải bài 3 trang 38 với hàm số f(x) = x3 - 3x2 + 2. Chúng ta sẽ tiến hành giải như sau:
Giải phương trình f'(x) = 0, ta được x = 0 hoặc x = 2.
Tại x = 0, f''(0) = -6 < 0, nên x = 0 là điểm cực đại.
Tại x = 2, f''(2) = 6 > 0, nên x = 2 là điểm cực tiểu.
Hàm số đồng biến trên các khoảng (-∞, 0) và (2, +∞).
Hàm số nghịch biến trên khoảng (0, 2).
Khi giải bài 3 trang 38 Chuyên đề học tập Toán 12 - Chân trời sáng tạo, bạn cần lưu ý những điều sau:
Việc giải bài 3 trang 38 Chuyên đề học tập Toán 12 - Chân trời sáng tạo không chỉ giúp bạn nắm vững kiến thức về đạo hàm mà còn có ứng dụng thực tế trong nhiều lĩnh vực khác nhau, như:
Bài 3 trang 38 Chuyên đề học tập Toán 12 - Chân trời sáng tạo là một bài tập quan trọng giúp bạn củng cố kiến thức về đạo hàm và ứng dụng của nó trong thực tế. Hy vọng rằng, với hướng dẫn chi tiết và ví dụ minh họa trong bài viết này, bạn sẽ tự tin hơn trong việc giải quyết bài toán này và đạt kết quả tốt trong các kỳ thi.