Chào mừng các em học sinh đến với lời giải chi tiết Bài 13 trang 93 sách bài tập Toán 7 tập 1 - Cánh diều. Bài viết này được giaitoan.edu.vn biên soạn nhằm hỗ trợ các em ôn tập và nắm vững kiến thức toán học.
Chúng tôi sẽ cung cấp đáp án từng câu hỏi, kèm theo phương pháp giải rõ ràng, dễ hiểu, giúp các em tự tin giải quyết các bài tập tương tự. Hãy cùng bắt đầu nhé!
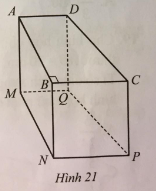
Cho hình lăng trụ đứng tứ giác ABCD.MNPQ có đáy là hình thang vuông ABCD vuông tại B (AD song song với BC) với
Đề bài
Cho hình lăng trụ đứng tứ giác ABCD.MNPQ có đáy là hình thang vuông ABCD vuông tại B (AD song song với BC) với \(AB = 20{\rm{ cm}}\), \(AD = 11{\rm{ cm}}\), \(BC = 15{\rm{ cm}}\) (Hình 21).
a) Tính tỉ số giữa thể tích của hình lăng trụ đứng tam giác ABC.MNP và thể tích của hình lăng trụ đứng tứ giác ABCD.MNPQ.
b) Tính tỉ số phần trăm giữa thể tích của hình lăng trụ đứng tam giác ABD.MNQ và thể tích của hình lăng trụ đứng tam giác BCD.NPQ.
c) So sánh thể tích của hai hình lăng trụ đứng tam giác ABD.MNQ và ACD.MPQ.
Phương pháp giải - Xem chi tiết
a) Để tính tỉ số giữa thể tích của hình lăng trụ đứng tam giác ABC.MNP và thể tích của hình lăng trụ đứng tứ giác ABCD.MNPQ, ta cần tính diện tích hai đáy tương ứng với hai hình.
b) Để tính tỉ số phần trăm giữa thể tích của hình lăng trụ đứng tam giác ABD.MNQ và thể tích của hình lăng trụ đứng tam giác BCD.NPQ, ta cần tính diện tích hai đáy tương ứng với hai hình rồi nhân với 100%.
c) Muốn so sánh thể tích của hai hình lăng trụ, ta so sánh diện tích và chiều cao tương ứng của hai hình với nhau.
Lời giải chi tiết
a) Ta có:
\({S_{ABC}} = \dfrac{{20{\rm{ }}.{\rm{ }}15}}{2} = 150{\rm{ (c}}{{\rm{m}}^2});\\{S_{ABCD}} = \dfrac{{(11 + 15){\rm{ }}.{\rm{ }}20}}{2} = 260{\rm{ (c}}{{\rm{m}}^2}).\)
Tỉ số giữa thể tích của hình lăng trụ đứng tam giác ABC.MNP và thể tích của hình lăng trụ đứng tứ giác ABCD.MNPQ là:
\(\dfrac{{{V_{ABC.MNP}}}}{{{V_{ABCD.MNPQ}}}} = \dfrac{{{S_{ABC}}{\rm{ }}.{\rm{ }}BN}}{{{S_{ABCD}}{\rm{ }}.{\rm{ }}BN}} \\= \dfrac{{{S_{ABC}}}}{{{S_{ABCD}}}} = \dfrac{{150}}{{260}} = \dfrac{{15}}{{26}}.\)
b) Ta có:
\({S_{ABD}} = \dfrac{{20{\rm{ }}.{\rm{ }}11}}{2} = 110{\rm{ (c}}{{\rm{m}}^2});\\{S_{BCD}} = \dfrac{{15{\rm{ }}.{\rm{ }}20}}{2} = 150{\rm{ (c}}{{\rm{m}}^2}).\)
Tỉ số phần trăm giữa thể tích của hình lăng trụ đứng tam giác ABD.MNQ và thể tích của hình lăng trụ đứng tam giác BCD.NPQ là:
\(\dfrac{{{V_{ABD.MNQ}}{\rm{ }}.{\rm{ }}100\% }}{{{V_{BCD.NPQ}}}} = \dfrac{{{S_{ABD}}{\rm{ }}.{\rm{ }}BN{\rm{ }}.{\rm{ }}100\% }}{{{S_{BCD}}{\rm{ }}.{\rm{ }}BN}} \\ = \dfrac{{{S_{ABD}}{\rm{ }}.{\rm{ }}100\% }}{{{S_{BCD}}}} = \dfrac{{110{\rm{ }}.{\rm{ }}100\% }}{{150}} = 73,(3)\% .\)
c) Ta có:
\({S_{ABC}} = 150{\rm{ (c}}{{\rm{m}}^2});\\{S_{ACD}} = {S_{ABCD}} - {S_{ABC}} = 260 - 150 = 110{\rm{ (c}}{{\rm{m}}^2}).\)
\({S_{ABD}} = 110{\rm{ (c}}{{\rm{m}}^2})\).
Suy ra:
\(\begin{array}{l}{S_{ACD}} = {S_{ABD}}\\ \Rightarrow {S_{ACD}}{\rm{ }}.{\rm{ }}BN = {S_{ABD}}{\rm{ }}.{\rm{ }}BN\\ \Rightarrow {V_{ABD.MNQ}} = {V_{ACD.MPQ}}\end{array}\)
Vậy thể tích của hai hình lăng trụ đứng tam giác ABD.MNQ và ACD.MPQ bằng nhau.
Bài 13 trang 93 sách bài tập Toán 7 tập 1 - Cánh diều thuộc chương trình học Toán 7, tập trung vào việc ôn tập và củng cố các kiến thức về biểu thức đại số, các phép toán với số hữu tỉ, và các tính chất của phép cộng, phép trừ, phép nhân, phép chia.
Bài 13 bao gồm các dạng bài tập sau:
Ví dụ: Tính giá trị của biểu thức 3x + 2y khi x = 2 và y = -1.
Giải:
Thay x = 2 và y = -1 vào biểu thức, ta được:
3x + 2y = 3 * 2 + 2 * (-1) = 6 - 2 = 4
Vậy giá trị của biểu thức là 4.
Ví dụ: Rút gọn biểu thức 5x - 3x + 2x.
Giải:
5x - 3x + 2x = (5 - 3 + 2)x = 4x
Vậy biểu thức được rút gọn là 4x.
Ví dụ: Một cửa hàng có x sản phẩm. Sau khi bán được 1/3 số sản phẩm, cửa hàng còn lại bao nhiêu sản phẩm?
Giải:
Số sản phẩm đã bán là x/3.
Số sản phẩm còn lại là x - x/3 = 2x/3.
Vậy cửa hàng còn lại 2x/3 sản phẩm.
Ngoài sách bài tập, các em có thể tham khảo thêm các tài liệu sau:
Hy vọng với lời giải chi tiết và hướng dẫn giải bài tập trong bài viết này, các em sẽ tự tin hơn trong việc học Toán 7. Chúc các em học tốt và đạt kết quả cao!