Chào mừng các em học sinh đến với lời giải chi tiết Bài 2 trang 103 sách bài tập Toán 7 tập 1 - Cánh diều. Bài viết này sẽ cung cấp đáp án, hướng dẫn giải bài tập một cách dễ hiểu, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán. Hãy cùng chúng tôi khám phá lời giải chi tiết ngay sau đây!
Cho các cặp tia Oa và Ob, Oc và Od là các cặp tia đối nhau. Tìm số đo mỗi góc aOc, bOc, bOd, aOd trong mỗi trường hợp sau:
Đề bài
Cho các cặp tia Oa và Ob, Oc và Od là các cặp tia đối nhau. Tìm số đo mỗi góc aOc, bOc, bOd, aOd trong mỗi trường hợp sau:
a) \(\widehat {aOc} = 75^\circ \); b) \(\widehat {aOc} + \widehat {bOd} = 140^\circ \);
c) \(\widehat {aOc} + \widehat {bOd} = \widehat {bOc} + \widehat {aOd}\); d) \(\widehat {bOc} - \widehat {aOc} = 10^\circ \);
e) \(\widehat {bOc} = 2\widehat {aOc}\).
Phương pháp giải - Xem chi tiết
Ta tìm số đo mỗi góc dựa vào những góc đã biết: Hai góc đối đỉnh có số đo góc bằng nhau, hai góc kề bù có tổng số đo góc bằng 180°.
Lời giải chi tiết
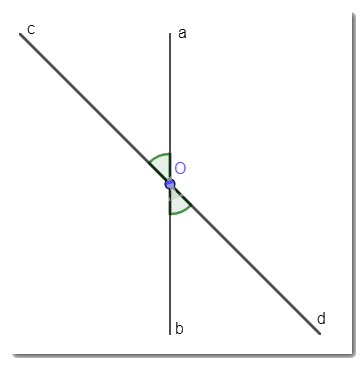
a) \(\widehat {aOc} = \widehat {bOd} = 75^\circ \) (đối đỉnh); \(\widehat {bOc} = \widehat {aOd} = 180^\circ - 75^\circ = 105^\circ \) (hai góc aOc và bOd bù nhau).
b) \(\widehat {aOc} + \widehat {bOd} = 140^\circ \to \widehat {aOc} = \widehat {bOd} = 140^\circ :2 = 70^\circ \); \(\widehat {bOc} = \widehat {aOd} = 180^\circ - 70^\circ = 110^\circ \).
c)
\(\begin{array}{l}\widehat {aOc} + \widehat {bOd} = \widehat {bOc} + \widehat {aOd} \to 2\widehat {aOc} = 2\widehat {bOc}\\ \to \widehat {aOc} = \widehat {bOd} = 180^\circ :2^\circ = 90^\circ \\ \to \widehat {aOc} = \widehat {bOd} = \widehat {bOc} = \widehat {aOd} = 90\end{array}\);
d)
\(\begin{array}{l}\left\{ \begin{array}{l}\widehat {bOc} + \widehat {aOc} = 180^\circ \\\widehat {bOc} - \widehat {aOc} = 10^\circ \end{array} \right.\\ \to \left\{ \begin{array}{l}\widehat {bOc} = \widehat {aOd} = 95^\circ \\\widehat {aOc} = \widehat {bOd} = 85^\circ \end{array} \right.\end{array}\);
e)
\(\begin{array}{l}\left\{ \begin{array}{l}\widehat {bOc} + \widehat {aOc} = 180^\circ \\\widehat {bOc} = 2\widehat {aOc}\end{array} \right.\\ \to 3\widehat {aOc} = 180^\circ \to \widehat {aOc} = \widehat {bOd} = 60^\circ \\ \to \widehat {bOc} = \widehat {aOd} = 120^\circ \end{array}\).
Bài 2 trang 103 sách bài tập Toán 7 tập 1 - Cánh diều thuộc chương trình học Toán 7, tập trung vào việc vận dụng các kiến thức về số hữu tỉ, phép cộng, trừ, nhân, chia số hữu tỉ để giải quyết các bài toán thực tế. Bài tập này yêu cầu học sinh phải hiểu rõ các quy tắc, tính chất của các phép toán và khả năng áp dụng linh hoạt vào các tình huống khác nhau.
Bài 2 bao gồm các câu hỏi nhỏ, yêu cầu học sinh thực hiện các phép tính với số hữu tỉ, so sánh số hữu tỉ và tìm số hữu tỉ thích hợp để điền vào chỗ trống. Để giải quyết bài tập này một cách hiệu quả, học sinh cần:
Câu a yêu cầu thực hiện phép cộng hai số hữu tỉ. Để giải quyết câu này, ta cần quy đồng mẫu số của hai phân số (nếu cần) và cộng tử số lại với nhau, giữ nguyên mẫu số. Ví dụ:
Nếu đề bài là: 1/2 + 1/3, ta quy đồng mẫu số thành 3/6 + 2/6 = 5/6
Câu b yêu cầu thực hiện phép trừ hai số hữu tỉ. Tương tự như phép cộng, ta cần quy đồng mẫu số (nếu cần) và trừ tử số, giữ nguyên mẫu số. Ví dụ:
Nếu đề bài là: 3/4 - 1/2, ta quy đồng mẫu số thành 3/4 - 2/4 = 1/4
Câu c yêu cầu thực hiện phép nhân hai số hữu tỉ. Để giải quyết câu này, ta nhân tử số với tử số, mẫu số với mẫu số. Ví dụ:
Nếu đề bài là: 2/3 * 1/4, ta thực hiện phép nhân: 2 * 1 / 3 * 4 = 2/12 = 1/6
Câu d yêu cầu thực hiện phép chia hai số hữu tỉ. Để giải quyết câu này, ta nhân số bị chia với nghịch đảo của số chia. Ví dụ:
Nếu đề bài là: 1/2 : 1/3, ta thực hiện phép chia: 1/2 * 3/1 = 3/2
Trong quá trình giải Bài 2, học sinh cần lưu ý một số điểm sau:
Để củng cố kiến thức và rèn luyện kỹ năng, học sinh có thể tự giải thêm các bài tập tương tự sau:
Bài 2 trang 103 sách bài tập Toán 7 tập 1 - Cánh diều là một bài tập quan trọng giúp học sinh củng cố kiến thức về số hữu tỉ và các phép toán với số hữu tỉ. Hy vọng với lời giải chi tiết và hướng dẫn cụ thể trên đây, các em sẽ tự tin hơn trong quá trình học tập và đạt kết quả tốt nhất.