Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho Bài 37 trang 81 sách bài tập Toán 7 - Cánh diều. Chúng tôi hiểu rằng việc giải bài tập có thể gặp nhiều khó khăn, đặc biệt là với những em mới bắt đầu làm quen với chương trình Toán 7.
Với đội ngũ giáo viên giàu kinh nghiệm, chúng tôi đã biên soạn lời giải Bài 37 trang 81 một cách cẩn thận, đảm bảo tính chính xác và dễ tiếp thu.
Nêu thêm một điều kiện để hai tam giác trong mỗi hình 31a, 31b, 31c, 31d là hai tam giác bằng nhau theo trường hợp góc – cạnh – góc.
Đề bài
Nêu thêm một điều kiện để hai tam giác trong mỗi hình 31a, 31b, 31c, 31d là hai tam giác bằng nhau theo trường hợp góc – cạnh – góc.
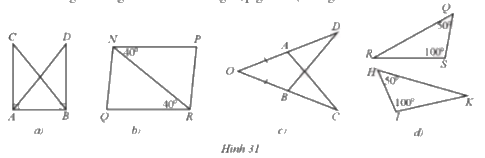
a) ∆CAB = ∆DBA (Hình 31a).
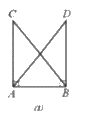
b) ∆NRQ = ∆RNP (Hình 31b).
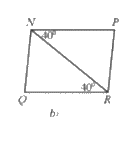
c) ∆OAC = ∆OBD (Hình 31c).
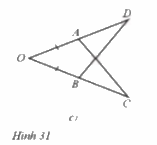
d) ∆SRQ = ∆IKH (Hình 31d).
Phương pháp giải - Xem chi tiết
Quan sát các hình để thêm các điều biện bằng nhau của tam giác theo trường hợp goc – cạnh – góc
Lời giải chi tiết
a) Hình a
Để ∆CAB = ∆DBA theo trường hợp góc – cạnh – góc thì một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia.
Mà hai tam giác trên có cạnh AB là cạnh chung và \(\widehat {CAB} = \widehat {DBA}\left( { = 90^\circ } \right)\).
Mặt khác, trong ∆CAB thì cạnh AB có hai góc kề là \(\widehat {CAB}\) và \(\widehat {ABC}\);
Trong ∆DBA thì cạnh AB có hai góc kề là \(\widehat {DBA}\) và \(\widehat {BAD}\) .
Do đó điều kiện còn lại là điều kiện về góc, đó là \(\widehat {ABC} = \widehat {BAD}\)
Vậy Hình 31a cần thêm điều kiện \(\widehat {ABC} = \widehat {BAD}\) .
b) Hình b
Để ∆NRQ = ∆RNP theo trường hợp góc – cạnh – góc thì một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia.
Mà hai tam giác trên có cạnh NR là cạnh chung và \(\widehat {PN{\rm{R}}} = \widehat {{\rm{QRN}}}\left( { = 40^\circ } \right)\).
Mặt khác, trong ∆NRQ, cạnh NR có hai góc kề là \(\widehat {PNR}\) và \(\widehat {PRN}\) ;
Trong ∆RNP, cạnh NR có hai góc kề là \(\widehat {QRN}\) và \(\widehat {QNR}\)
Do đó điều kiện còn lại là điều kiện về góc, đó là \(\widehat {PRN} = \widehat {QNR}.\)
Vậy Hình 31b cần thêm điều kiện \(\widehat {PRN} = \widehat {QNR}.\).
c) Hình c
Để ∆OAC = ∆OBD theo trường hợp góc – cạnh – góc thì một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia.
Mà hai tam giác trên có OA = OB và \(\hat O\) là góc chung.
Mặt khác, trong ∆OAC, cạnh OA có hai góc kề là \(\hat O\) và \(\widehat {OAC}\);
Trong ∆OBD, cạnh OB có hai góc kề là \(\hat O\) và \(\widehat {OBD}\) .
Do đó điều kiện còn lại là điều kiện về góc, đó là \(\widehat {OAC} = \widehat {OBD}\).
Vậy Hình 31c cần thêm điều kiện \(\widehat {OAC} = \widehat {OBD}\).
d) Hình d
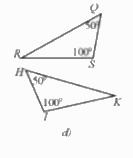
Để ∆SRQ = ∆IKH theo trường hợp góc – cạnh – góc thì một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia.
Mà hai tam giác này có \(\hat Q = \hat H\left( { = 50^\circ } \right)\) và \(\hat S = \hat I\left( { = 100^\circ } \right)\)
Mặt khác, trong ∆SRQ, \(\hat Q\) và \(\hat S\) là hai góc kề của cạnh QS;
Trong ∆IKH, \(\hat H\) và \(\hat I\) là hai góc kề của cạnh HI.
Do đó điều kiện còn lại là điều kiện về cạnh, đó là QS = HI.
Vậy Hình 31d cần thêm điều kiện QS = HI.
Bài 37 trang 81 sách bài tập Toán 7 - Cánh diều thuộc chương trình học về các góc và mối quan hệ giữa các góc tạo bởi một đường thẳng cắt hai đường thẳng song song. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức về góc so le trong, góc đồng vị, góc trong cùng phía để chứng minh tính chất của các góc hoặc giải các bài toán liên quan đến góc.
Bài 37 thường bao gồm các dạng bài tập sau:
Để xác định các cặp góc so le trong, đồng vị, trong cùng phía, học sinh cần nắm vững định nghĩa của từng loại góc. Ví dụ, góc so le trong là hai góc nằm bên trong hai đường thẳng song song và ở hai phía của đường thẳng cắt.
Khi gặp bài toán, hãy vẽ hình minh họa để dễ dàng quan sát và xác định các góc. Sử dụng ký hiệu để đánh dấu các góc cần xét.
Để chứng minh hai đường thẳng song song, học sinh có thể sử dụng các tiêu chuẩn sau:
Khi chứng minh, cần nêu rõ tiêu chuẩn được sử dụng và giải thích tại sao tiêu chuẩn đó được áp dụng.
Khi tính số đo của các góc, học sinh cần vận dụng các tính chất của góc đã học, chẳng hạn như:
Sử dụng các phương trình để biểu diễn mối quan hệ giữa các góc và giải phương trình để tìm ra số đo của các góc cần tính.
Ví dụ: Cho hình vẽ, biết góc A1 = 60 độ. Tính số đo của các góc A2, B1, B2.
Giải:
Ngoài sách bài tập Toán 7 - Cánh diều, học sinh có thể tham khảo thêm các tài liệu sau để nắm vững kiến thức về góc và đường thẳng song song:
Bài 37 trang 81 sách bài tập Toán 7 - Cánh diều là một bài tập quan trọng giúp học sinh củng cố kiến thức về góc và đường thẳng song song. Bằng cách nắm vững các định nghĩa, tính chất và phương pháp giải, học sinh có thể tự tin giải quyết các bài toán tương tự.