Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho Bài 70 trang 89 sách bài tập Toán 7 - Cánh diều. Chúng tôi hiểu rằng việc giải bài tập có thể gặp nhiều khó khăn, đặc biệt là với những em mới làm quen với chương trình Toán 7.
Bài viết này sẽ giúp bạn nắm vững kiến thức, phương pháp giải và tự tin hơn trong quá trình học tập.
Cho tam giác ABC cân tại A có hai trung tuyến BM và CN cắt nhau tại G. Chứng minh: a) BM = CN;
Đề bài
Cho tam giác ABC cân tại A có hai trung tuyến BM và CN cắt nhau tại G. Chứng minh:
a) BM = CN;
b) Tam giác GBC là tam giác cân;
c) AG vuông góc với BC.
Phương pháp giải - Xem chi tiết
- Sử dụng tính chất ba đường trung tuyến để chứng minh: \(\Delta ABM = \Delta ACN(c - g - c)\) suy ra BM = CN.
- Chứng minh: \(\widehat {GBC} = \widehat {GCB}\) suy ra tam giác GBC cân tại G.
- Chứng minh: AG là đường trung trực của đoạn thẳng BC.
Suy ra: AG vuông góc với BC.
Lời giải chi tiết
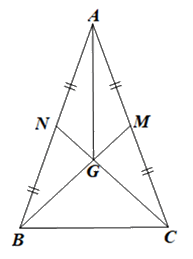
a) Vì tam giác ABC cân tại A nên AB = AC, \(\widehat {ABC} = \widehat {ACB}\).
Vì BM, CN là đường trung tuyến của tam giác ABC nên M, N lần lượt là trung điểm của AC và AB.
Do đó AM = MC, AN = NB.
Mà AB = AC
Suy ra AM = MC = AN = NB.
Xét ∆ABM và ∆ACN có:
AB = AC (chứng minh trên),
\(\widehat {BAC}\) là góc chung,
AM = AN (chứng minh trên)
Do đó ∆ABM = ∆ACN (c.g.c).
Suy ra BM = CN (hai cạnh tương ứng).
Vậy BM = CN.
b) Do ∆AMB = ∆ANC (câu a) suy ra \(\widehat {ABM} = \widehat {ACN}\) (hai góc tương ứng).
Ta có \(\widehat {ACB} = \widehat {ACN} + \widehat {NCB}\), .
Mà \(\widehat {ABC} = \widehat {ACB}\) và \(\widehat {ABM} = \widehat {ACN}\).
Nên \(\widehat {MBC} = \widehat {NCB}\) hay \(\widehat {GBC} = \widehat {GCB}\).
Suy ra tam giác GBC cân tại G.
Vậy tam giác GBC cân tại G
c) Ta có AB = AC nên A nằm trên đường trung trực của đoạn thẳng BC.
Theo câu b tam giác GBC cân tại G nên GB = GC (hai cạnh bên).
Do đó G nằm trên trung trực của đoạn thẳng BC.
Suy ra AG là đường trung trực của đoạn thẳng BC nên AG vuông góc với BC tại trung điểm của BC.
Vậy AG vuông góc với BC.
Bài 70 trang 89 sách bài tập Toán 7 - Cánh diều thuộc chương trình học về các phép biến đổi đơn giản với đa thức. Bài tập này yêu cầu học sinh vận dụng các kiến thức đã học để thực hiện các phép cộng, trừ, nhân, chia đa thức một cách chính xác.
Bài 70 bao gồm các câu hỏi và bài tập khác nhau, tập trung vào việc:
Đề bài: Thực hiện phép tính: (3x + 2y) + (x - y)
Lời giải:
(3x + 2y) + (x - y) = 3x + 2y + x - y = (3x + x) + (2y - y) = 4x + y
Đề bài: Thực hiện phép tính: (5a - 3b) - (2a + b)
Lời giải:
(5a - 3b) - (2a + b) = 5a - 3b - 2a - b = (5a - 2a) + (-3b - b) = 3a - 4b
Đề bài: Thực hiện phép tính: 2x(x - 3)
Lời giải:
2x(x - 3) = 2x * x - 2x * 3 = 2x2 - 6x
Đề bài: Thực hiện phép tính: (x + 2)(x - 1)
Lời giải:
(x + 2)(x - 1) = x(x - 1) + 2(x - 1) = x2 - x + 2x - 2 = x2 + x - 2
Trong Bài 70, học sinh có thể gặp các dạng bài tập sau:
Để giải bài tập Bài 70 một cách hiệu quả, bạn nên:
Kiến thức về các phép toán với đa thức có ứng dụng rộng rãi trong nhiều lĩnh vực của Toán học, đặc biệt là trong việc giải phương trình, bất phương trình và các bài toán về hàm số.
Hy vọng rằng với hướng dẫn chi tiết này, bạn đã có thể tự tin giải Bài 70 trang 89 sách bài tập Toán 7 - Cánh diều. Chúc bạn học tập tốt và đạt kết quả cao!