Bài học này giúp các em học sinh ôn tập lại kiến thức về các hình phẳng đã học như hình vuông, hình chữ nhật, hình tam giác, hình bình hành và hình thang. Thông qua việc giải các bài tập trong vở bài tập, các em sẽ củng cố kỹ năng tính diện tích và chu vi của các hình này.
Giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu cho từng bài tập, giúp các em tự học tại nhà hiệu quả. Ngoài ra, chúng tôi còn có nhiều bài giảng và tài liệu hỗ trợ học tập khác.
Tính diện tích mỗi hình tam giác dưới đây.
Giải Bài 3 trang 121 VBT Toán 5 tập 1 – Kết nối tri thức với cuộc sống
Hoàn thành bảng sau.
Bán kính hình tròn | 2 cm | 10 cm | 3 dm | 1 m |
Chu vi hình tròn | ||||
Diện tích hình tròn |
Phương pháp giải:
Chu vi hình tròn = đường kính × 3,14 = bán kính × 2 × 3,14
Diện tích hình tròn = bán kính × bán kính × 3,14
Lời giải chi tiết:
Bán kính hình tròn | 2 cm | 10 cm | 3 dm | 1 m |
Chu vi hình tròn | 12,56 cm | 62,8 cm | 18,84 dm | 6,28 m |
Diện tích hình tròn | 12,56 cm² | 314 cm² | 28,26 dm² | 3,14 dm² |
Giải Bài 4 trang 121 VBT Toán 5 tập 1 – Kết nối tri thức với cuộc sống
Viết số thập phân thích hợp vào chỗ chấm.
Rô-bốt vẽ 1 hình tròn lớn và 2 hình tròn nhỏ rồi tô màu như hình vẽ bên. Hình tròn lớn có bán kính 10 cm và mỗi hình tròn nhỏ có bán kính 5 cm. Diện tích phần tô màu là ……………….. cm².
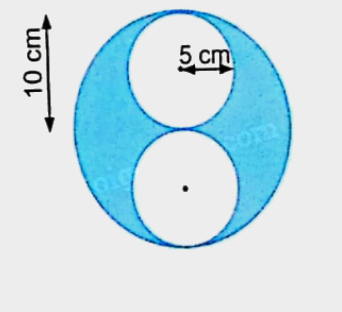
Phương pháp giải:
1. Tìm diện tích hình tròn lớn = bán kính x bán kính x 3,14
2. Tìm diện tích hình tròn nhỏ = bán kính x bán kính x 3,14
3. Diện tích phần tô màu = Diện tích hình tròn lớn – 2 × diện tích hình tròn nhỏ
Lời giải chi tiết:
Diện tích hình tròn lớn là 10 × 10 × 3,14 = 314 (cm²)
Diện tích hình tròn nhỏ là 5 x 5 x 3,14 = 78,5 (cm²)
Diện tích phần tô màu là 314 - 78,5 x 2 = 157 (cm²)
Giải Bài 2 trang 121 VBT Toán 5 tập 1 – Kết nối tri thức với cuộc sống
Tính diện tích mỗi hình thang dưới đây.
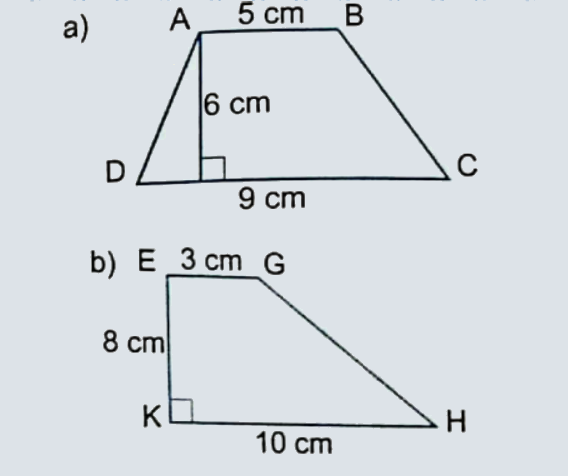
Phương pháp giải:
Diện tích hình thang: S = $\frac{{(a + b) \times h}}{2}$
Trong đó:
+ S: diện tích
+ a, b: độ dài các đáy
+ h: chiều cao
Lời giải chi tiết:
a)
Diện tích hình thang ABCD là:
$$\frac{{(9 + 5) \times 6}}{2} = 42 (cm²)$$
Đáp số: 42 cm²
b)
Diện tích hình thang EGHK là:
$$\frac{{(10 + 3) \times 8}}{2} = 52 (cm²)$$
Đáp số: 52 cm²
Giải Bài 1 trang 120 VBT Toán 5 tập 1 – Kết nối tri thức với cuộc sống
Tính diện tích mỗi hình tam giác dưới đây.
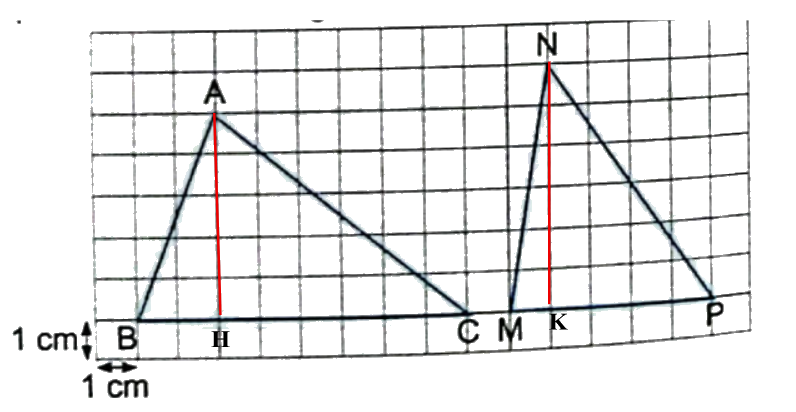
Phương pháp giải:
Trong tam giác ABC, độ dài cạnh đáy BC là: 8 cm
Kẻ đường cao AH từ đỉnh A xuống, ta được đường cao AH có độ dài là: 5 cm
Trong tam giác NMP, độ dài cạnh đáy MP là: 5 cm
Kẻ đường cao NK từ đỉnh N xuống, ta được đường cao NK có độ dài là: 6 cm
Diện tích tam giác = $\frac{1}{{2}}$ x đáy × chiều cao
Lời giải chi tiết:
Diện tích tam giác ABC là:
\(\frac{{8 \times 5}}{2} = 20\) (cm²)
Diện tích tam giác NMP là:
$\frac{{5 \times 6}}{2} = 15$ (cm²)
Đáp số: Tam giác ABC: 20 cm²
Tam giác NMP: 15 cm²
Giải Bài 1 trang 120 VBT Toán 5 tập 1 – Kết nối tri thức với cuộc sống
Tính diện tích mỗi hình tam giác dưới đây.
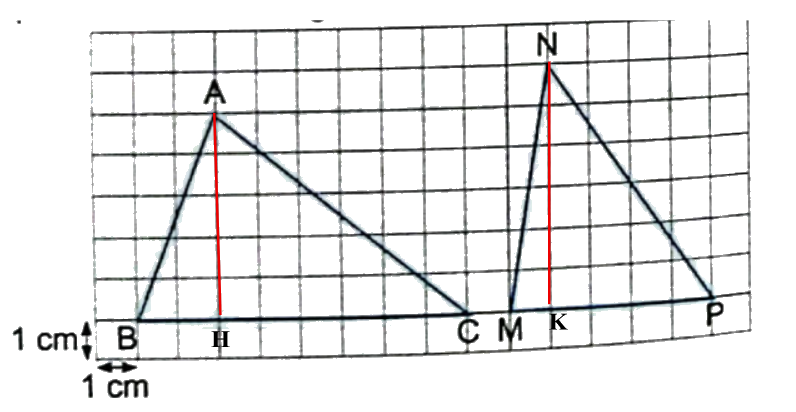
Phương pháp giải:
Trong tam giác ABC, độ dài cạnh đáy BC là: 8 cm
Kẻ đường cao AH từ đỉnh A xuống, ta được đường cao AH có độ dài là: 5 cm
Trong tam giác NMP, độ dài cạnh đáy MP là: 5 cm
Kẻ đường cao NK từ đỉnh N xuống, ta được đường cao NK có độ dài là: 6 cm
Diện tích tam giác = $\frac{1}{{2}}$ x đáy × chiều cao
Lời giải chi tiết:
Diện tích tam giác ABC là:
\(\frac{{8 \times 5}}{2} = 20\) (cm²)
Diện tích tam giác NMP là:
$\frac{{5 \times 6}}{2} = 15$ (cm²)
Đáp số: Tam giác ABC: 20 cm²
Tam giác NMP: 15 cm²
Giải Bài 2 trang 121 VBT Toán 5 tập 1 – Kết nối tri thức với cuộc sống
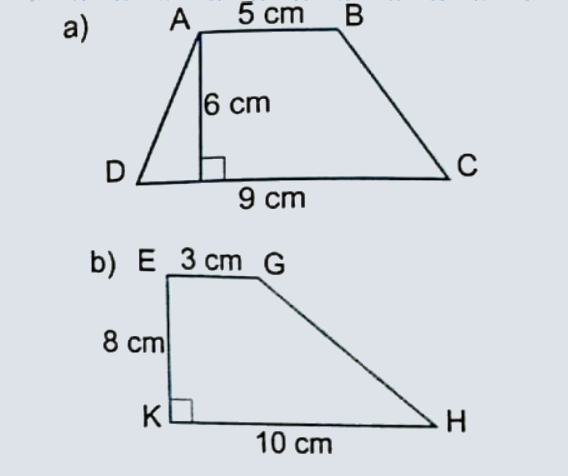
Tính diện tích mỗi hình thang dưới đây.
Phương pháp giải:
Diện tích hình thang: S = $\frac{{(a + b) \times h}}{2}$
Trong đó:
+ S: diện tích
+ a, b: độ dài các đáy
+ h: chiều cao
Lời giải chi tiết:
a)
Diện tích hình thang ABCD là:
$$\frac{{(9 + 5) \times 6}}{2} = 42 (cm²)$$
Đáp số: 42 cm²
b)
Diện tích hình thang EGHK là:
$$\frac{{(10 + 3) \times 8}}{2} = 52 (cm²)$$
Đáp số: 52 cm²
Giải Bài 3 trang 121 VBT Toán 5 tập 1 – Kết nối tri thức với cuộc sống
Hoàn thành bảng sau.
Bán kính hình tròn | 2 cm | 10 cm | 3 dm | 1 m |
Chu vi hình tròn | ||||
Diện tích hình tròn |
Phương pháp giải:
Chu vi hình tròn = đường kính × 3,14 = bán kính × 2 × 3,14
Diện tích hình tròn = bán kính × bán kính × 3,14
Lời giải chi tiết:
Bán kính hình tròn | 2 cm | 10 cm | 3 dm | 1 m |
Chu vi hình tròn | 12,56 cm | 62,8 cm | 18,84 dm | 6,28 m |
Diện tích hình tròn | 12,56 cm² | 314 cm² | 28,26 dm² | 3,14 dm² |
Giải Bài 4 trang 121 VBT Toán 5 tập 1 – Kết nối tri thức với cuộc sống
Viết số thập phân thích hợp vào chỗ chấm.
Rô-bốt vẽ 1 hình tròn lớn và 2 hình tròn nhỏ rồi tô màu như hình vẽ bên. Hình tròn lớn có bán kính 10 cm và mỗi hình tròn nhỏ có bán kính 5 cm. Diện tích phần tô màu là ……………….. cm².
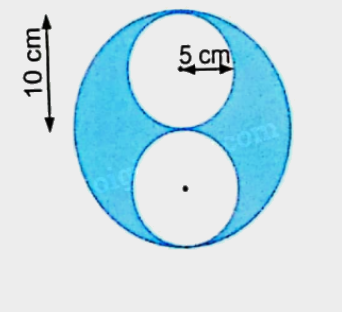
Phương pháp giải:
1. Tìm diện tích hình tròn lớn = bán kính x bán kính x 3,14
2. Tìm diện tích hình tròn nhỏ = bán kính x bán kính x 3,14
3. Diện tích phần tô màu = Diện tích hình tròn lớn – 2 × diện tích hình tròn nhỏ
Lời giải chi tiết:
Diện tích hình tròn lớn là 10 × 10 × 3,14 = 314 (cm²)
Diện tích hình tròn nhỏ là 5 x 5 x 3,14 = 78,5 (cm²)
Diện tích phần tô màu là 314 - 78,5 x 2 = 157 (cm²)
Bài 32 trong Vở bài tập Toán 5 - Kết nối tri thức tập trung vào việc ôn tập các kiến thức quan trọng về các hình phẳng. Đây là một bước quan trọng để học sinh nắm vững nền tảng toán học, chuẩn bị cho các bài học tiếp theo và các kỳ thi.
Trước khi đi vào giải bài tập, chúng ta cùng ôn lại một số kiến thức cơ bản về các hình phẳng:
Dưới đây là lời giải chi tiết cho các bài tập trong Vở bài tập Toán 5 - Kết nối tri thức trang 120:
Để hiểu sâu hơn về các hình phẳng và rèn luyện kỹ năng giải bài tập, các em có thể tham khảo thêm các bài tập sau:
Ví dụ về bài tập mở rộng: Một mảnh đất hình chữ nhật có chiều dài 20m và chiều rộng 15m. Tính diện tích mảnh đất đó.
Lời giải: Diện tích mảnh đất là: 20m x 15m = 300m2
Khi giải các bài tập về hình phẳng, các em cần lưu ý những điều sau:
Hy vọng với những hướng dẫn chi tiết này, các em sẽ tự tin hơn khi giải các bài tập về hình phẳng trong Vở bài tập Toán 5 - Kết nối tri thức. Chúc các em học tốt!
Bảng tổng hợp công thức tính diện tích và chu vi:
| Hình | Diện tích | Chu vi |
|---|---|---|
| Hình vuông | Cạnh x Cạnh | Cạnh x 4 |
| Hình chữ nhật | Chiều dài x Chiều rộng | (Chiều dài + Chiều rộng) x 2 |
| Hình tam giác | (Đáy x Chiều cao) / 2 | Tổng độ dài ba cạnh |
| Hình bình hành | Đáy x Chiều cao | (Đáy + Cạnh bên) x 2 |
| Hình thang | (Tổng hai đáy x Chiều cao) / 2 | Tổng độ dài bốn cạnh |