Chào mừng các em học sinh đến với bài giải bài 5 trong chương trình ôn tập các phép tính với phân số lớp 5. Bài học này nằm trong tiết 3 của chương trình và được trình bày trong vở bài tập Toán 5 - Kết nối tri thức.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải các bài tập về phân số.
Điền Đ, S
Giải Bài 2 trang 18 VBT Toán 5 tập 1 – Kết nối tri thức với cuộc sống
Tính giá trị của biểu thức
a) \(\frac{8}{{15}} \times \left( {\frac{1}{8} + \frac{3}{4}} \right) = ... \)
b) \(\frac{{28}}{{24}} - \frac{4}{6}:2 = ... \)
Phương pháp giải:
- Nếu biểu thức có phép tính cộng, trừ và phép tính nhân, chia thì ta thực hiện phép tính nhân, chia trước; thực hiện phép tính cộng, trừ sau.
- Nếu biểu thức chứa dấu ngoặc thì ta thực hiện trong ngoặc trước.
Lời giải chi tiết:
a) \(\frac{8}{{15}} \times \left( {\frac{1}{8} + \frac{3}{4}} \right) = \frac{8}{{15}} \times \frac{7}{8} = \frac{7}{{15}}\)
b) \(\frac{{28}}{{24}} - \frac{4}{6}:2 = \frac{{28}}{{24}} - \frac{1}{3} = \frac{{28}}{{24}} - \frac{8}{{24}} = \frac{{20}}{{24}} = \frac{5}{6}\)
Giải Bài 3 trang 18 VBT Toán 5 tập 1 – Kết nối tri thức với cuộc sống
Hưởng ứng phong trào trồng cây xanh, lớp 5A trồng được 72 cây, lớp 5B trồng được số cây bằng \(\frac{8}{9}\)số cây của lớp 5A. Hỏi cả lớp 5A và lớp 5B trồng được bao nhiêu cây?
Phương pháp giải:
Số cây lớp 5B trồng được = số cây lớp 5A trồng được
Số cây lớp 5A và 5B trồng = số cây lớp 5A trồng được + số cây lớp 5B trồng
Lời giải chi tiết:
Bài giải
Lớp 5B trồng được số cây là:
\(72 \times \frac{8}{9} = 64\)(cây)
Cả lớp 5A và lớp 5B trồng được số cây là:
72 + 64 = 136 (cây)
Đáp số: 136 cây
Giải Bài 4 trang 19 VBT Toán 5 tập 1 – Kết nối tri thức với cuộc sống
Tính bằng cách thuận tiện
a) \(\frac{5}{{13}} \times \frac{3}{8} + \frac{8}{{13}} \times \frac{3}{8} = ...\)
b) \(\frac{7}{8} \times \frac{{11}}{6} + \frac{{11}}{6} \times \frac{7}{8} = ... \)
Phương pháp giải:
Áp dụng nhân một số với một tổng để tính giá trị biểu thức.
a b + a c = a (b + c)
Lời giải chi tiết:
a) \(\frac{5}{{13}} \times \frac{3}{8} + \frac{8}{{13}} \times \frac{3}{8} = \frac{3}{8} \times \left( {\frac{5}{{13}} + \frac{8}{{13}}} \right) = \frac{3}{8} \times 1 = \frac{3}{8}\)
b) \(\frac{7}{8} \times \frac{{11}}{6} + \frac{{11}}{6} \times \frac{7}{8} = \frac{7}{8} \times \left( {\frac{{11}}{6} + \frac{1}{6}} \right) = \frac{7}{8} \times 2 = \frac{7}{4}\)
Giải Bài 1 trang 18 VBT Toán 5 tập 1 – Kết nối tri thức với cuộc sống
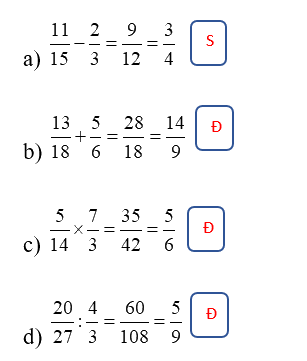
a) \(\frac{{11}}{{15}} - \frac{2}{3} = \frac{9}{{12}} = \frac{3}{4}\)
b) \(\frac{{13}}{{18}} + \frac{5}{6} = \frac{{28}}{{18}} = \frac{{14}}{9}\)
c) \(\frac{5}{{14}} \times \frac{7}{3} = \frac{{35}}{{42}} = \frac{5}{6}\)
d) \(\frac{{20}}{{27}}:\frac{4}{3} = \frac{{60}}{{108}} = \frac{5}{9}\)
Phương pháp giải:
Thực hiện các phép tính, nếu đúng ghi Đ, nếu sai ghi S.
Lời giải chi tiết:
Giải Bài 5 trang 19 VBT Toán 5 tập 1 – Kết nối tri thức với cuộc sống
Đố em!

Phương pháp giải:
Tính đoạn dây cần cắt đi bằng cách tính đoạn dây ban đầu dài hơn đoạn dây cần có bao nhiêu mét.
Tìm cách gấp dây để cắt được đoạn dây dài 1m.
Lời giải chi tiết:
\(\frac{4}{3}\)m hơn 1m số mét là:
\(\frac{4}{3} - 1 = \frac{1}{3}\)(m)
Vậy ta cần cắt đoạn dây ban đầu đi \(\frac{1}{3}\)m thì được đoạn dây dài 1m.
Để đo \(\frac{1}{3}\)m mà không dùng thước đo, ta thực hiện bằng cách gấp băng giấy thành các phần có độ dài như nhau.
\(\frac{4}{3}\)m hơn \(\frac{1}{3}\)m số mét là:
\(\frac{4}{3}:\frac{1}{3} = 4\) (lần)
Vậy ta gấp đoạn dây ban đầu thành 4 phần (mỗi phần có độ dài là\(\frac{1}{3}\)m ), ta cắt 1 phần đã gấp thì được phần còn lại là đoạn dây dài đúng bằng 1m.
Giải Bài 1 trang 18 VBT Toán 5 tập 1 – Kết nối tri thức với cuộc sống
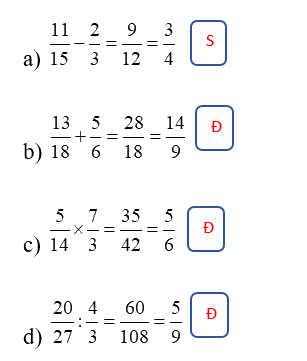
a) \(\frac{{11}}{{15}} - \frac{2}{3} = \frac{9}{{12}} = \frac{3}{4}\)
b) \(\frac{{13}}{{18}} + \frac{5}{6} = \frac{{28}}{{18}} = \frac{{14}}{9}\)
c) \(\frac{5}{{14}} \times \frac{7}{3} = \frac{{35}}{{42}} = \frac{5}{6}\)
d) \(\frac{{20}}{{27}}:\frac{4}{3} = \frac{{60}}{{108}} = \frac{5}{9}\)
Phương pháp giải:
Thực hiện các phép tính, nếu đúng ghi Đ, nếu sai ghi S.
Lời giải chi tiết:
Giải Bài 2 trang 18 VBT Toán 5 tập 1 – Kết nối tri thức với cuộc sống
Tính giá trị của biểu thức
a) \(\frac{8}{{15}} \times \left( {\frac{1}{8} + \frac{3}{4}} \right) = ... \)
b) \(\frac{{28}}{{24}} - \frac{4}{6}:2 = ... \)
Phương pháp giải:
- Nếu biểu thức có phép tính cộng, trừ và phép tính nhân, chia thì ta thực hiện phép tính nhân, chia trước; thực hiện phép tính cộng, trừ sau.
- Nếu biểu thức chứa dấu ngoặc thì ta thực hiện trong ngoặc trước.
Lời giải chi tiết:
a) \(\frac{8}{{15}} \times \left( {\frac{1}{8} + \frac{3}{4}} \right) = \frac{8}{{15}} \times \frac{7}{8} = \frac{7}{{15}}\)
b) \(\frac{{28}}{{24}} - \frac{4}{6}:2 = \frac{{28}}{{24}} - \frac{1}{3} = \frac{{28}}{{24}} - \frac{8}{{24}} = \frac{{20}}{{24}} = \frac{5}{6}\)
Giải Bài 3 trang 18 VBT Toán 5 tập 1 – Kết nối tri thức với cuộc sống
Hưởng ứng phong trào trồng cây xanh, lớp 5A trồng được 72 cây, lớp 5B trồng được số cây bằng \(\frac{8}{9}\)số cây của lớp 5A. Hỏi cả lớp 5A và lớp 5B trồng được bao nhiêu cây?
Phương pháp giải:
Số cây lớp 5B trồng được = số cây lớp 5A trồng được
Số cây lớp 5A và 5B trồng = số cây lớp 5A trồng được + số cây lớp 5B trồng
Lời giải chi tiết:
Bài giải
Lớp 5B trồng được số cây là:
\(72 \times \frac{8}{9} = 64\)(cây)
Cả lớp 5A và lớp 5B trồng được số cây là:
72 + 64 = 136 (cây)
Đáp số: 136 cây
Giải Bài 4 trang 19 VBT Toán 5 tập 1 – Kết nối tri thức với cuộc sống
Tính bằng cách thuận tiện
a) \(\frac{5}{{13}} \times \frac{3}{8} + \frac{8}{{13}} \times \frac{3}{8} = ...\)
b) \(\frac{7}{8} \times \frac{{11}}{6} + \frac{{11}}{6} \times \frac{7}{8} = ... \)
Phương pháp giải:
Áp dụng nhân một số với một tổng để tính giá trị biểu thức.
a b + a c = a (b + c)
Lời giải chi tiết:
a) \(\frac{5}{{13}} \times \frac{3}{8} + \frac{8}{{13}} \times \frac{3}{8} = \frac{3}{8} \times \left( {\frac{5}{{13}} + \frac{8}{{13}}} \right) = \frac{3}{8} \times 1 = \frac{3}{8}\)
b) \(\frac{7}{8} \times \frac{{11}}{6} + \frac{{11}}{6} \times \frac{7}{8} = \frac{7}{8} \times \left( {\frac{{11}}{6} + \frac{1}{6}} \right) = \frac{7}{8} \times 2 = \frac{7}{4}\)
Giải Bài 5 trang 19 VBT Toán 5 tập 1 – Kết nối tri thức với cuộc sống
Đố em!

Phương pháp giải:
Tính đoạn dây cần cắt đi bằng cách tính đoạn dây ban đầu dài hơn đoạn dây cần có bao nhiêu mét.
Tìm cách gấp dây để cắt được đoạn dây dài 1m.
Lời giải chi tiết:
\(\frac{4}{3}\)m hơn 1m số mét là:
\(\frac{4}{3} - 1 = \frac{1}{3}\)(m)
Vậy ta cần cắt đoạn dây ban đầu đi \(\frac{1}{3}\)m thì được đoạn dây dài 1m.
Để đo \(\frac{1}{3}\)m mà không dùng thước đo, ta thực hiện bằng cách gấp băng giấy thành các phần có độ dài như nhau.
\(\frac{4}{3}\)m hơn \(\frac{1}{3}\)m số mét là:
\(\frac{4}{3}:\frac{1}{3} = 4\) (lần)
Vậy ta gấp đoạn dây ban đầu thành 4 phần (mỗi phần có độ dài là\(\frac{1}{3}\)m ), ta cắt 1 phần đã gấp thì được phần còn lại là đoạn dây dài đúng bằng 1m.
Bài 5 trong chương trình Toán 5 - Kết nối tri thức, tiết 3, tập trung vào việc ôn tập lại các phép tính cơ bản với phân số. Đây là một phần quan trọng trong chương trình học, giúp học sinh củng cố kiến thức nền tảng để giải quyết các bài toán phức tạp hơn.
Trước khi đi vào giải bài tập, chúng ta cùng ôn lại lý thuyết về các phép tính với phân số:
Lưu ý: Để thực hiện các phép tính cộng, trừ phân số, chúng ta cần quy đồng mẫu số trước khi thực hiện phép tính.
Dưới đây là lời giải chi tiết cho từng bài tập trong bài 5:
Tương tự như bài 1, các em cần quy đồng mẫu số (nếu cần) và thực hiện phép tính. Sau khi tính được kết quả, hãy rút gọn phân số về dạng tối giản.
Giải:
Giải:
Số gạo đã dùng: 3/5 * 1/3 = 1/5 (số gạo)
Số gạo còn lại: 3/5 - 1/5 = 2/5 (số gạo)
Để củng cố kiến thức về các phép tính với phân số, các em có thể tự giải thêm các bài tập sau:
Bài 5: Ôn tập các phép tính với phân số (tiết 3) trang 18, 19 Vở bài tập Toán 5 - Kết nối tri thức là một bài học quan trọng giúp các em nắm vững kiến thức cơ bản về phân số. Việc luyện tập thường xuyên sẽ giúp các em tự tin giải quyết các bài toán liên quan đến phân số một cách hiệu quả.