Bài 75 Toán 5 thuộc chương trình ôn tập cuối năm, giúp học sinh củng cố kiến thức đã học về các phép tính với số thập phân, đo lường thời gian, diện tích hình chữ nhật và hình vuông. Bài tập trong bài ôn tập này đòi hỏi học sinh phải vận dụng linh hoạt các kiến thức đã học để giải quyết các bài toán thực tế.
Giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu cho từng bài tập trong Bài 75, giúp học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Biểu đồ dưới đây cho biết số học sinh tham gia bốn môn Cờ vua, Bóng ném, Võ dân tộc, Bơi trong Hội khoẻ Phù Đổng của một trường tiểu học.
Giải Bài 3 trang 135 VBT Toán 5 tập 1 – Kết nối tri thức với cuộc sống
Cùng xuất phát ở bến A đi đến khu du lịch B, Việt đi xe buýt thì đến nơi lúc 8 giờ 15 phút, Mai đi xe taxi đến nơi lúc 7 giờ 30 phút. Rô-bốt cho biết cùng trên quãng đường AB, thời gian đi của taxi bằng $\frac{2}{{3}}$ thời gian đi của xe buýt.
a) Tính thời gian của mỗi xe ô tô đi trên quãng đường AB.
b) Tính độ dài quãng đường AB. Biết vận tốc của xe buýt là 40 km/h.
Phương pháp giải:
a)
1. Vẽ sơ đồ: coi thời gian đi của taxi (đóng vai trò số bé) gồm 2 phần bằng nhau thì thời gian của xe buýt (đóng vai trò số lớn) gồm 3 phần bằng nhau như thế.
2. Tìm hiệu số phần bằng nhau.
3. Tìm số bé (lấy giá trị một phần nhân với số phần của số bé).
4. Tìm số lớn (lấy giá trị một phần nhân với số phần của số lớn).
b)
Quãng đường = Vận tốc x Thời gian.
Lời giải chi tiết:
a)
Thời gian đi của xe buýt dài hơn thời gian đi của taxi là:
8 giờ 15 phút - 7 giờ 30 phút = 45 phút = 0,75 (giờ)
Hiệu số phần bằng nhau là:
3 – 2 = 1 (phần)
Thời gian đi xe taxi là:
0,75 : 1 x 2 = 1,5 (giờ)
Thời gian đi xe buýt là:
1,5 + 0,75 = 2,25 (giờ)
b) Độ dài quãng đường AB là:
40 x 2,25 = 90 (km)
Đáp số: a) 1,5 giờ; 2,25 giờ
b) 90 km.
Giải Bài 2 trang 135 VBT Toán 5 tập 1 – Kết nối tri thức với cuộc sống
Viết số thích hợp vào chỗ chấm.
Một bể cá dạng hình hộp chữ nhật có chu vi đáy là 300 cm, chiều dài hơn chiều rộng 30 cm, chiều cao bể cá là 60 cm.
a) - Chiều dài đáy bể cá là .......... cm.
- Chiều rộng đáy bể cá là .......... cm.
b) Biết mực nước ở bể cá là 42 cm.
Lượng nước trong bể chiếm ........% so với lượng nước khi đầy bể.
Phương pháp giải:
a)
- Chiều dài = (Nửa chu vi đáy + Chênh lệch kích thước chiều dài và chiều rộng) : 2.
- Chiều rộng = Nửa chu vi đáy – Chiều dài.
b)
- Thể tích bể cá = Chiều dài x Chiều rộng x Chiều cao.
- Thể tích nước trong bể cá = Chiều dài x Chiều rộng x Chiều cao mực nước.
- Tỉ số phần trăm của lượng nước hiện có trong bể với lượng nước khi đầy bể = Thể tích nước trong bể cá : Thể tích bể cá x 100%.
Lời giải chi tiết:
a)
- Chiều dài đáy bể cá là (300 : 2 + 30) : 2 = 90 cm.
- Chiều rộng đáy bể cá là 300 : 2 – 90 = 60 cm.
b)
Thể tích bể cá là:
90 x 60 x 60 = 324 000 (cm3)
Thể tích nước trong bể cá là:
90 x 60 x 42 = 226 800 (cm3)
Tỉ số phần trăm của lượng nước hiện có trong bể với lượng nước khi đầy bể là:
226 800 : 324 000 = 70%
Lượng nước trong bể chiếm 70% so với lượng nước khi đầy bể.
Giải Bài 4 trang 135 VBT Toán 5 tập 1 – Kết nối tri thức với cuộc sống
Viết số thích hợp vào chỗ chấm.
Một tỉnh miền núi có diện tích khoảng 10 000 km2. Hiện tại, mật độ dân số ở tỉnh đó khoảng 80 người/km2 (nghĩa là cứ mỗi ki-lô-mét vuông có trung bình 80 người).
Nếu muốn tăng mật độ dân số của tỉnh đó lên 92 người/km2 thì:
a) Số dân của tỉnh phải tăng thêm ............... người.
b) Số dân phải tăng thêm bằng ........% số dân hiện tại.
Phương pháp giải:
a)
- Số dân của tỉnh với mật độ 80 người/km2 = Diện tích tỉnh x Mật độ dân số.
- Số dân của tỉnh với mật độ 92 người/km2 = Diện tích tỉnh x Mật độ dân số.
- Số dân của tỉnh phải tăng lên để mật độ dân số là 92 người/km2 = Số dân của tỉnh với mật độ 92 người/km2 - Số dân của tỉnh với mật độ 80 người/km2.
b) Phần trăm số dân tăng thêm so với số dân hiện tại = Số dân tăng thêm : Số dân hiện tại x 100%.
Lời giải chi tiết:
a) Số dân của tỉnh với mật độ 80 người/km2 là:
10 000 x 80 = 800 000 (người)
Số dân của tỉnh với mật độ 92 người/km2 là:
10 000 x 92 = 920 000 (người)
Muốn tăng mật độ dân số của tỉnh đó là 92 người/km2 thì số dân của tỉnh phải tăng thêm số người là:
920 000 – 800 000 = 120 000 (người)
Số dân của tỉnh phải tăng thêm 120 000 người.
b)
Số dân tăng thêm chiếm số phần trăm là:
120 000 : 800 000 x 100% = 15%
Số dân phải tăng thêm bằng 15 % số dân hiện tại.
Giải Bài 1 trang 134 VBT Toán 5 tập 1 – Kết nối tri thức với cuộc sống
Biểu đồ dưới đây cho biết số học sinh tham gia bốn môn Cờ vua, Bóng ném, Võ dân tộc, Bơi trong Hội khoẻ Phù Đổng của một trường tiểu học.
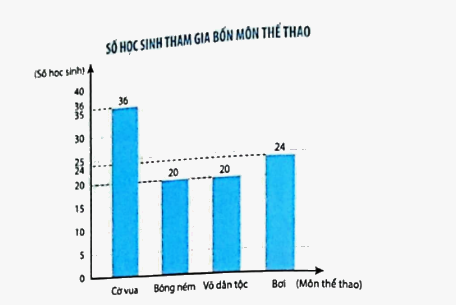
a) Hoàn thành bảng sau.
Môn | Bơi | Võ dân tộc | Bóng ném | Cờ vua |
Học sinh |
b) Tìm tỉ số phần trăm của số học sinh tham gia ở mỗi môn và tổng số học sinh tham gia.
Phương pháp giải:
a) Quan sát biểu đồ rồi trả lời câu hỏi
b) Tỉ số phần trăm của số học sinh tham gia ở mỗi môn và tổng số học sinh tham gia = Số học sinh tham gia ở mỗi môn : Tổng số học sinh x 100%.
Lời giải chi tiết:
a)
Môn | Bơi | Võ dân tộc | Bóng ném | Cờ vua |
Học sinh | 24 | 20 | 20 | 36 |
b)
Tỉ số phần trăm của số học sinh tham gia môn Bơi và tổng số học sinh tham gia là :
24 : 100 x 100% = 24%
Tỉ số phần trăm của số học sinh tham gia môn Võ dân tộc và tổng số học sinh tham gia là :
20 : 100 x 100% = 20%
Tỉ số phần trăm của số học sinh tham gia môn Bóng ném và tổng số học sinh tham gia là :
20 : 100 x 100% = 20%
Tỉ số phần trăm của số học sinh tham gia môn Cờ vua và tổng số học sinh tham gia là :
36 : 100 x 100% = 36%
Giải Bài 2 trang 135 VBT Toán 5 tập 1 – Kết nối tri thức với cuộc sống
Viết số thích hợp vào chỗ chấm.
Một bể cá dạng hình hộp chữ nhật có chu vi đáy là 300 cm, chiều dài hơn chiều rộng 30 cm, chiều cao bể cá là 60 cm.
a) - Chiều dài đáy bể cá là .......... cm.
- Chiều rộng đáy bể cá là .......... cm.
b) Biết mực nước ở bể cá là 42 cm.
Lượng nước trong bể chiếm ........% so với lượng nước khi đầy bể.
Phương pháp giải:
a)
- Chiều dài = (Nửa chu vi đáy + Chênh lệch kích thước chiều dài và chiều rộng) : 2.
- Chiều rộng = Nửa chu vi đáy – Chiều dài.
b)
- Thể tích bể cá = Chiều dài x Chiều rộng x Chiều cao.
- Thể tích nước trong bể cá = Chiều dài x Chiều rộng x Chiều cao mực nước.
- Tỉ số phần trăm của lượng nước hiện có trong bể với lượng nước khi đầy bể = Thể tích nước trong bể cá : Thể tích bể cá x 100%.
Lời giải chi tiết:
a)
- Chiều dài đáy bể cá là (300 : 2 + 30) : 2 = 90 cm.
- Chiều rộng đáy bể cá là 300 : 2 – 90 = 60 cm.
b)
Thể tích bể cá là:
90 x 60 x 60 = 324 000 (cm3)
Thể tích nước trong bể cá là:
90 x 60 x 42 = 226 800 (cm3)
Tỉ số phần trăm của lượng nước hiện có trong bể với lượng nước khi đầy bể là:
226 800 : 324 000 = 70%
Lượng nước trong bể chiếm 70% so với lượng nước khi đầy bể.
Giải Bài 3 trang 135 VBT Toán 5 tập 1 – Kết nối tri thức với cuộc sống
Cùng xuất phát ở bến A đi đến khu du lịch B, Việt đi xe buýt thì đến nơi lúc 8 giờ 15 phút, Mai đi xe taxi đến nơi lúc 7 giờ 30 phút. Rô-bốt cho biết cùng trên quãng đường AB, thời gian đi của taxi bằng $\frac{2}{{3}}$ thời gian đi của xe buýt.
a) Tính thời gian của mỗi xe ô tô đi trên quãng đường AB.
b) Tính độ dài quãng đường AB. Biết vận tốc của xe buýt là 40 km/h.
Phương pháp giải:
a)
1. Vẽ sơ đồ: coi thời gian đi của taxi (đóng vai trò số bé) gồm 2 phần bằng nhau thì thời gian của xe buýt (đóng vai trò số lớn) gồm 3 phần bằng nhau như thế.
2. Tìm hiệu số phần bằng nhau.
3. Tìm số bé (lấy giá trị một phần nhân với số phần của số bé).
4. Tìm số lớn (lấy giá trị một phần nhân với số phần của số lớn).
b)
Quãng đường = Vận tốc x Thời gian.
Lời giải chi tiết:
a)
Thời gian đi của xe buýt dài hơn thời gian đi của taxi là:
8 giờ 15 phút - 7 giờ 30 phút = 45 phút = 0,75 (giờ)
Hiệu số phần bằng nhau là:
3 – 2 = 1 (phần)
Thời gian đi xe taxi là:
0,75 : 1 x 2 = 1,5 (giờ)
Thời gian đi xe buýt là:
1,5 + 0,75 = 2,25 (giờ)
b) Độ dài quãng đường AB là:
40 x 2,25 = 90 (km)
Đáp số: a) 1,5 giờ; 2,25 giờ
b) 90 km.
Giải Bài 4 trang 135 VBT Toán 5 tập 1 – Kết nối tri thức với cuộc sống
Viết số thích hợp vào chỗ chấm.
Một tỉnh miền núi có diện tích khoảng 10 000 km2. Hiện tại, mật độ dân số ở tỉnh đó khoảng 80 người/km2 (nghĩa là cứ mỗi ki-lô-mét vuông có trung bình 80 người).
Nếu muốn tăng mật độ dân số của tỉnh đó lên 92 người/km2 thì:
a) Số dân của tỉnh phải tăng thêm ............... người.
b) Số dân phải tăng thêm bằng ........% số dân hiện tại.
Phương pháp giải:
a)
- Số dân của tỉnh với mật độ 80 người/km2 = Diện tích tỉnh x Mật độ dân số.
- Số dân của tỉnh với mật độ 92 người/km2 = Diện tích tỉnh x Mật độ dân số.
- Số dân của tỉnh phải tăng lên để mật độ dân số là 92 người/km2 = Số dân của tỉnh với mật độ 92 người/km2 - Số dân của tỉnh với mật độ 80 người/km2.
b) Phần trăm số dân tăng thêm so với số dân hiện tại = Số dân tăng thêm : Số dân hiện tại x 100%.
Lời giải chi tiết:
a) Số dân của tỉnh với mật độ 80 người/km2 là:
10 000 x 80 = 800 000 (người)
Số dân của tỉnh với mật độ 92 người/km2 là:
10 000 x 92 = 920 000 (người)
Muốn tăng mật độ dân số của tỉnh đó là 92 người/km2 thì số dân của tỉnh phải tăng thêm số người là:
920 000 – 800 000 = 120 000 (người)
Số dân của tỉnh phải tăng thêm 120 000 người.
b)
Số dân tăng thêm chiếm số phần trăm là:
120 000 : 800 000 x 100% = 15%
Số dân phải tăng thêm bằng 15 % số dân hiện tại.
Giải Bài 1 trang 134 VBT Toán 5 tập 1 – Kết nối tri thức với cuộc sống
Biểu đồ dưới đây cho biết số học sinh tham gia bốn môn Cờ vua, Bóng ném, Võ dân tộc, Bơi trong Hội khoẻ Phù Đổng của một trường tiểu học.
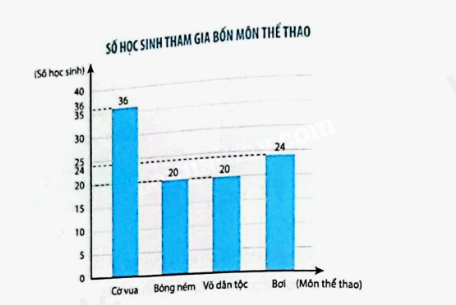
a) Hoàn thành bảng sau.
Môn | Bơi | Võ dân tộc | Bóng ném | Cờ vua |
Học sinh |
b) Tìm tỉ số phần trăm của số học sinh tham gia ở mỗi môn và tổng số học sinh tham gia.
Phương pháp giải:
a) Quan sát biểu đồ rồi trả lời câu hỏi
b) Tỉ số phần trăm của số học sinh tham gia ở mỗi môn và tổng số học sinh tham gia = Số học sinh tham gia ở mỗi môn : Tổng số học sinh x 100%.
Lời giải chi tiết:
a)
Môn | Bơi | Võ dân tộc | Bóng ném | Cờ vua |
Học sinh | 24 | 20 | 20 | 36 |
b)
Tỉ số phần trăm của số học sinh tham gia môn Bơi và tổng số học sinh tham gia là :
24 : 100 x 100% = 24%
Tỉ số phần trăm của số học sinh tham gia môn Võ dân tộc và tổng số học sinh tham gia là :
20 : 100 x 100% = 20%
Tỉ số phần trăm của số học sinh tham gia môn Bóng ném và tổng số học sinh tham gia là :
20 : 100 x 100% = 20%
Tỉ số phần trăm của số học sinh tham gia môn Cờ vua và tổng số học sinh tham gia là :
36 : 100 x 100% = 36%
Bài 75 Ôn tập chung (tiết 4) trang 134 Vở bài tập Toán 5 - Kết nối tri thức là một bài học quan trọng trong giai đoạn ôn tập cuối năm của học sinh lớp 5. Bài học này giúp các em củng cố lại kiến thức đã học trong suốt năm học, chuẩn bị cho kỳ thi cuối năm sắp tới.
Bài 75 tập trung vào việc ôn tập các kiến thức và kỹ năng sau:
Dưới đây là giải chi tiết các bài tập trong Bài 75 Ôn tập chung (tiết 4) trang 134 Vở bài tập Toán 5 - Kết nối tri thức:
Bài 1 yêu cầu học sinh tính nhẩm nhanh các phép tính đơn giản với số thập phân. Ví dụ: 1,5 + 2,3 = ?; 4,8 - 1,2 = ?; 2,5 x 4 = ?; 6,3 : 3 = ?
Để tính nhẩm nhanh, học sinh có thể sử dụng các kỹ năng đã học như làm tròn số, chuyển đổi đơn vị, hoặc sử dụng các quy tắc tính nhẩm.
Bài 2 yêu cầu học sinh thực hiện các phép tính phức tạp hơn với số thập phân. Ví dụ: 3,45 + 2,78 = ?; 5,67 - 1,92 = ?; 1,23 x 4,5 = ?; 7,89 : 2,6 = ?
Khi thực hiện các phép tính này, học sinh cần chú ý đến việc đặt dấu phẩy và chuyển đổi đơn vị. Có thể sử dụng máy tính bỏ túi để kiểm tra kết quả.
Bài 3 là các bài toán có lời văn, yêu cầu học sinh phân tích đề bài, tìm ra các dữ kiện quan trọng và lập kế hoạch giải toán. Ví dụ: Một mảnh đất hình chữ nhật có chiều dài 12,5m và chiều rộng 8,4m. Tính diện tích mảnh đất đó.
Để giải bài toán này, học sinh cần xác định được công thức tính diện tích hình chữ nhật (Diện tích = Chiều dài x Chiều rộng) và thay các giá trị đã cho vào công thức để tính toán.
Bài 75 Ôn tập chung (tiết 4) trang 134 Vở bài tập Toán 5 - Kết nối tri thức là một bài học quan trọng giúp học sinh củng cố kiến thức và kỹ năng đã học trong suốt năm học. Bằng cách ôn tập lại kiến thức, luyện tập thường xuyên, sử dụng tài liệu tham khảo và hỏi thầy cô giáo, học sinh có thể học tốt bài học này và đạt kết quả cao trong kỳ thi cuối năm.