Bài học này giúp các em học sinh ôn tập lại kiến thức về số tự nhiên, phân số và số thập phân đã học trong chương trình Toán 5. Thông qua các bài tập thực hành, các em sẽ củng cố kỹ năng giải toán và áp dụng kiến thức vào thực tế.
Giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu cho từng bài tập trong vở bài tập Toán 5, giúp các em học tập hiệu quả và đạt kết quả tốt nhất.
a) Viết phân số và cách đọc phân số chỉ phần đã tô màu của mỗi hình dưới đây.
Giải Bài 2 trang 97 VBT Toán 5 tập 1 – Kết nối tri thức với cuộc sống
Rút gọn các phân số sau.
$\frac{12}{{27}}$= ………………………; | $\frac{25}{{40}}$ = ………………………; | $\frac{64}{{96}}$ = ……………………… |
Phương pháp giải:
Khi rút gọn phân số có thể làm như sau:
- Xét xem tử số và mẫu số cùng chia hết cho số tự nhiên nào lớn hơn 1.
- Chia tử số và mẫu số cho số đó.
Cứ làm như thế cho đến khi nhận được phân số tối giản.
Lời giải chi tiết:
$\frac{{12}}{{27}} = \frac{{12:3}}{{27:3}} = \frac{4}{9}$
$\frac{{25}}{{40}} = \frac{{25:5}}{{40:5}} = \frac{5}{8}$
$\frac{{64}}{{96}} = \frac{{64:32}}{{96:32}} = \frac{2}{3}$
Giải Bài 3 trang 97 VBT Toán 5 tập 1 – Kết nối tri thức với cuộc sống
Quy đồng mẫu số các phân số sau.
a) $\frac{4}{{7}}$ và $\frac{25}{{49}}$ | b) $\frac{3}{{5}}$; $\frac{5}{{6}}$ và $\frac{23}{{30}}$ |
Phương pháp giải:
- Lấy tử số và mẫu số của phân số thứ nhất nhân với mẫu số của phân số thứ hai.
- Lấy tử số và mẫu số của phân số thứ hai nhân với mẫu số của phân số thứ nhất.
Lời giải chi tiết:
a) $\frac{4}{7}$ và $\frac{{25}}{{49}}$
Chọn mẫu số chung là 49.
Quy đồng mẫu số hai phân số ta có:
$\frac{4}{7} = \frac{{4 \times 7}}{{7 \times 7}} = \frac{{28}}{{49}}$;
$\frac{{25}}{{49}}$ giữ nguyên.
Vậy quy đồng mẫu số hai phân số $\frac{4}{7}$ và $\frac{{25}}{{49}}$ ta được hai phân số $\frac{{28}}{{49}}$ và $\frac{{25}}{{49}}$.
b) $\frac{3}{5}$; $\frac{5}{6}$ và $\frac{{23}}{{30}}$
Chọn mẫu số chung là 30.
Quy đồng mẫu số ba phân số ta có:
$\frac{3}{5} = \frac{{3 \times 6}}{{5 \times 6}} = \frac{{18}}{{30}}$;
$\frac{5}{6} = \frac{{5 \times 5}}{{6 \times 5}} = \frac{{25}}{{30}}$;
$\frac{{25}}{{49}}$ giữ nguyên.
Vậy quy đồng mẫu số ba phân số $\frac{3}{5}$; $\frac{5}{6}$ và $\frac{{23}}{{30}}$ ta được ba phân số $\frac{{18}}{{30}}$; $\frac{{25}}{{30}}$ và $\frac{{23}}{{30}}$
Giải Bài 4 trang 98 VBT Toán 5 tập 1 – Kết nối tri thức với cuộc sống
Viết tiếp vào chỗ chấm cho thích hợp.
Các bạn dành thời gian tập thể dục thể thao vào buổi chiều hằng ngày như sau:
Hòa: $\frac{5}{{12}}$ giờ; Bình: $\frac{1}{3}$ giờ; Trung: $\frac{1}{4}$ giờ; Dũng: $\frac{1}{2}$ giờ.
a) Vậy vào buổi chiều hằng ngày:
– Bạn .............. dành thời gian tập thể dục thể thao nhiều nhất.
– Bạn .............. dành thời gian tập thể dục thể thao ít nhất.
b) Hoà dành thời gian tập thể dục thể thao nhiều hơn các bạn ......................................................
Phương pháp giải:
a) So sánh thời gian tập thể dục thể thao của mỗi bạn, bạn nào có thời gian tập thể dục thể thao lớn nhất thì sẽ dành thời gian thể dục thể thao nhiều nhất và ngược lại
b) So sánh thời gian tập thể dục thể thao của Hòa với các bạn khác.
Lời giải chi tiết:
a) Quy đồng mẫu số các phân số.
Chọn mẫu số chung là 12.
Quy đồng mẫu sỗ các phân số ta có:
$\frac{5}{{12}}$ giữ nguyên; $\frac{1}{3} = \frac{{1 \times 4}}{{3 \times 4}} = \frac{4}{{12}}$; $\frac{1}{4} = \frac{{1 \times 3}}{{4 \times 3}} = \frac{3}{{12}}$; $\frac{1}{2} = \frac{{1 \times 6}}{{2 \times 6}} = \frac{6}{{12}}$.
Vì $\frac{3}{{12}}$ < $\frac{4}{{12}}$ < $\frac{5}{{12}}$ < $\frac{6}{{12}}$ nên $\frac{1}{4}$ < $\frac{1}{3}$ < $\frac{5}{{12}}$ < $\frac{1}{2}$.
Vậy vào buổi chiều hằng ngày:
– Bạn Dũng dành thời gian tập thể dục thể thao nhiều nhất.
– Bạn Trung dành thời gian tập thể dục thể thao ít nhất.
b) Thời gian tập thể dục thể thao của Hòa nhiều hơn thời gian tập thể dục thể thao của Bình và Trung; ít hơn thời gian tập thể dục thể thao của Dũng.
Giải Bài 5 trang 98 VBT Toán 5 tập 1 – Kết nối tri thức với cuộc sống
Khoanh vào chữ đặt trước câu trả lời đúng.
Phân số thập phân $\frac{{459}}{{100}}$viết thành hỗn số là:
A. $45\frac{9}{{100}}$
B. $4\frac{{59}}{{100}}$
C. $400\frac{{59}}{{100}}$
D. $40\frac{{159}}{{100}}$
Phương pháp giải:
- Giữ nguyên mẫu số của phần phân số.
- Tử số bằng số dư của phép chia tử số cho mẫu số.
- Phần nguyên bằng thương của phép chia tử số cho mẫu số.
Lời giải chi tiết:
Ta có 459 : 100 = 4 dư 59.
Vậy $\frac{{459}}{{100}}$ được viết thành hỗn số là $4\frac{{59}}{{100}}$.
Chọn đáp án B.
Giải Bài 1 trang 97 VBT Toán 5 tập 1 – Kết nối tri thức với cuộc sống
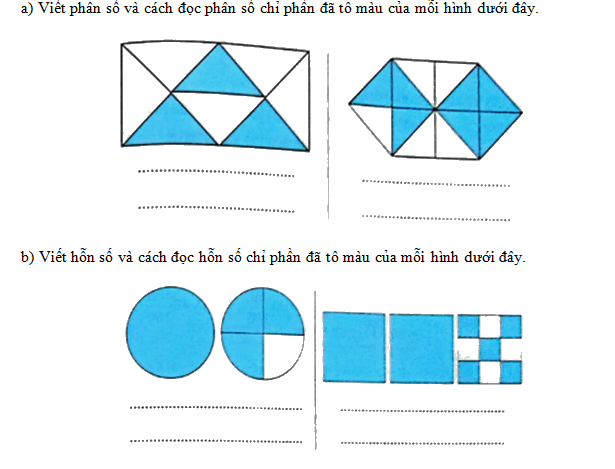
Phương pháp giải:
a)
- Quan sát hình vẽ để viết phân số tương ứng với mỗi hình.
- Trong mỗi phân số, tử số chỉ số phần bằng nhau đã được tô màu và mẫu số chỉ tổng số phần bằng nhau.
b) Khi đọc (hoặc viết) hỗn số ta đọc (hoặc viết) phần nguyên rồi đọc (hoặc viết) phần phân số.
Lời giải chi tiết:
a)
- Hình 1:
+ Viết: $\frac{3}{{8}}$.
+ Đọc: Ba phần tám.
- Hình 2:
+ Viết: $\frac{7}{{12}}$.
+ Đọc: Bảy phần mười hai.
b)
- Hình 1:
+ Viết: $1\frac{3}{4}$.
+ Đọc: Một và ba phần tư.
- Hình 2:
+ Viết: : $2\frac{5}{9}$
+ Đọc: Hai và năm phần chín.
Giải Bài 1 trang 97 VBT Toán 5 tập 1 – Kết nối tri thức với cuộc sống
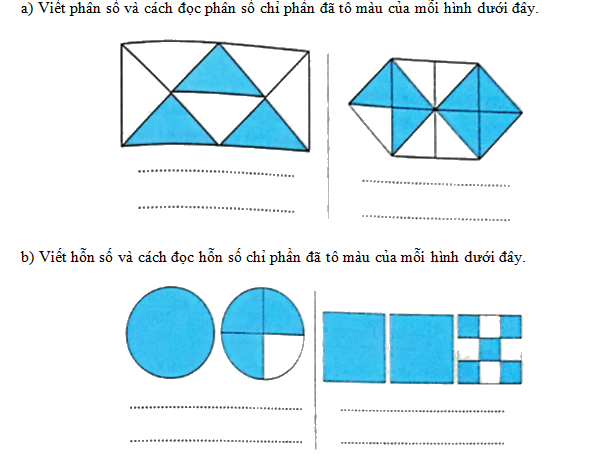
Phương pháp giải:
a)
- Quan sát hình vẽ để viết phân số tương ứng với mỗi hình.
- Trong mỗi phân số, tử số chỉ số phần bằng nhau đã được tô màu và mẫu số chỉ tổng số phần bằng nhau.
b) Khi đọc (hoặc viết) hỗn số ta đọc (hoặc viết) phần nguyên rồi đọc (hoặc viết) phần phân số.
Lời giải chi tiết:
a)
- Hình 1:
+ Viết: $\frac{3}{{8}}$.
+ Đọc: Ba phần tám.
- Hình 2:
+ Viết: $\frac{7}{{12}}$.
+ Đọc: Bảy phần mười hai.
b)
- Hình 1:
+ Viết: $1\frac{3}{4}$.
+ Đọc: Một và ba phần tư.
- Hình 2:
+ Viết: : $2\frac{5}{9}$
+ Đọc: Hai và năm phần chín.
Giải Bài 2 trang 97 VBT Toán 5 tập 1 – Kết nối tri thức với cuộc sống
Rút gọn các phân số sau.
$\frac{12}{{27}}$= ………………………; | $\frac{25}{{40}}$ = ………………………; | $\frac{64}{{96}}$ = ……………………… |
Phương pháp giải:
Khi rút gọn phân số có thể làm như sau:
- Xét xem tử số và mẫu số cùng chia hết cho số tự nhiên nào lớn hơn 1.
- Chia tử số và mẫu số cho số đó.
Cứ làm như thế cho đến khi nhận được phân số tối giản.
Lời giải chi tiết:
$\frac{{12}}{{27}} = \frac{{12:3}}{{27:3}} = \frac{4}{9}$
$\frac{{25}}{{40}} = \frac{{25:5}}{{40:5}} = \frac{5}{8}$
$\frac{{64}}{{96}} = \frac{{64:32}}{{96:32}} = \frac{2}{3}$
Giải Bài 3 trang 97 VBT Toán 5 tập 1 – Kết nối tri thức với cuộc sống
Quy đồng mẫu số các phân số sau.
a) $\frac{4}{{7}}$ và $\frac{25}{{49}}$ | b) $\frac{3}{{5}}$; $\frac{5}{{6}}$ và $\frac{23}{{30}}$ |
Phương pháp giải:
- Lấy tử số và mẫu số của phân số thứ nhất nhân với mẫu số của phân số thứ hai.
- Lấy tử số và mẫu số của phân số thứ hai nhân với mẫu số của phân số thứ nhất.
Lời giải chi tiết:
a) $\frac{4}{7}$ và $\frac{{25}}{{49}}$
Chọn mẫu số chung là 49.
Quy đồng mẫu số hai phân số ta có:
$\frac{4}{7} = \frac{{4 \times 7}}{{7 \times 7}} = \frac{{28}}{{49}}$;
$\frac{{25}}{{49}}$ giữ nguyên.
Vậy quy đồng mẫu số hai phân số $\frac{4}{7}$ và $\frac{{25}}{{49}}$ ta được hai phân số $\frac{{28}}{{49}}$ và $\frac{{25}}{{49}}$.
b) $\frac{3}{5}$; $\frac{5}{6}$ và $\frac{{23}}{{30}}$
Chọn mẫu số chung là 30.
Quy đồng mẫu số ba phân số ta có:
$\frac{3}{5} = \frac{{3 \times 6}}{{5 \times 6}} = \frac{{18}}{{30}}$;
$\frac{5}{6} = \frac{{5 \times 5}}{{6 \times 5}} = \frac{{25}}{{30}}$;
$\frac{{25}}{{49}}$ giữ nguyên.
Vậy quy đồng mẫu số ba phân số $\frac{3}{5}$; $\frac{5}{6}$ và $\frac{{23}}{{30}}$ ta được ba phân số $\frac{{18}}{{30}}$; $\frac{{25}}{{30}}$ và $\frac{{23}}{{30}}$
Giải Bài 4 trang 98 VBT Toán 5 tập 1 – Kết nối tri thức với cuộc sống
Viết tiếp vào chỗ chấm cho thích hợp.
Các bạn dành thời gian tập thể dục thể thao vào buổi chiều hằng ngày như sau:
Hòa: $\frac{5}{{12}}$ giờ; Bình: $\frac{1}{3}$ giờ; Trung: $\frac{1}{4}$ giờ; Dũng: $\frac{1}{2}$ giờ.
a) Vậy vào buổi chiều hằng ngày:
– Bạn .............. dành thời gian tập thể dục thể thao nhiều nhất.
– Bạn .............. dành thời gian tập thể dục thể thao ít nhất.
b) Hoà dành thời gian tập thể dục thể thao nhiều hơn các bạn ......................................................
Phương pháp giải:
a) So sánh thời gian tập thể dục thể thao của mỗi bạn, bạn nào có thời gian tập thể dục thể thao lớn nhất thì sẽ dành thời gian thể dục thể thao nhiều nhất và ngược lại
b) So sánh thời gian tập thể dục thể thao của Hòa với các bạn khác.
Lời giải chi tiết:
a) Quy đồng mẫu số các phân số.
Chọn mẫu số chung là 12.
Quy đồng mẫu sỗ các phân số ta có:
$\frac{5}{{12}}$ giữ nguyên; $\frac{1}{3} = \frac{{1 \times 4}}{{3 \times 4}} = \frac{4}{{12}}$; $\frac{1}{4} = \frac{{1 \times 3}}{{4 \times 3}} = \frac{3}{{12}}$; $\frac{1}{2} = \frac{{1 \times 6}}{{2 \times 6}} = \frac{6}{{12}}$.
Vì $\frac{3}{{12}}$ < $\frac{4}{{12}}$ < $\frac{5}{{12}}$ < $\frac{6}{{12}}$ nên $\frac{1}{4}$ < $\frac{1}{3}$ < $\frac{5}{{12}}$ < $\frac{1}{2}$.
Vậy vào buổi chiều hằng ngày:
– Bạn Dũng dành thời gian tập thể dục thể thao nhiều nhất.
– Bạn Trung dành thời gian tập thể dục thể thao ít nhất.
b) Thời gian tập thể dục thể thao của Hòa nhiều hơn thời gian tập thể dục thể thao của Bình và Trung; ít hơn thời gian tập thể dục thể thao của Dũng.
Giải Bài 5 trang 98 VBT Toán 5 tập 1 – Kết nối tri thức với cuộc sống
Khoanh vào chữ đặt trước câu trả lời đúng.
Phân số thập phân $\frac{{459}}{{100}}$viết thành hỗn số là:
A. $45\frac{9}{{100}}$
B. $4\frac{{59}}{{100}}$
C. $400\frac{{59}}{{100}}$
D. $40\frac{{159}}{{100}}$
Phương pháp giải:
- Giữ nguyên mẫu số của phần phân số.
- Tử số bằng số dư của phép chia tử số cho mẫu số.
- Phần nguyên bằng thương của phép chia tử số cho mẫu số.
Lời giải chi tiết:
Ta có 459 : 100 = 4 dư 59.
Vậy $\frac{{459}}{{100}}$ được viết thành hỗn số là $4\frac{{59}}{{100}}$.
Chọn đáp án B.
Bài 68 trong Vở bài tập Toán 5 Kết nối tri thức là một bài ôn tập quan trọng, giúp học sinh hệ thống lại kiến thức đã học về số tự nhiên, phân số và số thập phân. Bài học này không chỉ kiểm tra khả năng tính toán mà còn đánh giá khả năng vận dụng kiến thức vào giải quyết các bài toán thực tế.
Số tự nhiên là tập hợp các số dùng để đếm. Các số tự nhiên bao gồm 0, 1, 2, 3,... Bài tập ôn tập về số tự nhiên thường xoay quanh các phép tính cộng, trừ, nhân, chia, so sánh số tự nhiên, tìm số lớn nhất, số bé nhất, và các bài toán liên quan đến dãy số tự nhiên.
Ví dụ:
Phân số là biểu thức của một phần của một đơn vị. Một phân số có dạng a/b, trong đó a là tử số và b là mẫu số. Các bài tập ôn tập về phân số thường bao gồm các phép tính cộng, trừ, nhân, chia phân số, so sánh phân số, rút gọn phân số, và tìm phân số bằng nhau.
Ví dụ:
Số thập phân là cách biểu diễn các số không nguyên bằng cách sử dụng dấu phẩy. Các bài tập ôn tập về số thập phân thường bao gồm các phép tính cộng, trừ, nhân, chia số thập phân, so sánh số thập phân, chuyển đổi phân số ra số thập phân và ngược lại.
Ví dụ:
Bài 68 thường có các bài tập kết hợp kiến thức về số tự nhiên, phân số và số thập phân. Các bài tập này yêu cầu học sinh phải vận dụng linh hoạt các kiến thức đã học để giải quyết các tình huống thực tế.
Ví dụ:
Một cửa hàng có 25kg gạo tẻ và 15kg gạo nếp. Hỏi cửa hàng có tất cả bao nhiêu ki-lô-gam gạo?
Một người nông dân thu hoạch được 1/2 tấn thóc. Người đó đã bán 1/3 số thóc thu hoạch được. Hỏi người nông dân còn lại bao nhiêu tấn thóc?
Giaitoan.edu.vn hy vọng rằng với lời giải chi tiết và những hướng dẫn trên, các em học sinh sẽ tự tin hơn khi giải Bài 68: Ôn tập số tự nhiên, phân số, số thập phân (tiết 2) trang 97 Vở bài tập Toán 5 - Kết nối tri thức. Chúc các em học tập tốt!
| Phép tính | Kết quả |
|---|---|
| 1234 + 567 | 1801 |
| 1/2 + 1/3 | 5/6 |
| 1.5 + 2.5 | 4 |
Việc nắm vững kiến thức về số tự nhiên, phân số và số thập phân là nền tảng quan trọng cho việc học toán ở các lớp trên. Hãy dành thời gian ôn tập và thực hành thường xuyên để củng cố kiến thức và nâng cao kỹ năng giải toán.