Bài 3 (5.1) trang 85 Vở thực hành Toán 6 là một bài tập quan trọng trong chương trình học Toán 6, giúp học sinh rèn luyện kỹ năng thực hành về các phép tính với số nguyên. Bài tập này thường yêu cầu học sinh áp dụng các quy tắc cộng, trừ, nhân, chia số nguyên để giải quyết các bài toán cụ thể.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 3 (5.1) trang 85 Vở thực hành Toán 6, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Bài 3(5.1). Hãy chỉ ra trục đối xứng của hình thang cân.
Đề bài
Bài 3(5.1). Hãy chỉ ra trục đối xứng của hình thang cân.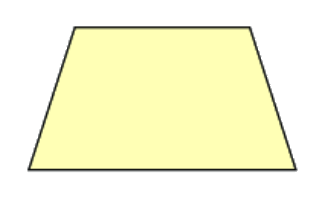
Phương pháp giải - Xem chi tiết
Trục đối xứng là đường thẳng chia hình thành 2 phần mà nếu gấp hình theo đường thẳng đó thì hai phần đó “chồng khít” lên nhau.
Lời giải chi tiết
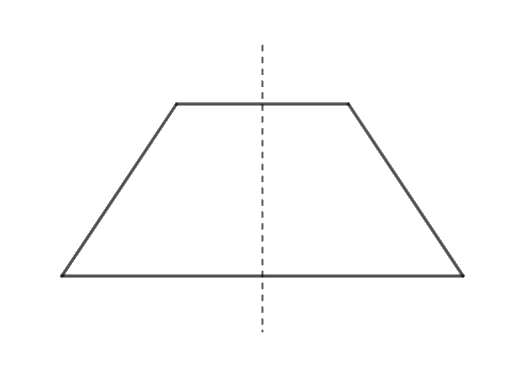
Trục đối xứng của hình thang cân là đường thẳng đi qua trung điểm của 2 cạnh đáy.
Bài 3 (5.1) trang 85 Vở thực hành Toán 6 yêu cầu chúng ta thực hiện các phép tính với số nguyên. Để giải bài tập này một cách hiệu quả, chúng ta cần nắm vững các quy tắc cơ bản về cộng, trừ, nhân, chia số nguyên.
Dưới đây là lời giải chi tiết cho từng phần của bài 3 (5.1) trang 85 Vở thực hành Toán 6:
Áp dụng quy tắc cộng một số nguyên âm và một số nguyên dương, ta có: |-3| = 3, |7| = 7. Vì 7 > 3, nên kết quả là 7 - 3 = 4. Vậy, -3 + 7 = 4.
Áp dụng quy tắc trừ một số nguyên dương và một số nguyên âm, ta đổi dấu -2 thành 2, sau đó cộng 5 + 2 = 7. Vậy, 5 - (-2) = 7.
Áp dụng quy tắc nhân hai số nguyên khác dấu, ta có: |-4| = 4, |3| = 3. Kết quả là 4 * 3 = 12 và đặt dấu âm trước kết quả. Vậy, (-4) * 3 = -12.
Áp dụng quy tắc chia hai số nguyên cùng dấu, ta có: |-12| = 12, |-4| = 4. Kết quả là 12 : 4 = 3 và đặt dấu dương trước kết quả. Vậy, (-12) : (-4) = 3.
Để củng cố kiến thức về các phép tính với số nguyên, các em có thể tự giải các bài tập tương tự sau:
Để học tốt môn Toán, các em cần:
Giaitoan.edu.vn hy vọng rằng với lời giải chi tiết và hướng dẫn cụ thể này, các em học sinh sẽ tự tin hơn trong việc giải các bài tập về số nguyên. Chúc các em học tập tốt!