Bài 3 (5.11) trang 91 Vở thực hành Toán 6 là một bài tập quan trọng trong chương trình học Toán 6, giúp học sinh rèn luyện kỹ năng thực hành và áp dụng kiến thức đã học về các phép tính với số nguyên. Bài tập này thường yêu cầu học sinh thực hiện các phép tính cộng, trừ, nhân, chia số nguyên, kết hợp với các quy tắc ưu tiên thực hiện phép tính.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 3 (5.11) trang 91 Vở thực hành Toán 6, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
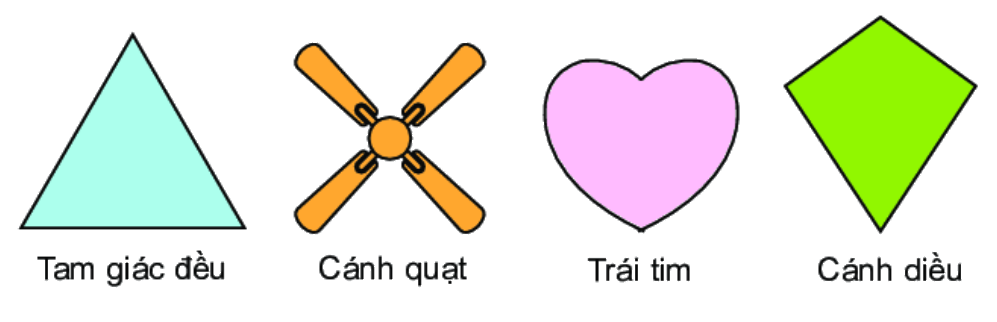
Bài 3 (5.11). Trong các hình dưới đây, hãy chỉ ra: a) Những hình có tâm đối xứng b) Những hình có trục đối xứng
Đề bài
Bài 3 (5.11). Trong các hình dưới đây, hãy chỉ ra:
a) Những hình có tâm đối xứng
b) Những hình có trục đối xứng
Phương pháp giải - Xem chi tiết
- Điểm O được gọi là tâm đối xứng của hình khi quay hình đúng nửa vòng quanh điểm O thì hình thu được chồng khít với chính nó ở vị trí ban đầu.
- Trục đối xứng là đường thẳng chia hình thành 2 phần mà nếu gấp hình theo đường thẳng đó thì hai phần đó “chồng khít” lên nhau.
Lời giải chi tiết
a) Hình có tâm đối xứng là hình cánh quạt
b) Tất cả các hình đều có trục đối xứng.
Bài 3 (5.11) trang 91 Vở thực hành Toán 6 yêu cầu chúng ta thực hiện các phép tính số học. Để giải bài này một cách chính xác, chúng ta cần nắm vững các quy tắc về thứ tự thực hiện các phép tính: nhân, chia trước; cộng, trừ sau. Đồng thời, cần chú ý đến dấu của số nguyên âm và dương.
Thực hiện các phép tính sau:
Chúng ta sẽ giải từng phần của bài tập:
Khi thực hiện các phép tính với số nguyên, cần đặc biệt chú ý đến các điểm sau:
Để trừ một số nguyên, ta cộng số đối của số đó vào số bị trừ. Ví dụ: a - b = a + (-b)
Luôn thực hiện các phép tính nhân, chia trước; cộng, trừ sau. Nếu có dấu ngoặc, thực hiện các phép tính trong ngoặc trước.
Để củng cố kiến thức về các phép tính với số nguyên, các em có thể tự giải thêm các bài tập sau:
Bài 3 (5.11) trang 91 Vở thực hành Toán 6 là một bài tập cơ bản nhưng quan trọng, giúp học sinh làm quen với các phép tính với số nguyên. Việc nắm vững các quy tắc và thực hành thường xuyên sẽ giúp các em giải bài tập một cách nhanh chóng và chính xác.