Bài 1 (4.23) trang 78 Vở thực hành Toán 6 là một bài tập quan trọng trong chương trình học Toán 6, giúp học sinh rèn luyện kỹ năng thực hành và áp dụng kiến thức đã học.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, cùng với các phương pháp giải bài tập hiệu quả, giúp học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Bài 1 (4.23). a) vẽ hình vuông có cạnh 5cm. b) vẽ hình chữ nhật có chiều dài 4cm, chiều rộng 2cm. c) vẽ tam giác đều có cạnh 3cm.
a) vẽ hình vuông có cạnh 5cm.
Phương pháp giải:
a) Hình vuông có 4 cạnh bằng nhau, bốn góc bằng nhau và bằng \({90^o}\)
Lời giải chi tiết:
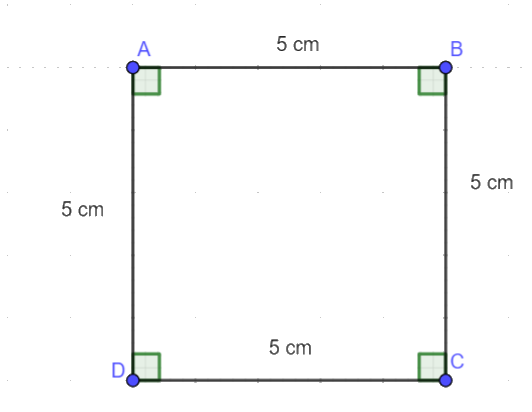
a) Bước 1. Vẽ đoạn thẳng AB = 5 cm.
Bước 2. Vẽ đường thẳng vuông góc với AB tại A. Xác định điểm D trên đường thẳng đó sao cho AD = 5 cm.
Bước 3. Vẽ đường thẳng vuông góc với AB tại B. Xác định điểm C trên đường thẳng đó sao cho BC = 5 cm.
Bước 4. Nối C với D ta được hình vuông ABCD.
b) vẽ hình chữ nhật có chiều dài 4cm, chiều rộng 2cm.
Phương pháp giải:
b) Hình chữ nhật có bốn góc bằng nhau và bằng \({90^o}\), các cạnh đối bằng nhau, hai đường chéo bằng nhau.
Lời giải chi tiết:
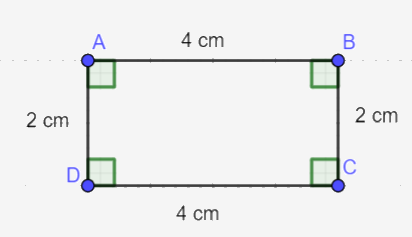
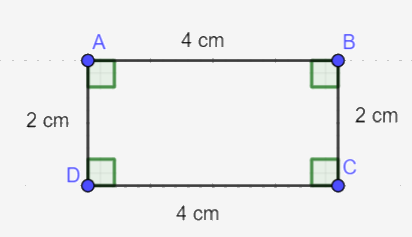
b) Vẽ hình chữ nhật ABCD có một cạnh bằng 4 cm, một cạnh bằng 2 cm theo hướng dẫn sau:
Bước 1. Vẽ đoạn thẳng AB = 4 cm.
Bước 2. Vẽ đường thẳng vuông góc với AB tại A. Trên đường thẳng đó lấy điểm D sao cho AD = 2 cm.
Bước 3. Vẽ đường thẳng vuông góc với AB tại B. Trên đường thẳng đó lấy điểm C sao cho BC = 2 cm.
Bước 4. Nối D với C ta được hình chữ nhật ABCD.
c) vẽ tam giác đều có cạnh 3cm.
Phương pháp giải:
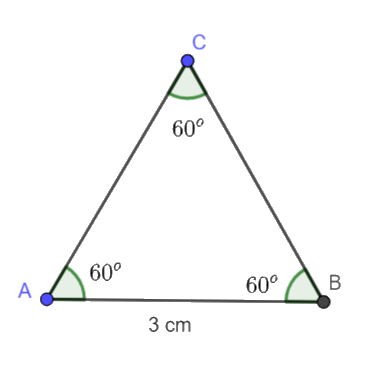
c)Tam giác đều có ba cạnh bằng nhau, ba góc bằng nhau và bằng \({60^o}\)
Lời giải chi tiết:
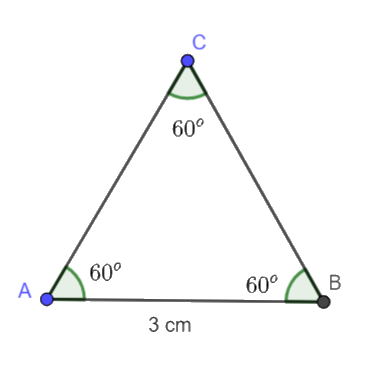
c) Bước 1. Vẽ đoạn thẳng AB = 3 cm.
Bước 2. Dùng ê ke có góc 60o vẽ góc BAx bằng 60o.
Bước 3. Vẽ góc ABy bằng 60o. Ta thấy Ax và By cắt nhau tại C, ta được tam giác đều ABC.
Bài 1 (4.23).
a) vẽ hình vuông có cạnh 5cm.
Phương pháp giải:
a) Hình vuông có 4 cạnh bằng nhau, bốn góc bằng nhau và bằng \({90^o}\)
Lời giải chi tiết:
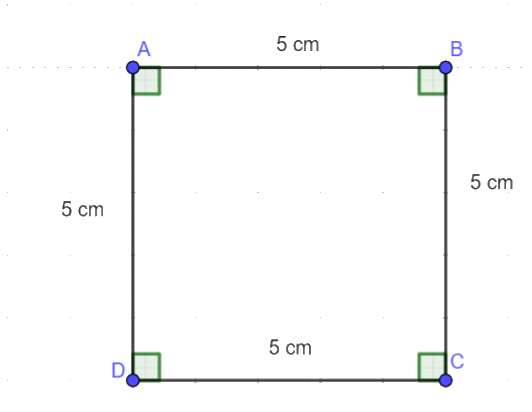
a) Bước 1. Vẽ đoạn thẳng AB = 5 cm.
Bước 2. Vẽ đường thẳng vuông góc với AB tại A. Xác định điểm D trên đường thẳng đó sao cho AD = 5 cm.
Bước 3. Vẽ đường thẳng vuông góc với AB tại B. Xác định điểm C trên đường thẳng đó sao cho BC = 5 cm.
Bước 4. Nối C với D ta được hình vuông ABCD.
b) vẽ hình chữ nhật có chiều dài 4cm, chiều rộng 2cm.
Phương pháp giải:
b) Hình chữ nhật có bốn góc bằng nhau và bằng \({90^o}\), các cạnh đối bằng nhau, hai đường chéo bằng nhau.
Lời giải chi tiết:
b) Vẽ hình chữ nhật ABCD có một cạnh bằng 4 cm, một cạnh bằng 2 cm theo hướng dẫn sau:
Bước 1. Vẽ đoạn thẳng AB = 4 cm.
Bước 2. Vẽ đường thẳng vuông góc với AB tại A. Trên đường thẳng đó lấy điểm D sao cho AD = 2 cm.
Bước 3. Vẽ đường thẳng vuông góc với AB tại B. Trên đường thẳng đó lấy điểm C sao cho BC = 2 cm.
Bước 4. Nối D với C ta được hình chữ nhật ABCD.
c) vẽ tam giác đều có cạnh 3cm.
Phương pháp giải:
c)Tam giác đều có ba cạnh bằng nhau, ba góc bằng nhau và bằng \({60^o}\)
Lời giải chi tiết:
c) Bước 1. Vẽ đoạn thẳng AB = 3 cm.
Bước 2. Dùng ê ke có góc 60o vẽ góc BAx bằng 60o.
Bước 3. Vẽ góc ABy bằng 60o. Ta thấy Ax và By cắt nhau tại C, ta được tam giác đều ABC.
Bài 1 (4.23) trang 78 Vở thực hành Toán 6 thuộc chương trình Toán 6, tập trung vào việc vận dụng các kiến thức về phân số, so sánh phân số, và các phép toán cơ bản với phân số. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm và quy tắc liên quan.
Bài 1 (4.23) trang 78 Vở thực hành Toán 6 thường yêu cầu học sinh thực hiện các thao tác sau:
Để giải bài 1 (4.23) trang 78 Vở thực hành Toán 6, học sinh có thể áp dụng các phương pháp sau:
Giả sử bài tập yêu cầu so sánh hai phân số 2/3 và 3/4. Ta có thể quy đồng mẫu số của hai phân số như sau:
2/3 = 8/12
3/4 = 9/12
Vì 8/12 < 9/12 nên 2/3 < 3/4.
Khi giải bài 1 (4.23) trang 78 Vở thực hành Toán 6, học sinh cần lưu ý những điều sau:
Kiến thức về phân số có ứng dụng rộng rãi trong đời sống hàng ngày, ví dụ như:
Để củng cố kiến thức và kỹ năng, học sinh có thể tự giải thêm các bài tập tương tự trong Vở thực hành Toán 6 và các tài liệu tham khảo khác.
Bài 1 (4.23) trang 78 Vở thực hành Toán 6 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng làm việc với phân số. Bằng cách nắm vững các khái niệm, quy tắc và phương pháp giải bài tập, học sinh có thể tự tin giải quyết các bài toán tương tự và ứng dụng kiến thức vào thực tế.