Bài 2 (8.20) trang 53 Vở thực hành Toán 6 là một bài tập quan trọng trong chương trình học Toán 6, giúp học sinh rèn luyện kỹ năng thực hành và áp dụng kiến thức đã học vào giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 2 (8.20) trang 53 VTH Toán 6, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Bài 2 (8.20). Cho ba điểm A, B, C cùng nằm trên đường thẳng d sao cho B nằm giữa A và C. Hai điểm D và E không thuộc d và không cùng thẳng hàng với điểm nào trong các điểm A, B,C. a) Có bao nhiêu đường thẳng, mỗi đường thẳng đi qua ít nhất hai trong năm điểm đã cho? b) Tìm trên đường thẳng d điểm G sao cho D,E,G thẳng hàng. Có phải khi nào cũng tìm được điểm G như thế hay không?
Đề bài
Bài 2 (8.20). Cho ba điểm A, B, C cùng nằm trên đường thẳng d sao cho B nằm giữa A và C. Hai điểm D và E không thuộc d và không cùng thẳng hàng với điểm nào trong các điểm A, B,C.
a) Có bao nhiêu đường thẳng, mỗi đường thẳng đi qua ít nhất hai trong năm điểm đã cho?
b) Tìm trên đường thẳng d điểm G sao cho D,E,G thẳng hàng. Có phải khi nào cũng tìm được điểm G như thế hay không?
Phương pháp giải - Xem chi tiết
Vẽ hình và quan sát
Lời giải chi tiết
Ta có hình vẽ như hình bên
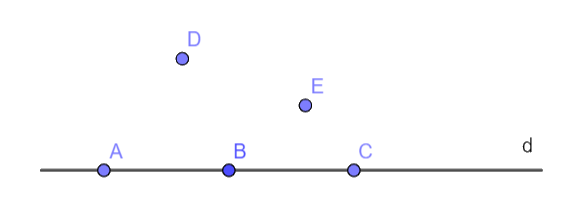
a) Có tất cả 7 đường thẳng mà mỗi đường thẳng tròn số đó đi qua hai trong năm điểm đã cho.
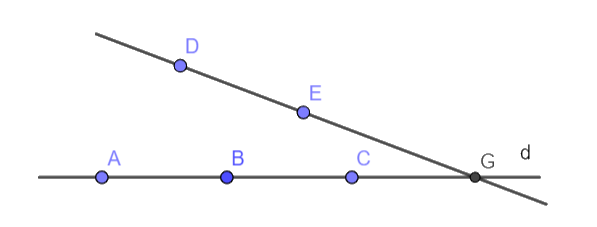
b) Kẻ đường thẳng DE cắt đường thẳng d tại điểm G. Khi đó G chính là điểm nằm trên d thỏa mãn ba điểm D, E, G thẳng hàng.
Nếu đường thẳng DE luôn cắt với đường thẳng d thì ta sẽ tìm được điểm G như vậy.
Bài 2 (8.20) trang 53 Vở thực hành Toán 6 thuộc chương trình học Toán 6, tập trung vào việc vận dụng các kiến thức về số nguyên, phép cộng, trừ, nhân, chia số nguyên để giải quyết các bài toán thực tế. Bài tập này thường yêu cầu học sinh phải phân tích đề bài, xác định đúng các yếu tố cần tìm và lựa chọn phương pháp giải phù hợp.
Để bắt đầu, chúng ta cùng xem lại đề bài của bài 2 (8.20) trang 53 Vở thực hành Toán 6:
(Đề bài cụ thể sẽ được chèn vào đây - ví dụ: Tính: a) (-3) + 5; b) 8 + (-2); c) (-7) + (-1); d) 0 + (-4))
Để giải các bài tập về số nguyên, học sinh cần nắm vững các quy tắc sau:
Dựa trên các quy tắc trên, chúng ta sẽ tiến hành giải chi tiết từng phần của bài 2 (8.20) trang 53 Vở thực hành Toán 6:
Để củng cố kiến thức và kỹ năng giải bài tập về số nguyên, các em học sinh có thể luyện tập thêm các bài tập tương tự sau:
Để giải bài tập về số nguyên một cách hiệu quả, các em học sinh nên:
Bài 2 (8.20) trang 53 Vở thực hành Toán 6 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải bài tập về số nguyên. Hy vọng với hướng dẫn chi tiết và dễ hiểu trên, các em học sinh sẽ tự tin giải bài tập này và đạt kết quả tốt trong môn Toán.