Chào mừng các em học sinh đến với bài giải bài 24 Toán 4 Kết nối tri thức. Bài học hôm nay sẽ giúp các em hiểu rõ hơn về tính chất giao hoán và tính chất kết hợp của phép cộng, những kiến thức nền tảng quan trọng trong chương trình Toán học.
giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu, giúp các em tự tin làm bài tập và nắm vững kiến thức.
Không thực hiện phép tính, hãy viết kết quả của các phép cộng sau. 871 + 918 = 1 789 Cho biểu thức chứa chữ a + b + c. Tô màu các tấm bảng dưới đây ghi biểu thức có giá trị bằng biểu thức đã cho.
Không thực hiện phép tính, hãy viết kết quả của các phép cộng sau.
871 + 918 = 1 789
918 + 871 = ...........
6 311 + 1 949 = 8 260
1 949 + 6 311 = ...........
84 + 8 371 = 8 455
8 371 + 84 = ...........
Phương pháp giải:
Tính chất giao hoán: Khi đổi chỗ các số hạng trong một tổng thì tổng không thay đổi
a + b = b + a
Lời giải chi tiết:
871 + 918 = 1 789
918 + 871 = 1 789
6311 + 1 949 = 8 260
1 949 + 6 311 = 8 260
84 + 8 371 = 8 455
8 371 + 84 = 8 455
Tính bằng cách thuận tiện.
a) 8 + 9 + 2
b) 28 + 93 + 72
c) 90 + 76 + 10
d) 50 + 98 + 50
Phương pháp giải:
Áp dụng tính chất giao hoán để đổi chỗ các số hạng có tổng là số tròn chục, tròn trăm đứng cạnh nhau
Lời giải chi tiết:

Cho biểu thức chứa chữ a + b + c. Tô màu các tấm bảng dưới đây ghi biểu thức có giá trị bằng biểu thức đã cho.

Phương pháp giải:
Tính chất giao hoán: Khi đổi chỗ các số hạng trong một tổng thì tổng không thay đổi.
Lời giải chi tiết:
Ta có: a + c + b = b + a + c
Học sinh tô màu vào các tấm bảng ghi biểu thức: a + c + b và b + a + c
Không thực hiện phép tính, hãy nối các biểu thức có giá trị bằng nhau.
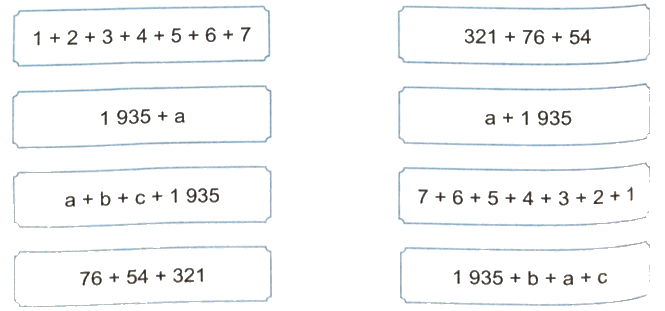
Phương pháp giải:
Áp dụng tính chất giao hoán: Khi đổi chỗ các số hạng trong một tổng thì tổng không thay đổi.
Lời giải chi tiết:
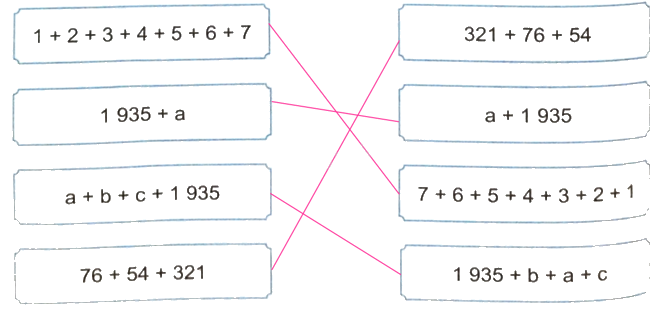
Không thực hiện phép tính, hãy viết kết quả của các phép cộng sau.
871 + 918 = 1 789
918 + 871 = ...........
6 311 + 1 949 = 8 260
1 949 + 6 311 = ...........
84 + 8 371 = 8 455
8 371 + 84 = ...........
Phương pháp giải:
Tính chất giao hoán: Khi đổi chỗ các số hạng trong một tổng thì tổng không thay đổi
a + b = b + a
Lời giải chi tiết:
871 + 918 = 1 789
918 + 871 = 1 789
6311 + 1 949 = 8 260
1 949 + 6 311 = 8 260
84 + 8 371 = 8 455
8 371 + 84 = 8 455
Cho biểu thức chứa chữ a + b + c. Tô màu các tấm bảng dưới đây ghi biểu thức có giá trị bằng biểu thức đã cho.

Phương pháp giải:
Tính chất giao hoán: Khi đổi chỗ các số hạng trong một tổng thì tổng không thay đổi.
Lời giải chi tiết:
Ta có: a + c + b = b + a + c
Học sinh tô màu vào các tấm bảng ghi biểu thức: a + c + b và b + a + c
Không thực hiện phép tính, hãy nối các biểu thức có giá trị bằng nhau.
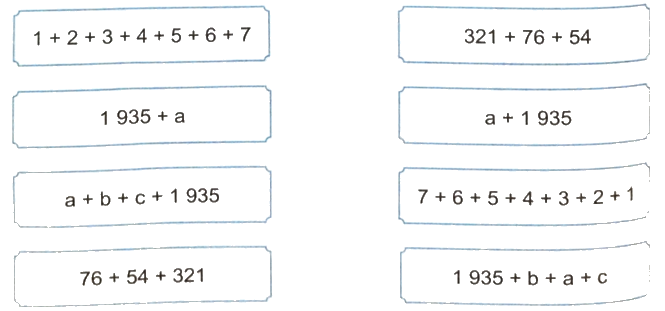
Phương pháp giải:
Áp dụng tính chất giao hoán: Khi đổi chỗ các số hạng trong một tổng thì tổng không thay đổi.
Lời giải chi tiết:
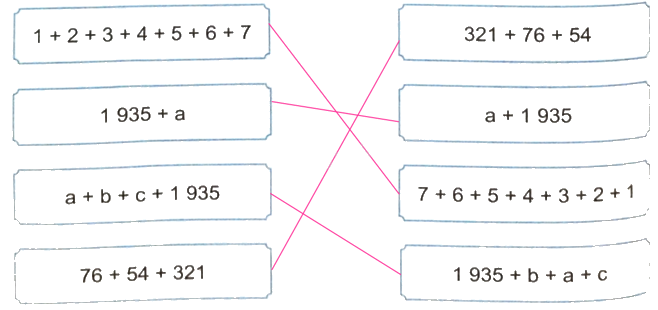
Tính bằng cách thuận tiện.
a) 8 + 9 + 2
b) 28 + 93 + 72
c) 90 + 76 + 10
d) 50 + 98 + 50
Phương pháp giải:
Áp dụng tính chất giao hoán để đổi chỗ các số hạng có tổng là số tròn chục, tròn trăm đứng cạnh nhau
Lời giải chi tiết:

Bài 24 trong Vở bài tập Toán 4 Kết nối tri thức tập trung vào việc củng cố kiến thức về tính chất giao hoán và tính chất kết hợp của phép cộng. Đây là hai tính chất quan trọng giúp đơn giản hóa các phép tính và giải quyết các bài toán một cách hiệu quả hơn.
Tính chất giao hoán của phép cộng khẳng định rằng việc thay đổi vị trí của các số hạng trong một phép cộng không làm thay đổi kết quả. Công thức tổng quát: a + b = b + a
Ví dụ: 5 + 3 = 3 + 5 = 8
Tính chất kết hợp của phép cộng cho phép ta nhóm các số hạng theo nhiều cách khác nhau mà vẫn giữ nguyên kết quả. Công thức tổng quát: (a + b) + c = a + (b + c)
Ví dụ: (2 + 4) + 1 = 2 + (4 + 1) = 7
Ví dụ: 12 + 15 + 8
Cách 1: 12 + 15 + 8 = 27 + 8 = 35
Cách 2: 12 + 15 + 8 = 12 + (15 + 8) = 12 + 23 = 35
a) 15 + 23 = 23 + ... (15)
b) (10 + 5) + 7 = 10 + (5 + ...)(7)
Để hiểu sâu hơn về tính chất giao hoán và tính chất kết hợp, các em có thể thực hành thêm với các bài tập sau:
Việc nắm vững tính chất giao hoán và tính chất kết hợp của phép cộng là rất quan trọng trong quá trình học Toán. Các em hãy luyện tập thường xuyên để có thể áp dụng linh hoạt các tính chất này vào giải quyết các bài toán một cách nhanh chóng và chính xác.
giaitoan.edu.vn hy vọng bài giải này sẽ giúp các em học tốt môn Toán 4. Chúc các em học tập tốt!