Bài 55 thuộc chương trình Toán 4 Kết nối tri thức với cuộc sống, tập trung vào việc ôn lại và củng cố kiến thức về tính chất cơ bản của phân số. Bài học này giúp học sinh hiểu rõ hơn về cách rút gọn phân số, quy đồng mẫu số và so sánh phân số.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho từng phần của bài tập, giúp học sinh tự tin giải quyết các bài toán tương tự.
Cùng giảm 5 lần tử số và mẫu số của phân số trong tấm thẻ bên ... Khoanh vào các phân số bằng nhau trong các phân số sau 4/6
Khoanh vào các phân số bằng nhau trong các phân số sau.
$\frac{4}{6}$ ; $\frac{3}{2}$ ; $\frac{8}{{12}}$ ; $\frac{2}{3}$
Phương pháp giải:
Nếu chia cả tử số và mẫu số của một phân số cho cùng một số tự nhiên khác 0 thì được một phân số bằng phân số đã cho.
Lời giải chi tiết:
Ta có: $\frac{4}{6} = \frac{{4:2}}{{6:2}} = \frac{2}{3}$; $\frac{8}{{12}} = \frac{{8:4}}{{12:4}} = \frac{2}{3}$
Vậy các phân số bằng nhau là: $\frac{4}{6};\frac{8}{{12}};\frac{2}{3}$
Khoanh vào chữ đặt trước câu trả lời đúng.
Cùng giảm 5 lần tử số và mẫu số của phân số trong tấm thẻ bên, ta được phân số nào bằng phân số trong tấm thẻ đó?

A. $\frac{{12}}{{95}}$
B.$\frac{{60}}{{19}}$
C. $\frac{{12}}{{19}}$
D. $\frac{{19}}{{12}}$
Phương pháp giải:
Nếu chia cả tử số và mẫu số của một phân số cho cùng một số tự nhiên khác 0 thì được một phân số bằng phân số đã cho.
Lời giải chi tiết:
Ta có: $\frac{{60}}{{95}} = \frac{{60:5}}{{95:5}} = \frac{{12}}{{19}}$
Chọn C
Số?
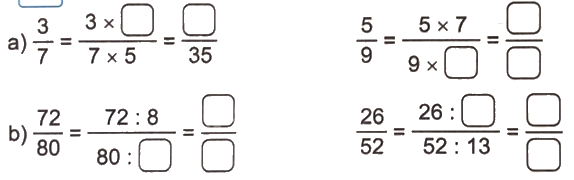
Phương pháp giải:
- Nếu nhân cả tử số và mẫu số của một phân số với cùng một số tự nhiên khác 0 thì được một phân số bằng phân số đã cho.
- Nếu chia hết cả tử và mẫu số của một phân số cho cùng một số tự nhiên khác 0 thì được một phân số bằng phân số đã cho.
Lời giải chi tiết:
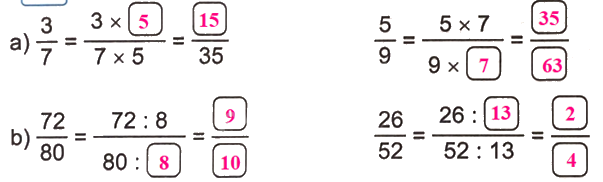
Số?
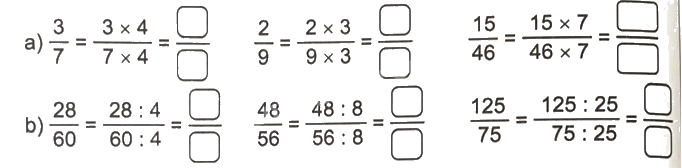
Phương pháp giải:
- Nếu nhân cả tử số và mẫu số của một phân số với cùng một số tự nhiên khác 0 thì được một phân số bằng phân số đã cho.
- Nếu chia hết cả tử và mẫu số của một phân số cho cùng một số tự nhiên khác 0 thì được một phân số bằng phân số đã cho.
Lời giải chi tiết:
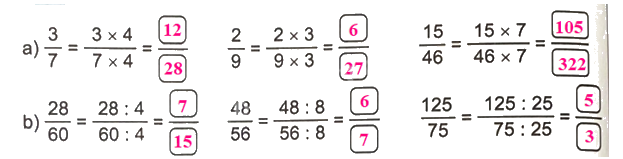
Số?
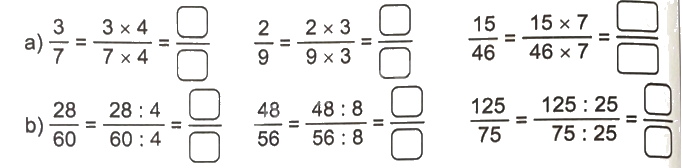
Phương pháp giải:
- Nếu nhân cả tử số và mẫu số của một phân số với cùng một số tự nhiên khác 0 thì được một phân số bằng phân số đã cho.
- Nếu chia hết cả tử và mẫu số của một phân số cho cùng một số tự nhiên khác 0 thì được một phân số bằng phân số đã cho.
Lời giải chi tiết:
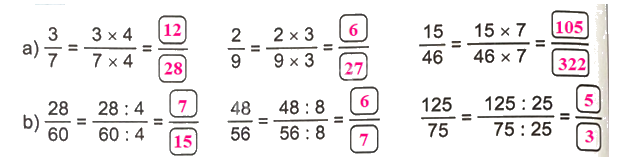
Số?
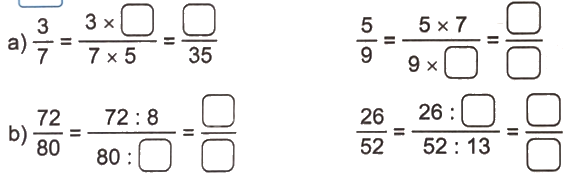
Phương pháp giải:
- Nếu nhân cả tử số và mẫu số của một phân số với cùng một số tự nhiên khác 0 thì được một phân số bằng phân số đã cho.
- Nếu chia hết cả tử và mẫu số của một phân số cho cùng một số tự nhiên khác 0 thì được một phân số bằng phân số đã cho.
Lời giải chi tiết:
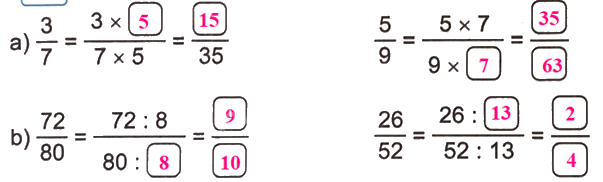
Khoanh vào chữ đặt trước câu trả lời đúng.
Cùng giảm 5 lần tử số và mẫu số của phân số trong tấm thẻ bên, ta được phân số nào bằng phân số trong tấm thẻ đó?

A. $\frac{{12}}{{95}}$
B.$\frac{{60}}{{19}}$
C. $\frac{{12}}{{19}}$
D. $\frac{{19}}{{12}}$
Phương pháp giải:
Nếu chia cả tử số và mẫu số của một phân số cho cùng một số tự nhiên khác 0 thì được một phân số bằng phân số đã cho.
Lời giải chi tiết:
Ta có: $\frac{{60}}{{95}} = \frac{{60:5}}{{95:5}} = \frac{{12}}{{19}}$
Chọn C
Khoanh vào các phân số bằng nhau trong các phân số sau.
$\frac{4}{6}$ ; $\frac{3}{2}$ ; $\frac{8}{{12}}$ ; $\frac{2}{3}$
Phương pháp giải:
Nếu chia cả tử số và mẫu số của một phân số cho cùng một số tự nhiên khác 0 thì được một phân số bằng phân số đã cho.
Lời giải chi tiết:
Ta có: $\frac{4}{6} = \frac{{4:2}}{{6:2}} = \frac{2}{3}$; $\frac{8}{{12}} = \frac{{8:4}}{{12:4}} = \frac{2}{3}$
Vậy các phân số bằng nhau là: $\frac{4}{6};\frac{8}{{12}};\frac{2}{3}$
Bài 55 trong Vở bài tập Toán 4 Kết nối tri thức với cuộc sống là một bài học quan trọng giúp học sinh nắm vững kiến thức nền tảng về phân số. Bài học này tập trung vào việc ôn tập và củng cố các tính chất cơ bản của phân số, bao gồm tính chất rút gọn phân số, quy đồng mẫu số và so sánh phân số.
Bài 55 bao gồm các dạng bài tập sau:
Để rút gọn phân số, ta chia cả tử số và mẫu số của phân số đó cho ước chung lớn nhất của chúng. Ví dụ:
Rút gọn phân số \frac{12}{18}
Ước chung lớn nhất của 12 và 18 là 6. Ta chia cả tử số và mẫu số cho 6:
\frac{12 : 6}{18 : 6} = \frac{2}{3}
Vậy phân số \frac{12}{18} rút gọn thành \frac{2}{3}
Để quy đồng mẫu số các phân số, ta tìm bội chung nhỏ nhất của các mẫu số, sau đó nhân cả tử số và mẫu số của mỗi phân số với một số sao cho mẫu số của chúng bằng bội chung nhỏ nhất đó. Ví dụ:
Quy đồng mẫu số các phân số \frac{1}{2} và \frac{1}{3}
Bội chung nhỏ nhất của 2 và 3 là 6. Ta nhân cả tử số và mẫu số của phân số \frac{1}{2} với 3 và nhân cả tử số và mẫu số của phân số \frac{1}{3} với 2:
\frac{1 \times 3}{2 \times 3} = \frac{3}{6} và \frac{1 \times 2}{3 \times 2} = \frac{2}{6}
Vậy các phân số \frac{1}{2} và \frac{1}{3} quy đồng mẫu số thành \frac{3}{6} và \frac{2}{6}
Để so sánh các phân số, ta có thể quy đồng mẫu số của chúng, sau đó so sánh các tử số. Phân số nào có tử số lớn hơn thì phân số đó lớn hơn. Ví dụ:
So sánh các phân số \frac{2}{5} và \frac{3}{5}
Vì hai phân số này có cùng mẫu số, ta chỉ cần so sánh các tử số. Ta thấy 2 < 3, vậy \frac{2}{5} < \frac{3}{5}
Để nắm vững kiến thức về tính chất cơ bản của phân số, các em học sinh nên luyện tập thêm các bài tập tương tự trong sách bài tập và các tài liệu tham khảo khác. Ngoài ra, các em có thể tham khảo các bài giảng trực tuyến và các video hướng dẫn trên internet.
Bài 55: Tính chất cơ bản của phân số (tiết 1) trang 62 Vở bài tập Toán 4 - Kết nối tri thức với cuộc sống là một bài học quan trọng giúp học sinh củng cố kiến thức về phân số. Việc nắm vững các tính chất cơ bản của phân số là nền tảng để học sinh giải quyết các bài toán phức tạp hơn trong chương trình Toán 4.