Bài 64 thuộc chương trình Toán 4 Kết nối tri thức với cuộc sống, tập trung vào việc giới thiệu và thực hành phép chia phân số. Bài học này giúp học sinh nắm vững kiến thức cơ bản về phân số và cách thực hiện phép chia một cách chính xác.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho bài 64, giúp học sinh tự tin giải quyết các bài tập và hiểu sâu hơn về phép chia phân số.
Viết tiếp vào chỗ chấm cho thích hợp. Bức tranh hình chữ nhật ABCD có diện tích là 66/5 dm2 ... Tô màu vào con cá ghi phép tính có kết quả không phải lớn nhất
a) Viết phân số thích hợp vào chỗ chấm.
Phân số đảo ngược của $\frac{5}{4}$ là: …… Phân số đảo ngược của $\frac{1}{9}$ là: ……
b) Tính.
$\frac{{17}}{6}:\frac{5}{4} = ....................$
$\frac{{21}}{2}:\frac{{13}}{9} = ...................$
$\frac{1}{8}:\frac{1}{9} = ......................$
Phương pháp giải:
a) Viết phân số đảo ngược của mỗi phân số đã cho
b)Muốn thực hiện phép chia hai phân số, ta lấy phân số thứ nhất nhân với phân số đảo ngược của phân số thứ hai
Lời giải chi tiết:
a) Phân số đảo ngược của $\frac{5}{4}$ là: $\frac{4}{5}$. Phân số đảo ngược của $\frac{1}{9}$ là: $\frac{9}{1}$
b) $\frac{{17}}{6}:\frac{5}{4} = \frac{{17}}{6} \times \frac{4}{5} = \frac{{68}}{{30}} = \frac{{34}}{{15}}$
$\frac{{21}}{2}:\frac{{13}}{9} = \frac{{21}}{2} \times \frac{9}{{13}} = \frac{{189}}{{26}}$
$\frac{1}{8}:\frac{1}{9} = \frac{1}{8} \times 9 = \frac{9}{8}$
Viết tiếp vào chỗ chấm cho thích hợp.

Bức tranh hình chữ nhật ABCD có diện tích là $\frac{{66}}{5}$ dm2 và chiều rộng $\frac{{11}}{5}$dm.
a) Chiều dài của bức tranh là ………..dm
b) Anh Long lắp một cái móc treo ở trung điểm I của cạnh AB. Điểm I cách điểm A …….. dm.
Phương pháp giải:
a) Chiều dài của bức tranh = diện tích : chiều rộng
b) Điểm I cách điểm A = chiều dài : 2
Lời giải chi tiết:
a) Chiều dài của bức tranh là: $\frac{{66}}{5}:\frac{{11}}{5} = 6$(dm)
b) Ta có 6 : 2 = 3
Vậy anh Long móc một cái móc treo ở trung điểm I của cạnh AB. Điểm I cách điểm A 3 dm.
Tô màu vào con cá ghi phép tính có kết quả không phải lớn nhất và không phải bé nhất.

Phương pháp giải:
Thực hiện các phép tính, so sánh rồi tô màu theo yêu cầu của bài toán.
Lời giải chi tiết:
Ta có: $\frac{{23}}{5} \times \frac{3}{4} = \frac{{23 \times 3}}{{5 \times 4}} = \frac{{69}}{{20}}$
$\frac{{23}}{5}:\frac{3}{4} = \frac{{23}}{5} \times \frac{4}{3} = \frac{{23 \times 4}}{{5 \times 3}} = \frac{{92}}{{15}}$
$\frac{{14}}{{20}} \times 5 = \frac{{14 \times 5}}{{20}} = \frac{{70}}{{20}} = \frac{7}{2}$
Quy đồng các phân số với mẫu số chung là 60
Ta có: $\frac{{69}}{{20}} = \frac{{207}}{{60}}$ ; $\frac{{92}}{{15}} = \frac{{368}}{{60}}$ ; $\frac{7}{2} = \frac{{210}}{{60}}$
Ta có: $\frac{{207}}{{60}} < \frac{{210}}{{60}} < \frac{{368}}{{60}}$ hay $\frac{{69}}{{20}} < \frac{7}{2} < \frac{{92}}{{15}}$
Vậy con cá ghi phép tính có kết quả không phải lớn nhất và không phải bé nhất là con cá $\frac{{14}}{{20}} \times 5$
Học sinh tự tô màu.
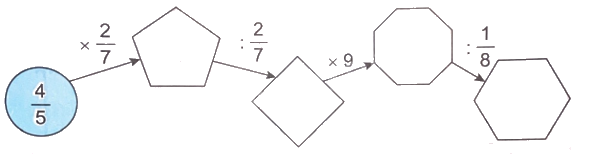
Viết phân số thích hợp vào ô trống.
Phương pháp giải:
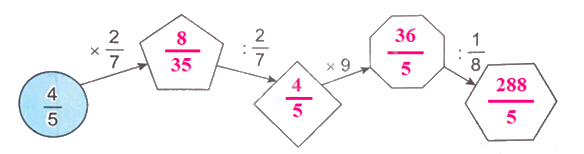
Thực hiện các phép tính theo chiều mũi tên rồi điền phân số thích hợp vào ô trống.
Lời giải chi tiết:
$\frac{4}{5} \times \frac{2}{7} = \frac{8}{{35}}$
$\frac{8}{{35}}:\frac{2}{7} = \frac{8}{{35}} \times \frac{7}{2} = \frac{{56}}{{70}} = \frac{4}{5}$
$\frac{4}{5} \times 9 = \frac{{4 \times 9}}{5} = \frac{{36}}{5}$
$\frac{{36}}{5}:\frac{1}{8} = \frac{{36}}{5} \times 8 = \frac{{288}}{5}$
a) Viết phân số thích hợp vào chỗ chấm.
Phân số đảo ngược của $\frac{5}{4}$ là: …… Phân số đảo ngược của $\frac{1}{9}$ là: ……
b) Tính.
$\frac{{17}}{6}:\frac{5}{4} = ....................$
$\frac{{21}}{2}:\frac{{13}}{9} = ...................$
$\frac{1}{8}:\frac{1}{9} = ......................$
Phương pháp giải:
a) Viết phân số đảo ngược của mỗi phân số đã cho
b)Muốn thực hiện phép chia hai phân số, ta lấy phân số thứ nhất nhân với phân số đảo ngược của phân số thứ hai
Lời giải chi tiết:
a) Phân số đảo ngược của $\frac{5}{4}$ là: $\frac{4}{5}$. Phân số đảo ngược của $\frac{1}{9}$ là: $\frac{9}{1}$
b) $\frac{{17}}{6}:\frac{5}{4} = \frac{{17}}{6} \times \frac{4}{5} = \frac{{68}}{{30}} = \frac{{34}}{{15}}$
$\frac{{21}}{2}:\frac{{13}}{9} = \frac{{21}}{2} \times \frac{9}{{13}} = \frac{{189}}{{26}}$
$\frac{1}{8}:\frac{1}{9} = \frac{1}{8} \times 9 = \frac{9}{8}$
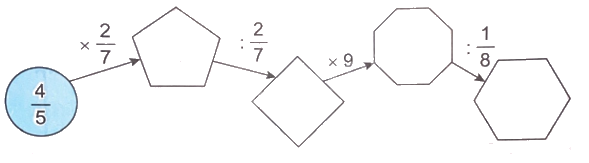
Viết phân số thích hợp vào ô trống.
Phương pháp giải:
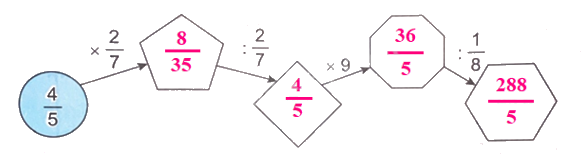
Thực hiện các phép tính theo chiều mũi tên rồi điền phân số thích hợp vào ô trống.
Lời giải chi tiết:
$\frac{4}{5} \times \frac{2}{7} = \frac{8}{{35}}$
$\frac{8}{{35}}:\frac{2}{7} = \frac{8}{{35}} \times \frac{7}{2} = \frac{{56}}{{70}} = \frac{4}{5}$
$\frac{4}{5} \times 9 = \frac{{4 \times 9}}{5} = \frac{{36}}{5}$
$\frac{{36}}{5}:\frac{1}{8} = \frac{{36}}{5} \times 8 = \frac{{288}}{5}$
Viết tiếp vào chỗ chấm cho thích hợp.

Bức tranh hình chữ nhật ABCD có diện tích là $\frac{{66}}{5}$ dm2 và chiều rộng $\frac{{11}}{5}$dm.
a) Chiều dài của bức tranh là ………..dm
b) Anh Long lắp một cái móc treo ở trung điểm I của cạnh AB. Điểm I cách điểm A …….. dm.
Phương pháp giải:
a) Chiều dài của bức tranh = diện tích : chiều rộng
b) Điểm I cách điểm A = chiều dài : 2
Lời giải chi tiết:
a) Chiều dài của bức tranh là: $\frac{{66}}{5}:\frac{{11}}{5} = 6$(dm)
b) Ta có 6 : 2 = 3
Vậy anh Long móc một cái móc treo ở trung điểm I của cạnh AB. Điểm I cách điểm A 3 dm.
Tô màu vào con cá ghi phép tính có kết quả không phải lớn nhất và không phải bé nhất.

Phương pháp giải:
Thực hiện các phép tính, so sánh rồi tô màu theo yêu cầu của bài toán.
Lời giải chi tiết:
Ta có: $\frac{{23}}{5} \times \frac{3}{4} = \frac{{23 \times 3}}{{5 \times 4}} = \frac{{69}}{{20}}$
$\frac{{23}}{5}:\frac{3}{4} = \frac{{23}}{5} \times \frac{4}{3} = \frac{{23 \times 4}}{{5 \times 3}} = \frac{{92}}{{15}}$
$\frac{{14}}{{20}} \times 5 = \frac{{14 \times 5}}{{20}} = \frac{{70}}{{20}} = \frac{7}{2}$
Quy đồng các phân số với mẫu số chung là 60
Ta có: $\frac{{69}}{{20}} = \frac{{207}}{{60}}$ ; $\frac{{92}}{{15}} = \frac{{368}}{{60}}$ ; $\frac{7}{2} = \frac{{210}}{{60}}$
Ta có: $\frac{{207}}{{60}} < \frac{{210}}{{60}} < \frac{{368}}{{60}}$ hay $\frac{{69}}{{20}} < \frac{7}{2} < \frac{{92}}{{15}}$
Vậy con cá ghi phép tính có kết quả không phải lớn nhất và không phải bé nhất là con cá $\frac{{14}}{{20}} \times 5$
Học sinh tự tô màu.
Bài 64 trong Vở bài tập Toán 4 Kết nối tri thức với cuộc sống là bước khởi đầu quan trọng để học sinh làm quen với phép chia phân số. Đây là một khái niệm toán học cơ bản nhưng lại đóng vai trò quan trọng trong việc xây dựng nền tảng toán học vững chắc cho các em.
Thông qua bài học này, học sinh sẽ:
Bài 64 được chia thành các phần chính sau:
Dưới đây là lời giải chi tiết cho các bài tập trong bài 64:
a) \frac{2}{3} : 2 = \frac{2}{3} \times \frac{1}{2} = \frac{1}{3}
b) \frac{3}{4} : 3 = \frac{3}{4} \times \frac{1}{3} = \frac{1}{4}
c) \frac{5}{6} : 5 = \frac{5}{6} \times \frac{1}{5} = \frac{1}{6}
a) \frac{1}{2} : \frac{1}{3} = \frac{1}{2} \times \frac{3}{1} = \frac{3}{2}
b) \frac{2}{5} : \frac{1}{2} = \frac{2}{5} \times \frac{2}{1} = \frac{4}{5}
c) \frac{3}{7} : \frac{2}{3} = \frac{3}{7} \times \frac{3}{2} = \frac{9}{14}
Để củng cố kiến thức về phép chia phân số, bạn có thể luyện tập thêm với các bài tập sau:
Hy vọng với lời giải chi tiết và những hướng dẫn trên, các em học sinh sẽ tự tin hơn khi giải bài 64 và các bài tập liên quan đến phép chia phân số. Chúc các em học tốt!