Bài 56 trong chương trình Toán 4 Kết nối tri thức với cuộc sống tập trung vào việc rèn luyện kỹ năng rút gọn phân số. Đây là một kỹ năng quan trọng giúp học sinh đơn giản hóa các biểu thức toán học và hiểu rõ hơn về giá trị của phân số.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho bài tập này, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Nối hai phân số bằng nhau (theo mẫu). Cho các phân số 2/6, 19/21 ....
Cho các phân số: $\frac{2}{6}$ ; $\frac{{19}}{{21}}$ ; $\frac{{25}}{{17}}$ ; $\frac{{13}}{{42}}$ ; $\frac{{20}}{{35}}$ ; $\frac{{27}}{{57}}$
a) Viết tiếp vào chỗ chấm cho thích hợp.
- Các phân số tối giản là: ………………………………..
- Các phân số chưa tối giản là: ……………………………………….
b) Rút gọn các phân số chưa tối giản ở câu a.
Phương pháp giải:
a)Phân số tối giản là phân số mà tử số và mẫu số không cùng chia hết cho số tự nhiên nào lớn hơn 1.
b) Cách rút gọn phân số:
- Xét xem tử số và mẫu số cùng chia hết cho số tự nhiên nào lớn hơn 1.
- Chia tử số và mẫu số cho số đó.
Cứ làm như thế cho đến khi nhận được phân số tối giản
Lời giải chi tiết:
a)
- Các phân số tối giản là: $\frac{{19}}{{21}}$ ; $\frac{{25}}{{17}}$ ; $\frac{{13}}{{42}}$
- Các phân số chưa tối giản là: $\frac{2}{6}$ ; $\frac{{20}}{{35}}$ ; $\frac{{27}}{{57}}$
b) Rút gọn các phân số chưa tối giản:
$\frac{2}{6} = \frac{{2:2}}{{6:2}} = \frac{1}{3}$
$\frac{{20}}{{35}} = \frac{{20:5}}{{35:5}} = \frac{4}{7}$
$\frac{{27}}{{57}} = \frac{{27:3}}{{57:3}} = \frac{9}{{19}}$
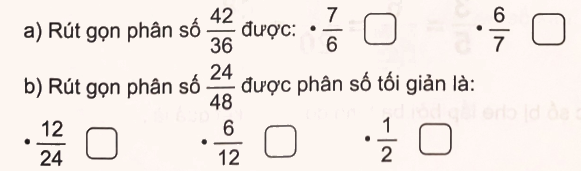
Đ, S ?
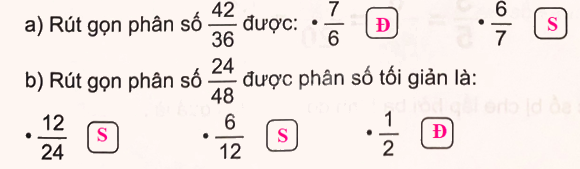
Phương pháp giải:
- Xét xem tử số và mẫu số cùng chia hết cho số tự nhiên nào lớn hơn 1.
- Chia tử số và mẫu số cho số đó.
Cứ làm như thế cho đến khi nhận được phân số tối giản (phân số không thể rút gọn được nữa).
Lời giải chi tiết:
a) Ta có: $\frac{{42}}{{36}} = \frac{{42:6}}{{36:6}} = \frac{7}{6}$
b) $\frac{{24}}{{48}} = \frac{{24:24}}{{48:24}} = \frac{1}{2}$
Vậy ta có kết quả sau:
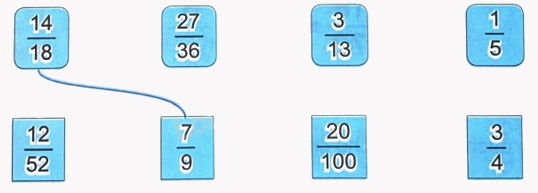
Nối hai phân số bằng nhau (theo mẫu).
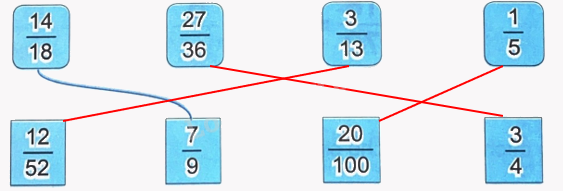
Phương pháp giải:
- Xét xem tử số và mẫu số cùng chia hết cho số tự nhiên nào lớn hơn 1.
- Chia tử số và mẫu số cho số đó.
Cứ làm như thế cho đến khi nhận được phân số tối giản (phân số không thể rút gọn được nữa).
Lời giải chi tiết:
Ta có: $\frac{{27}}{{36}} = \frac{{27:9}}{{36:9}} = \frac{3}{4}$
$\frac{{12}}{{52}} = \frac{{12:4}}{{52:4}} = \frac{3}{{13}}$
$\frac{{20}}{{100}} = \frac{{20:20}}{{100:20}} = \frac{1}{5}$
Vậy ta có kết quả sau:
Cho các phân số: $\frac{2}{6}$ ; $\frac{{19}}{{21}}$ ; $\frac{{25}}{{17}}$ ; $\frac{{13}}{{42}}$ ; $\frac{{20}}{{35}}$ ; $\frac{{27}}{{57}}$
a) Viết tiếp vào chỗ chấm cho thích hợp.
- Các phân số tối giản là: ………………………………..
- Các phân số chưa tối giản là: ……………………………………….
b) Rút gọn các phân số chưa tối giản ở câu a.
Phương pháp giải:
a)Phân số tối giản là phân số mà tử số và mẫu số không cùng chia hết cho số tự nhiên nào lớn hơn 1.
b) Cách rút gọn phân số:
- Xét xem tử số và mẫu số cùng chia hết cho số tự nhiên nào lớn hơn 1.
- Chia tử số và mẫu số cho số đó.
Cứ làm như thế cho đến khi nhận được phân số tối giản
Lời giải chi tiết:
a)
- Các phân số tối giản là: $\frac{{19}}{{21}}$ ; $\frac{{25}}{{17}}$ ; $\frac{{13}}{{42}}$
- Các phân số chưa tối giản là: $\frac{2}{6}$ ; $\frac{{20}}{{35}}$ ; $\frac{{27}}{{57}}$
b) Rút gọn các phân số chưa tối giản:
$\frac{2}{6} = \frac{{2:2}}{{6:2}} = \frac{1}{3}$
$\frac{{20}}{{35}} = \frac{{20:5}}{{35:5}} = \frac{4}{7}$
$\frac{{27}}{{57}} = \frac{{27:3}}{{57:3}} = \frac{9}{{19}}$
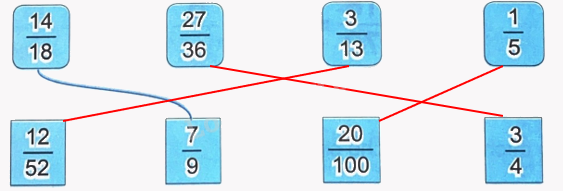
Nối hai phân số bằng nhau (theo mẫu).
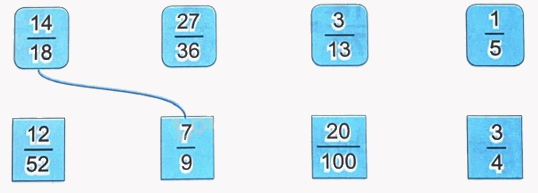
Phương pháp giải:
- Xét xem tử số và mẫu số cùng chia hết cho số tự nhiên nào lớn hơn 1.
- Chia tử số và mẫu số cho số đó.
Cứ làm như thế cho đến khi nhận được phân số tối giản (phân số không thể rút gọn được nữa).
Lời giải chi tiết:
Ta có: $\frac{{27}}{{36}} = \frac{{27:9}}{{36:9}} = \frac{3}{4}$
$\frac{{12}}{{52}} = \frac{{12:4}}{{52:4}} = \frac{3}{{13}}$
$\frac{{20}}{{100}} = \frac{{20:20}}{{100:20}} = \frac{1}{5}$
Vậy ta có kết quả sau:
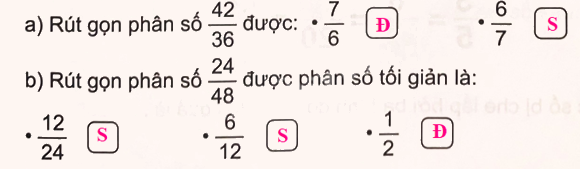
Đ, S ?
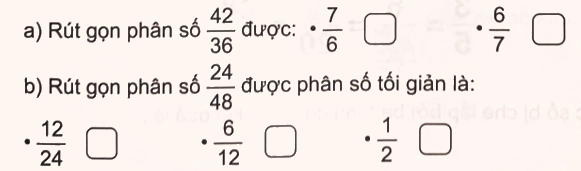
Phương pháp giải:
- Xét xem tử số và mẫu số cùng chia hết cho số tự nhiên nào lớn hơn 1.
- Chia tử số và mẫu số cho số đó.
Cứ làm như thế cho đến khi nhận được phân số tối giản (phân số không thể rút gọn được nữa).
Lời giải chi tiết:
a) Ta có: $\frac{{42}}{{36}} = \frac{{42:6}}{{36:6}} = \frac{7}{6}$
b) $\frac{{24}}{{48}} = \frac{{24:24}}{{48:24}} = \frac{1}{2}$
Vậy ta có kết quả sau:
Bài 56 trong Vở bài tập Toán 4 Kết nối tri thức với cuộc sống là một bước quan trọng trong việc củng cố kiến thức về phân số cho học sinh. Bài học này tập trung vào việc rèn luyện kỹ năng rút gọn phân số, một kỹ năng nền tảng cho các phép toán phức tạp hơn trong tương lai.
Mục tiêu chính của bài học này là giúp học sinh:
Để rút gọn phân số, chúng ta cần thực hiện các bước sau:
Ví dụ: Rút gọn phân số 12/18.
Bài 56 bao gồm các bài tập khác nhau, yêu cầu học sinh rút gọn các phân số khác nhau. Dưới đây là lời giải chi tiết cho từng bài tập:
a) 15/25: ƯCLN(15, 25) = 5. 15 : 5 = 3; 25 : 5 = 5. Vậy, 15/25 = 3/5.
b) 18/24: ƯCLN(18, 24) = 6. 18 : 6 = 3; 24 : 6 = 4. Vậy, 18/24 = 3/4.
c) 21/28: ƯCLN(21, 28) = 7. 21 : 7 = 3; 28 : 7 = 4. Vậy, 21/28 = 3/4.
d) 36/48: ƯCLN(36, 48) = 12. 36 : 12 = 3; 48 : 12 = 4. Vậy, 36/48 = 3/4.
a) 10/15 = 2/3 (Chia cả tử và mẫu cho 5)
b) 12/16 = 3/4 (Chia cả tử và mẫu cho 4)
Để củng cố kiến thức về rút gọn phân số, các em có thể tự giải thêm các bài tập sau:
Bài 56: Rút gọn phân số (tiết 1) trang 64 Vở bài tập Toán 4 - Kết nối tri thức với cuộc sống là một bài học quan trọng giúp học sinh nắm vững kỹ năng rút gọn phân số. Việc luyện tập thường xuyên sẽ giúp các em tự tin hơn trong việc giải các bài toán liên quan đến phân số.
Hy vọng với lời giải chi tiết và hướng dẫn cụ thể này, các em học sinh sẽ hiểu rõ hơn về bài học và đạt kết quả tốt trong môn Toán.