Bài 69 trong chương trình Toán 4 - Kết nối tri thức với cuộc sống là một bài ôn tập quan trọng về kiến thức phân số. Bài học này giúp học sinh củng cố lại các khái niệm cơ bản về phân số, các phép toán với phân số và ứng dụng của phân số trong thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho từng phần của bài tập, giúp học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Khoanh vào chữ đặt trước câu trả lời đúng. a) Phân số chỉ phần đã tô màu của hình bên là: Có ba vòi nước cùng chảy vào một bể. Trong 1 giờ, vòi số 1 chảy được 1/3 bể nước
Quy đồng mẫu số các phân số:
$\frac{3}{8}$ và $\frac{{19}}{{32}}$
$\frac{{37}}{{60}}$ và $\frac{{13}}{{15}}$
$\frac{5}{7}$ ; $\frac{8}{9}$ và $\frac{{48}}{{63}}$
Phương pháp giải:
- Xác định mẫu số chung
- Tìm thương của mẫu số chung và mẫu số của phân số kia.
- Lấy thương tìm được nhân với tử số và mẫu số của phân số cần quy đồng
Lời giải chi tiết:
+) $\frac{3}{8}$ và $\frac{{19}}{{32}}$
$\frac{3}{8} = \frac{{3 \times 4}}{{8 \times 4}} = \frac{{12}}{{32}}$
+) $\frac{{37}}{{60}}$ và $\frac{{13}}{{15}}$
$\frac{{13}}{{15}} = \frac{{13 \times 4}}{{15 \times 4}} = \frac{{52}}{{60}}$
+) $\frac{5}{7}$ ; $\frac{8}{9}$và $\frac{{48}}{{63}}$
$\frac{5}{7} = \frac{{5 \times 9}}{{7 \times 9}} = \frac{{45}}{{63}}$ ; $\frac{8}{9} = \frac{{8 \times 7}}{{9 \times 7}} = \frac{{56}}{{63}}$
Có ba vòi nước cùng chảy vào một bể. Trong 1 giờ, vòi số 1 chảy được $\frac{1}{3}$ bể nước, vòi số 2 chảy được $\frac{3}{8}$ bể nước, vòi số 3 chảy được $\frac{7}{{24}}$ bể nước. Hỏi trong 1 giờ, vòi nào chảy được nhiều nước nhất, vòi nào chảy được ít nước nhất?
Phương pháp giải:
So sánh phân số chỉ số phần nước chảy của ba vòi rồi kết luận
Lời giải chi tiết:
$\frac{1}{3} = \frac{{1 \times 8}}{{3 \times 8}} = \frac{8}{{24}}$; $\frac{3}{8} = \frac{{3 \times 3}}{{8 \times 3}} = \frac{9}{{24}}$
Ta có: $\frac{7}{{24}} < \frac{8}{{24}} < \frac{9}{{24}}$ nên $\frac{7}{{24}} < \frac{1}{3} < \frac{3}{8}$
Vậy trong 1 giờ vòi số 2 chảy được nhiều nước nhất, vòi số 3 chảy được ít nước nhất.
>; <; = ?
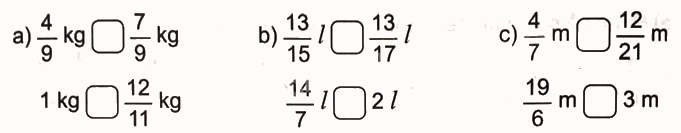
Phương pháp giải:
- Trong hai phân số cùng mẫu số: Phân số nào có tử số bé hơn thì bé hơn.
- Muốn so sánh hai phân số khác mẫu số, ta có thể quy đồng mẫu số hai phân số đó, rồi so sánh các tử số của hai phân số mới.
- Hai phân số có cùng tử số, phân số nào có mẫu số bé hơn thì phân số đó lớn hơn. - Nếu tử số lớn mẫu số thì phân số lớn hơn 1.
Lời giải chi tiết:
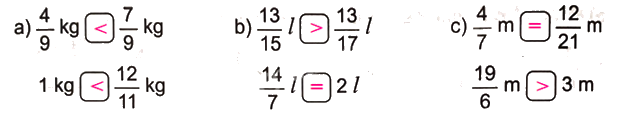
Số?
Phương pháp giải:
- Nếu nhân cả tử số và mẫu số của một phân số với cùng một số tự nhiên khác 0 thì được một phân số bằng phân số đã cho.
- Nếu chia cả tử số và mẫu số của một phân số cho cùng một số tự nhiên khác 0 thì được một phân số bằng phân số đã cho.
Lời giải chi tiết:
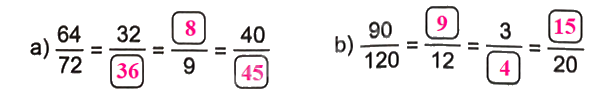
Khoanh vào chữ đặt trước câu trả lời đúng.
a) Phân số chỉ phần đã tô màu của hình bên là:
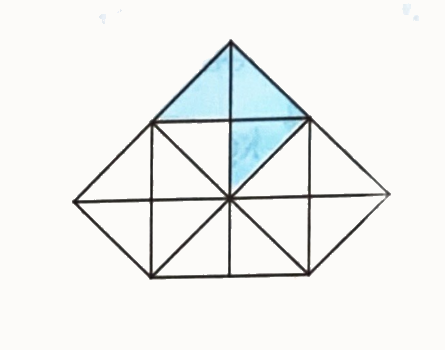
A. $\frac{3}{{11}}$
B. $\frac{{11}}{{14}}$
C.$\frac{3}{{14}}$
D.$\frac{{11}}{3}$
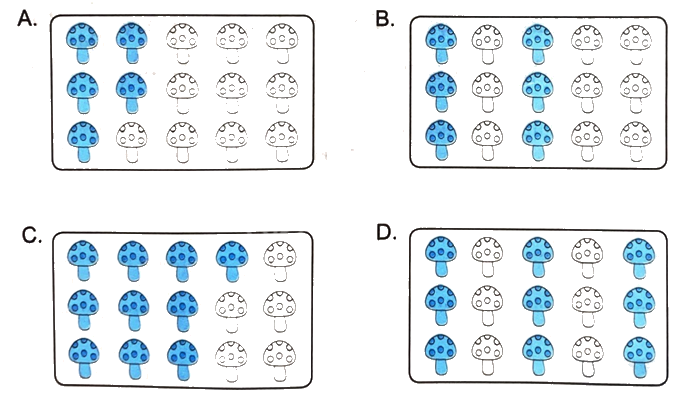
b) Đã tô màu $\frac{2}{5}$ số cây nấm của hình nào dưới đây?
Phương pháp giải:
a) Phân số chỉ phần đã tô màu có tử số là số phần đã tô màu, mẫu số là số phần bằng nhau.
b) Quan sát hình vẽ rồi chọn đáp án thích hợp
Lời giải chi tiết:
a) Hình vẽ gồm 14 phần bằng nhau, có 3 phần được tô màu. Vậy phân số chỉ số phần đã tô màu là $\frac{3}{{14}}$.
ChọnC b) Ta thấy, hình B các cây nấm được xếp thành 5 hàng dọc, mỗi hàng đều có 3 cây nấm.
Có 2 hàng nấm được tô màu.
Vậy đã tô màu $\frac{2}{5}$ số cây nấm của hình B
Chọn B
Khoanh vào chữ đặt trước câu trả lời đúng.
a) Phân số chỉ phần đã tô màu của hình bên là:
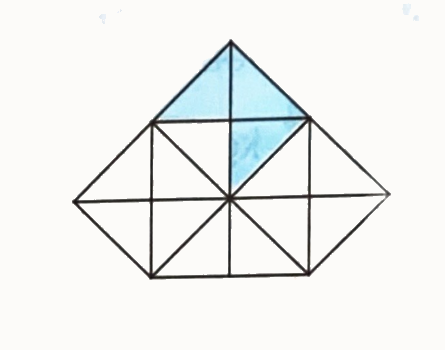
A. $\frac{3}{{11}}$
B. $\frac{{11}}{{14}}$
C.$\frac{3}{{14}}$
D.$\frac{{11}}{3}$
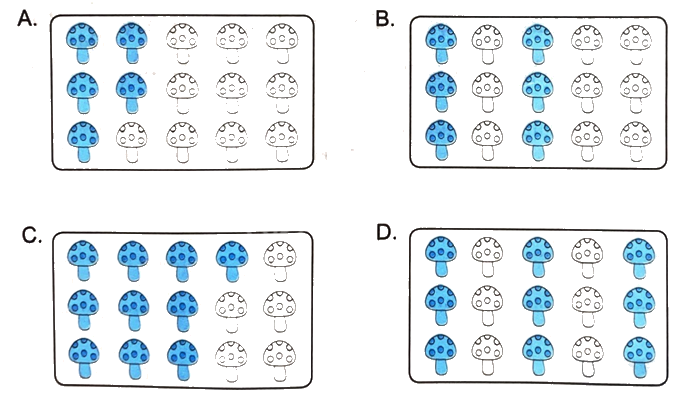
b) Đã tô màu $\frac{2}{5}$ số cây nấm của hình nào dưới đây?
Phương pháp giải:
a) Phân số chỉ phần đã tô màu có tử số là số phần đã tô màu, mẫu số là số phần bằng nhau.
b) Quan sát hình vẽ rồi chọn đáp án thích hợp
Lời giải chi tiết:
a) Hình vẽ gồm 14 phần bằng nhau, có 3 phần được tô màu. Vậy phân số chỉ số phần đã tô màu là $\frac{3}{{14}}$.
ChọnC b) Ta thấy, hình B các cây nấm được xếp thành 5 hàng dọc, mỗi hàng đều có 3 cây nấm.
Có 2 hàng nấm được tô màu.
Vậy đã tô màu $\frac{2}{5}$ số cây nấm của hình B
Chọn B
Số?
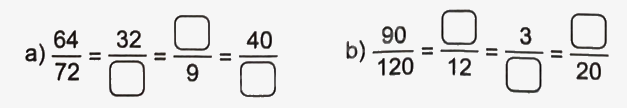
Phương pháp giải:
- Nếu nhân cả tử số và mẫu số của một phân số với cùng một số tự nhiên khác 0 thì được một phân số bằng phân số đã cho.
- Nếu chia cả tử số và mẫu số của một phân số cho cùng một số tự nhiên khác 0 thì được một phân số bằng phân số đã cho.
Lời giải chi tiết:
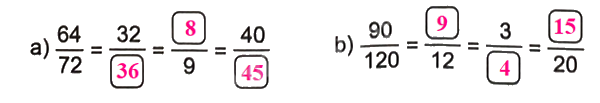
Quy đồng mẫu số các phân số:
$\frac{3}{8}$ và $\frac{{19}}{{32}}$
$\frac{{37}}{{60}}$ và $\frac{{13}}{{15}}$
$\frac{5}{7}$ ; $\frac{8}{9}$ và $\frac{{48}}{{63}}$
Phương pháp giải:
- Xác định mẫu số chung
- Tìm thương của mẫu số chung và mẫu số của phân số kia.
- Lấy thương tìm được nhân với tử số và mẫu số của phân số cần quy đồng
Lời giải chi tiết:
+) $\frac{3}{8}$ và $\frac{{19}}{{32}}$
$\frac{3}{8} = \frac{{3 \times 4}}{{8 \times 4}} = \frac{{12}}{{32}}$
+) $\frac{{37}}{{60}}$ và $\frac{{13}}{{15}}$
$\frac{{13}}{{15}} = \frac{{13 \times 4}}{{15 \times 4}} = \frac{{52}}{{60}}$
+) $\frac{5}{7}$ ; $\frac{8}{9}$và $\frac{{48}}{{63}}$
$\frac{5}{7} = \frac{{5 \times 9}}{{7 \times 9}} = \frac{{45}}{{63}}$ ; $\frac{8}{9} = \frac{{8 \times 7}}{{9 \times 7}} = \frac{{56}}{{63}}$
>; <; = ?
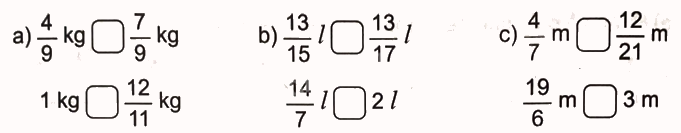
Phương pháp giải:
- Trong hai phân số cùng mẫu số: Phân số nào có tử số bé hơn thì bé hơn.
- Muốn so sánh hai phân số khác mẫu số, ta có thể quy đồng mẫu số hai phân số đó, rồi so sánh các tử số của hai phân số mới.
- Hai phân số có cùng tử số, phân số nào có mẫu số bé hơn thì phân số đó lớn hơn. - Nếu tử số lớn mẫu số thì phân số lớn hơn 1.
Lời giải chi tiết:
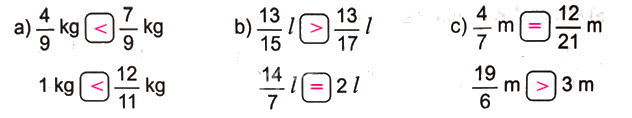
Có ba vòi nước cùng chảy vào một bể. Trong 1 giờ, vòi số 1 chảy được $\frac{1}{3}$ bể nước, vòi số 2 chảy được $\frac{3}{8}$ bể nước, vòi số 3 chảy được $\frac{7}{{24}}$ bể nước. Hỏi trong 1 giờ, vòi nào chảy được nhiều nước nhất, vòi nào chảy được ít nước nhất?
Phương pháp giải:
So sánh phân số chỉ số phần nước chảy của ba vòi rồi kết luận
Lời giải chi tiết:
$\frac{1}{3} = \frac{{1 \times 8}}{{3 \times 8}} = \frac{8}{{24}}$; $\frac{3}{8} = \frac{{3 \times 3}}{{8 \times 3}} = \frac{9}{{24}}$
Ta có: $\frac{7}{{24}} < \frac{8}{{24}} < \frac{9}{{24}}$ nên $\frac{7}{{24}} < \frac{1}{3} < \frac{3}{8}$
Vậy trong 1 giờ vòi số 2 chảy được nhiều nước nhất, vòi số 3 chảy được ít nước nhất.
Bài 69 trong Vở bài tập Toán 4 - Kết nối tri thức với cuộc sống là một bài ôn tập quan trọng, tổng hợp lại các kiến thức về phân số mà các em đã học. Để giúp các em học sinh hiểu rõ hơn và tự tin giải bài tập, giaitoan.edu.vn xin trình bày lời giải chi tiết cho từng phần của bài tập này.
Bài 69 yêu cầu học sinh thực hiện các nhiệm vụ sau:
Câu 1: Viết phân số biểu diễn phần đã tô màu trong mỗi hình.
Để viết phân số biểu diễn phần đã tô màu, các em cần xác định số phần đã tô màu và tổng số phần bằng nhau của hình. Ví dụ, nếu một hình tròn được chia thành 4 phần bằng nhau và có 1 phần được tô màu, thì phân số biểu diễn phần đã tô màu là 1/4.
Câu 2: Đọc các phân số đã cho.
Để đọc phân số, các em đọc tử số trước, sau đó đọc “phần” và cuối cùng đọc mẫu số. Ví dụ, phân số 1/4 được đọc là “một phần tư”.
Câu 3: Phân số nào chỉ phần đã tô màu?
Để chọn phân số chỉ phần đã tô màu, các em cần so sánh phân số với hình ảnh đã cho. Phân số nào biểu diễn đúng số phần đã tô màu và tổng số phần bằng nhau thì đó là đáp án đúng.
Câu 4: So sánh phân số.
Để so sánh phân số, các em có thể sử dụng các phương pháp sau:
Câu 5: Bài toán có lời văn.
Để giải bài toán có lời văn, các em cần:
Khi học bài 69, các em cần lưu ý những điều sau:
Giaitoan.edu.vn hy vọng với lời giải chi tiết này, các em học sinh sẽ hiểu rõ hơn về bài 69 và tự tin giải các bài tập tương tự. Chúc các em học tốt!