Bài 61 thuộc chương trình Toán 4 Kết nối tri thức với cuộc sống, tập trung vào việc củng cố kỹ năng phép trừ phân số. Bài học này giúp học sinh hiểu rõ hơn về cách thực hiện phép trừ với các phân số khác nhau, từ đó nâng cao khả năng giải quyết các bài toán thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp các em học sinh tự tin chinh phục bài học này.
Tính 2/3 - 1/6 .... Rút gọn rồi tính 14/16 - 3/8
Tính.
a) $\frac{2}{3} - \frac{1}{6}$
b) $\frac{4}{6} - \frac{5}{{12}}$
c) $\frac{7}{{15}} - \frac{2}{5}$
d) $\frac{{19}}{{12}} - \frac{5}{4}$
Phương pháp giải:
Muốn trừ hai phân số khác mẫu số, ta quy đồng mẫu số hai phân số, rồi trừ hai phân số đó.
Lời giải chi tiết:
a) $\frac{2}{3} - \frac{1}{6} = \frac{4}{6} - \frac{1}{6} = \frac{3}{6} = \frac{1}{2}$
b) $\frac{4}{6} - \frac{5}{{12}} = \frac{8}{{12}} - \frac{5}{{12}} = \frac{3}{{12}} = \frac{1}{4}$
c) $\frac{7}{{15}} - \frac{2}{5} = \frac{7}{{15}} - \frac{6}{{15}} = \frac{1}{{15}}$
d) $\frac{{19}}{{12}} - \frac{5}{4} = \frac{{19}}{{12}} - \frac{{15}}{{12}} = \frac{4}{{12}} = \frac{1}{3}$
Rút gọn rồi tính.
a) $\frac{{14}}{{16}} - \frac{3}{8}$
b) $\frac{6}{{10}} - \frac{1}{5}$
c) $\frac{5}{7} - \frac{6}{{21}}$
d) $\frac{6}{9} - \frac{1}{3}$
Phương pháp giải:
- Rút gọn các phân số chưa tối giản
- Muốn trừ hai phân số khác mẫu số, ta quy đồng mẫu số hai phân số, rồi trừ hai phân số đó.
Lời giải chi tiết:
a) $\frac{{14}}{{16}} - \frac{3}{8} = \frac{7}{8} - \frac{3}{8} = \frac{4}{8} = \frac{1}{2}$
b) $\frac{6}{{10}} - \frac{1}{5} = \frac{3}{5} - \frac{1}{5} = \frac{2}{5}$
c) $\frac{5}{7} - \frac{6}{{21}} = \frac{5}{7} - \frac{2}{7} = \frac{3}{7}$
d) $\frac{6}{9} - \frac{1}{3} = \frac{2}{3} - \frac{1}{3} = \frac{1}{3}$
Ca thứ nhất có $\frac{4}{9}$ $\ell $ nước. Ca thứ hai có $\frac{5}{{18}}$ $\ell $ nước. Bạn Mai rót hết nước từ hai ca đó vào một chiếc bình.
a) Tính lượng nước có trong bình.
b) Sau đó, Mai lấy $\frac{1}{2}$ $\ell $ nước từ trong chiếc bình đó. Tính lượng nước còn lại trong bình.
Phương pháp giải:
a) Lượng nước có trong bình = lượng nước ca thứ nhất + lượng nước ca thứ hai
b) Lượng nước còn lại trong bình = lượng nước có trong bình – lượng nước lấy ra
Lời giải chi tiết:
a) Lượng nước có trong bình là:
$\frac{4}{9} + \frac{5}{{18}} = \frac{{13}}{{18}}$ (lít)
b) Lượng nước còn lại trong bình là:
$\frac{{13}}{{18}} - \frac{1}{2} = \frac{2}{9}$ (lít)
Đáp số: a) $\frac{{13}}{{18}}\,l$ nước
b) $\frac{2}{9}\,l$ nước
Trong hai bình A và B, bình nào đang chứa nhiều nước hơn và nhiều hơn bao nhiêu lít nước?
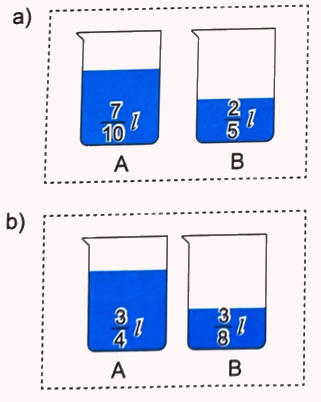
Phương pháp giải:
So sánh các phân số ghi trên hai bình rồi kết luận
Lời giải chi tiết:
a) Ta có: $\frac{2}{5} = \frac{4}{{10}}$
Mà $\frac{7}{{10}} > \frac{4}{{10}}$ nên $\frac{7}{{10}} > \frac{2}{5}$
Vậy bình A chứa nhiều nước hơn.
Bình A chứa nhiều hơn bình B số lít nước là: $\frac{7}{{10}} - \frac{2}{5} = \frac{3}{{10}}$ (lít)
b) Ta có: $\frac{3}{4} = \frac{6}{8}$
Mà $\frac{6}{8} > \frac{3}{8}$ nên $\frac{3}{4} > \frac{3}{8}$
Vậy bình A chứa nhiều nước hơn.
Bình A chứa nhiều hơn bình B số lít nước là: $\frac{3}{4} - \frac{3}{8} = \frac{3}{8}$
Nối (theo mẫu).
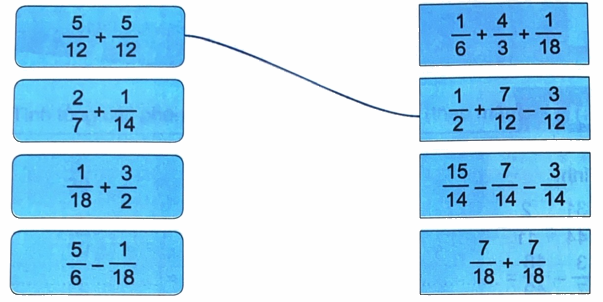
Phương pháp giải:
Tính rồi nối các biểu thức có kết quả bằng nhau.
Lời giải chi tiết:
$\frac{2}{7} + \frac{1}{{14}} = \frac{4}{{14}} + \frac{1}{{14}} = \frac{5}{{14}}$
$\frac{1}{{18}} + \frac{3}{2} = \frac{1}{{18}} + \frac{{27}}{{18}} = \frac{{28}}{{18}}$
$\frac{5}{6} - \frac{1}{{18}} = \frac{{15}}{{18}} - \frac{1}{{18}} = \frac{{14}}{{18}}$
$\frac{1}{6} + \frac{4}{3} + \frac{1}{{18}} = \frac{3}{{18}} + \frac{{24}}{{18}} + \frac{1}{{18}} = \frac{{28}}{{18}}$
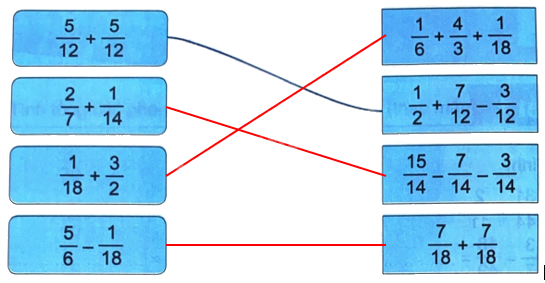
$\frac{{15}}{{14}} - \frac{7}{{14}} - \frac{3}{{14}} = \frac{{15 - 7 - 3}}{{14}} = \frac{5}{{14}}$
$\frac{7}{{18}} + \frac{7}{{18}} = \frac{{14}}{{18}}$
Tính.
a) $\frac{2}{3} - \frac{1}{6}$
b) $\frac{4}{6} - \frac{5}{{12}}$
c) $\frac{7}{{15}} - \frac{2}{5}$
d) $\frac{{19}}{{12}} - \frac{5}{4}$
Phương pháp giải:
Muốn trừ hai phân số khác mẫu số, ta quy đồng mẫu số hai phân số, rồi trừ hai phân số đó.
Lời giải chi tiết:
a) $\frac{2}{3} - \frac{1}{6} = \frac{4}{6} - \frac{1}{6} = \frac{3}{6} = \frac{1}{2}$
b) $\frac{4}{6} - \frac{5}{{12}} = \frac{8}{{12}} - \frac{5}{{12}} = \frac{3}{{12}} = \frac{1}{4}$
c) $\frac{7}{{15}} - \frac{2}{5} = \frac{7}{{15}} - \frac{6}{{15}} = \frac{1}{{15}}$
d) $\frac{{19}}{{12}} - \frac{5}{4} = \frac{{19}}{{12}} - \frac{{15}}{{12}} = \frac{4}{{12}} = \frac{1}{3}$
Rút gọn rồi tính.
a) $\frac{{14}}{{16}} - \frac{3}{8}$
b) $\frac{6}{{10}} - \frac{1}{5}$
c) $\frac{5}{7} - \frac{6}{{21}}$
d) $\frac{6}{9} - \frac{1}{3}$
Phương pháp giải:
- Rút gọn các phân số chưa tối giản
- Muốn trừ hai phân số khác mẫu số, ta quy đồng mẫu số hai phân số, rồi trừ hai phân số đó.
Lời giải chi tiết:
a) $\frac{{14}}{{16}} - \frac{3}{8} = \frac{7}{8} - \frac{3}{8} = \frac{4}{8} = \frac{1}{2}$
b) $\frac{6}{{10}} - \frac{1}{5} = \frac{3}{5} - \frac{1}{5} = \frac{2}{5}$
c) $\frac{5}{7} - \frac{6}{{21}} = \frac{5}{7} - \frac{2}{7} = \frac{3}{7}$
d) $\frac{6}{9} - \frac{1}{3} = \frac{2}{3} - \frac{1}{3} = \frac{1}{3}$
Trong hai bình A và B, bình nào đang chứa nhiều nước hơn và nhiều hơn bao nhiêu lít nước?
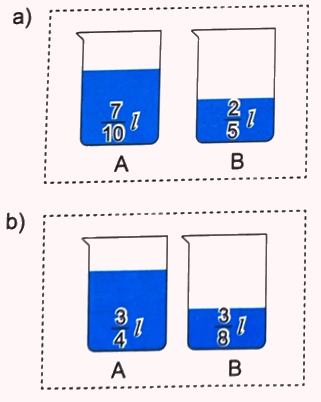
Phương pháp giải:
So sánh các phân số ghi trên hai bình rồi kết luận
Lời giải chi tiết:
a) Ta có: $\frac{2}{5} = \frac{4}{{10}}$
Mà $\frac{7}{{10}} > \frac{4}{{10}}$ nên $\frac{7}{{10}} > \frac{2}{5}$
Vậy bình A chứa nhiều nước hơn.
Bình A chứa nhiều hơn bình B số lít nước là: $\frac{7}{{10}} - \frac{2}{5} = \frac{3}{{10}}$ (lít)
b) Ta có: $\frac{3}{4} = \frac{6}{8}$
Mà $\frac{6}{8} > \frac{3}{8}$ nên $\frac{3}{4} > \frac{3}{8}$
Vậy bình A chứa nhiều nước hơn.
Bình A chứa nhiều hơn bình B số lít nước là: $\frac{3}{4} - \frac{3}{8} = \frac{3}{8}$
Nối (theo mẫu).
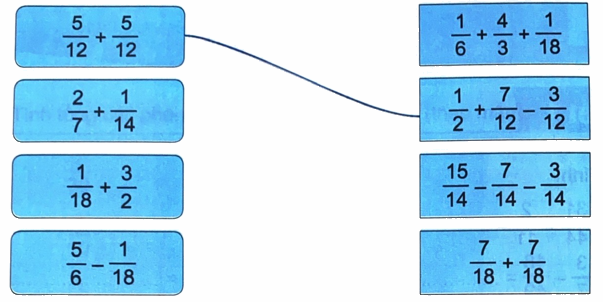
Phương pháp giải:
Tính rồi nối các biểu thức có kết quả bằng nhau.
Lời giải chi tiết:
$\frac{2}{7} + \frac{1}{{14}} = \frac{4}{{14}} + \frac{1}{{14}} = \frac{5}{{14}}$
$\frac{1}{{18}} + \frac{3}{2} = \frac{1}{{18}} + \frac{{27}}{{18}} = \frac{{28}}{{18}}$
$\frac{5}{6} - \frac{1}{{18}} = \frac{{15}}{{18}} - \frac{1}{{18}} = \frac{{14}}{{18}}$
$\frac{1}{6} + \frac{4}{3} + \frac{1}{{18}} = \frac{3}{{18}} + \frac{{24}}{{18}} + \frac{1}{{18}} = \frac{{28}}{{18}}$
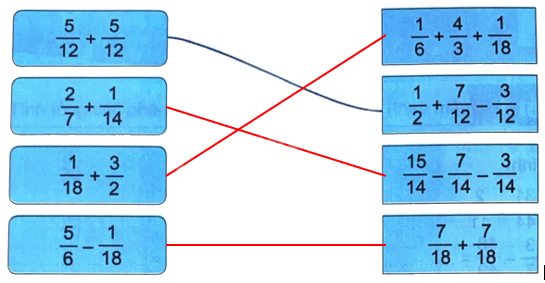
$\frac{{15}}{{14}} - \frac{7}{{14}} - \frac{3}{{14}} = \frac{{15 - 7 - 3}}{{14}} = \frac{5}{{14}}$
$\frac{7}{{18}} + \frac{7}{{18}} = \frac{{14}}{{18}}$
Ca thứ nhất có $\frac{4}{9}$ $\ell $ nước. Ca thứ hai có $\frac{5}{{18}}$ $\ell $ nước. Bạn Mai rót hết nước từ hai ca đó vào một chiếc bình.
a) Tính lượng nước có trong bình.
b) Sau đó, Mai lấy $\frac{1}{2}$ $\ell $ nước từ trong chiếc bình đó. Tính lượng nước còn lại trong bình.
Phương pháp giải:
a) Lượng nước có trong bình = lượng nước ca thứ nhất + lượng nước ca thứ hai
b) Lượng nước còn lại trong bình = lượng nước có trong bình – lượng nước lấy ra
Lời giải chi tiết:
a) Lượng nước có trong bình là:
$\frac{4}{9} + \frac{5}{{18}} = \frac{{13}}{{18}}$ (lít)
b) Lượng nước còn lại trong bình là:
$\frac{{13}}{{18}} - \frac{1}{2} = \frac{2}{9}$ (lít)
Đáp số: a) $\frac{{13}}{{18}}\,l$ nước
b) $\frac{2}{9}\,l$ nước
Bài 61 trong Vở bài tập Toán 4 Kết nối tri thức với cuộc sống là một bước quan trọng trong việc giúp học sinh nắm vững kiến thức về phép trừ phân số. Bài học này không chỉ giới thiệu cách thực hiện phép trừ phân số cơ bản mà còn đi sâu vào các trường hợp phức tạp hơn, đòi hỏi học sinh phải vận dụng linh hoạt các kiến thức đã học.
Trước khi đi vào giải bài tập, chúng ta cùng ôn lại một số kiến thức cơ bản về phép trừ phân số:
Bài 61 thường bao gồm các dạng bài tập sau:
Ví dụ: 5/7 - 2/7 = (5-2)/7 = 3/7
Để giải dạng bài này, học sinh cần thực hiện theo các bước sau:
Ví dụ: 1/2 - 1/3
Để giải dạng bài này, học sinh cần thực hiện theo các bước sau:
Trong trường hợp bài toán yêu cầu tìm phân số trung bình của hai phân số, ta có thể sử dụng công thức: (a/b + c/d) / 2
Các bài toán ứng dụng thường yêu cầu học sinh vận dụng kiến thức về phép trừ phân số để giải quyết các tình huống thực tế. Ví dụ: Một người có 3/4 chiếc bánh, người đó ăn 1/4 chiếc bánh. Hỏi người đó còn lại bao nhiêu chiếc bánh?
Để giải dạng bài này, học sinh cần:
Để củng cố kiến thức về phép trừ phân số, học sinh có thể luyện tập thêm với các bài tập sau:
Khi giải bài tập về phép trừ phân số, học sinh cần lưu ý những điều sau:
Hy vọng với những hướng dẫn chi tiết trên, các em học sinh sẽ tự tin giải bài 61: Phép trừ phân số (tiết 3) trang 82 Vở bài tập Toán 4 - Kết nối tri thức với cuộc sống một cách hiệu quả. Chúc các em học tốt!