Bài 58 thuộc chương trình Toán 4 Kết nối tri thức với cuộc sống, tập trung vào việc rèn luyện kỹ năng so sánh phân số. Bài học này giúp học sinh nắm vững các phương pháp so sánh phân số khác nhau, từ đó áp dụng vào giải quyết các bài toán thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho bài 58, giúp các em học sinh tự tin hơn trong việc học Toán.
So sánh hai phân số chỉ số phần đã tô màu của mỗi hình.
Sắp xếp các phân số $\frac{{19}}{{23}}$; $\frac{{13}}{{23}}$ ; $\frac{{39}}{{23}}$; $\frac{7}{{23}}$
a) Theo thứ tự từ bé đến lớn: ……………………………………………….
b) Theo thứ tự từ lớn đến bé: …………………………………………………
Phương pháp giải:
So sánh rồi sắp xếp các phân số theo yêu cầu đề bài.
Lời giải chi tiết:
Ta có: $\frac{7}{{23}} < \frac{{13}}{{23}} < \frac{{19}}{{23}} < \frac{{39}}{{23}}$
a) Các phân số sắp xếp theo thứ tự từ bé đến lớn: $\frac{7}{{23}}$; $\frac{{13}}{{23}}$ ; $\frac{{19}}{{23}}$ ; $\frac{{39}}{{23}}$
b) Các phân số sắp xếp theo thứ tự từ lớn đến bé: $\frac{{39}}{{23}}$ ; $\frac{{19}}{{23}}$ ; $\frac{{13}}{{23}}$ ; $\frac{7}{{23}}$
Khoanh vào chữ đặt trước câu trả lời đúng.
Trong các phân số $\frac{{15}}{{16}}$, $\frac{{31}}{{30}}$ ; $\frac{{99}}{{100}}$ ; $\frac{{47}}{{48}}$ phân số lớn nhất là:
A. $\frac{{15}}{{16}}$
B. $\frac{{31}}{{30}}$
C.$\frac{{99}}{{100}}$
D. $\frac{{47}}{{48}}$
Phương pháp giải:
- Nếu tử số bé hơn mẫu số thì phân số bé hơn 1.
- Nếu tử số lớn mẫu số thì phân số lớn hơn 1.
- Nếu tử số bằng mẫu số thì phân số bằng 1.
Lời giải chi tiết:
Ta có: $\frac{{15}}{{16}} < 1$ ; $\frac{{31}}{{30}} > 1$ ; $\frac{{99}}{{100}} < 1$ ; $\frac{{47}}{{48}} < 1$
Vậy phân số lớn nhất là $\frac{{31}}{{30}}$
Chọn B
>; <; = ?
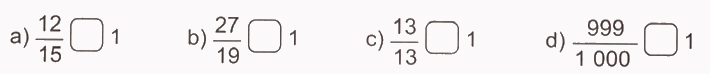
Phương pháp giải:
- Nếu tử số bé hơn mẫu số thì phân số bé hơn 1.
- Nếu tử số lớn mẫu số thì phân số lớn hơn 1.
- Nếu tử số bằng mẫu số thì phân số bằng 1.
Lời giải chi tiết:

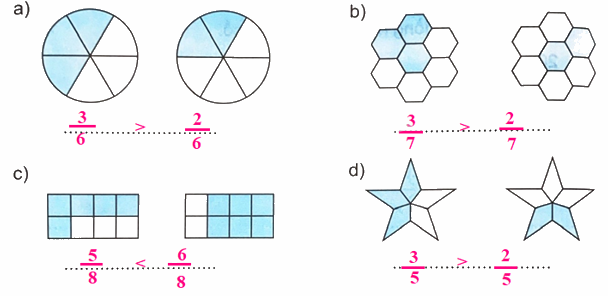
So sánh hai phân số chỉ số phần đã tô màu của mỗi hình.
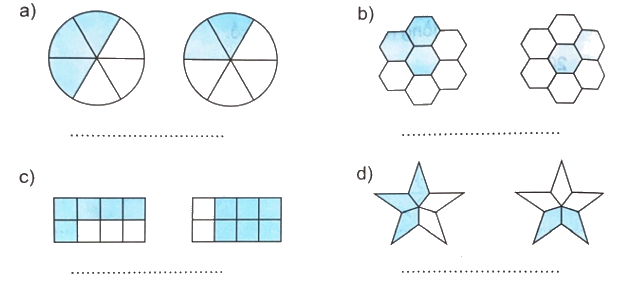
Phương pháp giải:
- Xác định phân số chỉ số phần được tô màu của mỗi hình
- So sánh hai phân số cùng mẫu số:
• Phân số nào có tử số bé hơn thì bé hơn.
• Phân số nào có tử số lớn hơn thì lớn hơn.
• Nếu hai tử số bằng nhau thì hai phân số đó bằng nhau.
Lời giải chi tiết:
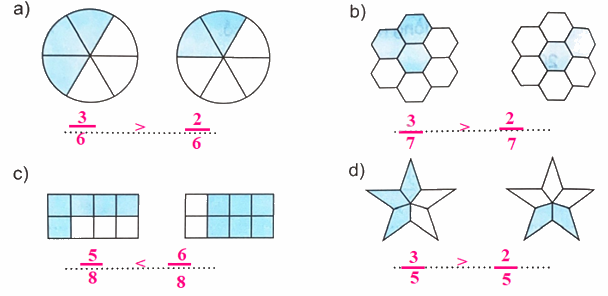
So sánh hai phân số chỉ số phần đã tô màu của mỗi hình.
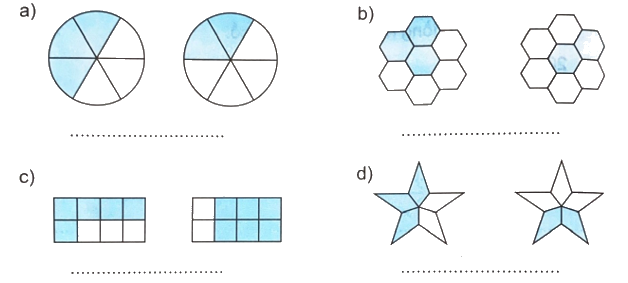
Phương pháp giải:
- Xác định phân số chỉ số phần được tô màu của mỗi hình
- So sánh hai phân số cùng mẫu số:
• Phân số nào có tử số bé hơn thì bé hơn.
• Phân số nào có tử số lớn hơn thì lớn hơn.
• Nếu hai tử số bằng nhau thì hai phân số đó bằng nhau.
Lời giải chi tiết:
>; <; = ?
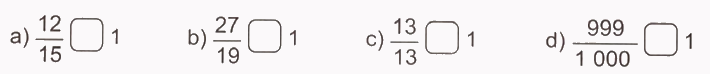
Phương pháp giải:
- Nếu tử số bé hơn mẫu số thì phân số bé hơn 1.
- Nếu tử số lớn mẫu số thì phân số lớn hơn 1.
- Nếu tử số bằng mẫu số thì phân số bằng 1.
Lời giải chi tiết:

Sắp xếp các phân số $\frac{{19}}{{23}}$; $\frac{{13}}{{23}}$ ; $\frac{{39}}{{23}}$; $\frac{7}{{23}}$
a) Theo thứ tự từ bé đến lớn: ……………………………………………….
b) Theo thứ tự từ lớn đến bé: …………………………………………………
Phương pháp giải:
So sánh rồi sắp xếp các phân số theo yêu cầu đề bài.
Lời giải chi tiết:
Ta có: $\frac{7}{{23}} < \frac{{13}}{{23}} < \frac{{19}}{{23}} < \frac{{39}}{{23}}$
a) Các phân số sắp xếp theo thứ tự từ bé đến lớn: $\frac{7}{{23}}$; $\frac{{13}}{{23}}$ ; $\frac{{19}}{{23}}$ ; $\frac{{39}}{{23}}$
b) Các phân số sắp xếp theo thứ tự từ lớn đến bé: $\frac{{39}}{{23}}$ ; $\frac{{19}}{{23}}$ ; $\frac{{13}}{{23}}$ ; $\frac{7}{{23}}$
Khoanh vào chữ đặt trước câu trả lời đúng.
Trong các phân số $\frac{{15}}{{16}}$, $\frac{{31}}{{30}}$ ; $\frac{{99}}{{100}}$ ; $\frac{{47}}{{48}}$ phân số lớn nhất là:
A. $\frac{{15}}{{16}}$
B. $\frac{{31}}{{30}}$
C.$\frac{{99}}{{100}}$
D. $\frac{{47}}{{48}}$
Phương pháp giải:
- Nếu tử số bé hơn mẫu số thì phân số bé hơn 1.
- Nếu tử số lớn mẫu số thì phân số lớn hơn 1.
- Nếu tử số bằng mẫu số thì phân số bằng 1.
Lời giải chi tiết:
Ta có: $\frac{{15}}{{16}} < 1$ ; $\frac{{31}}{{30}} > 1$ ; $\frac{{99}}{{100}} < 1$ ; $\frac{{47}}{{48}} < 1$
Vậy phân số lớn nhất là $\frac{{31}}{{30}}$
Chọn B
Bài 58 trong Vở bài tập Toán 4 Kết nối tri thức với cuộc sống là một bài tập quan trọng giúp học sinh củng cố kiến thức về so sánh phân số. Việc nắm vững phương pháp so sánh phân số là nền tảng để học sinh giải quyết các bài toán phức tạp hơn trong chương trình Toán học.
Mục tiêu chính của bài học này là giúp học sinh:
Bài 58 bao gồm các dạng bài tập sau:
Có nhiều phương pháp để so sánh phân số, tùy thuộc vào từng dạng bài tập cụ thể. Dưới đây là một số phương pháp phổ biến:
Khi hai phân số có cùng mẫu số, ta so sánh tử số của chúng. Phân số nào có tử số lớn hơn thì phân số đó lớn hơn.
Ví dụ: 3/5 > 2/5 vì 3 > 2.
Khi hai phân số có cùng tử số, ta so sánh mẫu số của chúng. Phân số nào có mẫu số nhỏ hơn thì phân số đó lớn hơn.
Ví dụ: 2/3 > 2/5 vì 3 < 5.
Để so sánh hai phân số khác mẫu số, ta quy đồng mẫu số của chúng. Sau đó, ta so sánh hai phân số mới có cùng mẫu số theo phương pháp so sánh hai phân số có cùng mẫu số.
Ví dụ: So sánh 1/2 và 2/3.
Quy đồng mẫu số: 1/2 = 3/6 và 2/3 = 4/6.
So sánh: 3/6 < 4/6, vậy 1/2 < 2/3.
Nếu một phân số có tử số lớn hơn mẫu số thì phân số đó lớn hơn 1. Nếu một phân số có tử số nhỏ hơn mẫu số thì phân số đó nhỏ hơn 1. Nếu một phân số có tử số bằng mẫu số thì phân số đó bằng 1.
Ví dụ: 5/4 > 1, 2/3 < 1, 3/3 = 1.
Để nắm vững kiến thức về so sánh phân số, các em học sinh cần luyện tập thường xuyên với các bài tập khác nhau. Các em có thể tìm thấy nhiều bài tập luyện tập trong sách giáo khoa, vở bài tập và trên các trang web học Toán online.
Bài tập 1: So sánh 4/7 và 5/7.
Lời giải: Vì hai phân số có cùng mẫu số, ta so sánh tử số: 4 < 5. Vậy 4/7 < 5/7.
Bài tập 2: So sánh 2/5 và 3/5.
Lời giải: Vì hai phân số có cùng mẫu số, ta so sánh tử số: 2 < 3. Vậy 2/5 < 3/5.
Bài tập 3: So sánh 1/3 và 1/4.
Lời giải: Vì hai phân số có cùng tử số, ta so sánh mẫu số: 3 < 4. Vậy 1/3 > 1/4.
Bài 58: So sánh phân số (tiết 1) trang 68 Vở bài tập Toán 4 - Kết nối tri thức với cuộc sống là một bài học quan trọng giúp học sinh nắm vững kiến thức cơ bản về so sánh phân số. Việc luyện tập thường xuyên và áp dụng các phương pháp so sánh phù hợp sẽ giúp các em học sinh tự tin hơn trong việc giải quyết các bài toán liên quan đến phân số.