Chào mừng bạn đến với Đề số 10 - Đề thi vào lớp 10 môn Toán tại giaitoan.edu.vn. Đây là một trong những đề thi thử quan trọng giúp bạn làm quen với cấu trúc đề thi và rèn luyện kỹ năng giải toán.
Đề thi này được thiết kế dựa trên cấu trúc đề thi tuyển sinh vào lớp 10 của các trường THPT trên cả nước, bao gồm các dạng bài tập khác nhau, từ trắc nghiệm đến tự luận, giúp bạn đánh giá năng lực một cách toàn diện.
Hãy cùng giaitoan.edu.vn chinh phục Đề số 10 này và tự tin bước vào kỳ thi tuyển sinh sắp tới!
Đề thi vào lớp 10 môn Toán - Đề số 10 có đáp án và lời giải chi tiết
Đề bài
Câu 1 (4 điểm) Tính giá trị của các biểu thức sau:
\(\begin{array}{l}a)\;A = \sqrt {16 + 9} - 2\\b)\;B = \sqrt {{{\left( {\sqrt 3 - 1} \right)}^2}} + 1\end{array}\)
Câu 2 (1,5 điểm)
Cho biểu thức \(P = \left( {\frac{{x - 6}}{{x + 3\sqrt x }} - \frac{1}{{\sqrt x }} + \frac{1}{{\sqrt x + 3}}} \right):\frac{{2\sqrt x - 6}}{{x + 1}}\) với \(x > 0,\;\;x \ne 9.\)
a) Rút gọn biểu thức P.
b) Tìm giá trị của x để \(P = 1.\)
Câu 3 (2,5 điểm)
1) Cho đường thẳng \(\left( d \right):\;\;y = - \dfrac{1}{2}x + 2.\)
a) Tìm \(m\) để đường thẳng \(\left( \Delta \right):\;y = \left( {m - 1} \right)x + 1\) song song với đường thẳng \(\left( d \right).\)
b) Gọi \(A,\;B\) là giao điểm của \(\left( d \right)\) với parabol \(\left( P \right):\;\;y = \dfrac{1}{4}{x^2}.\) Tìm tọa độ điểm \(N\) nằm trên trục hoành sao cho \(NA + NB\) nhỏ nhất.
2) Cho hệ phương trình: \(\left\{ \begin{array}{l}x + ay = 3a\\ - ax + y = 2 - {a^2}\end{array} \right.\;\;\;\left( I \right)\) với \(a\) là tham số.
a) Giải hệ phương trình (I) khi \(a = 1.\)
b) Tìm \(a\) để hệ phương trình (I) có nghiệm duy nhất \(\left( {x;\;y} \right)\) thỏa mãn \(\dfrac{{2y}}{{{x^2} + 3}}\) là số nguyên.
Câu 4 (2 điểm)
Cho phương trình: \({x^2} - 2x + m - 3 = 0\;\;\;\left( 1 \right)\) với \(m\) là tham số,
a) Giải phương trình \(\left( 1 \right)\) khi \(m = 0.\)
b) Tìm tất cả các giá trị của \(m\) để phương trình \(\left( 1 \right)\) có hai nghiệm phân biệt \({x_1},\;\;{x_2}\) thỏa mãn:
\(x_1^2 + 12 = 2{x_2} - {x_1}{x_2}.\)
Câu 5 (3,0 điểm)
Cho đường tròn (O) đường kính AB = 2R, C là trung điểm OA và dây cung MN vuông góc với OA tại C. Gọi K là điểm tùy ý trên cung nhỏ BM (K khác B, M), H là giao điểm của AK và MN.
a) Chứng minh tứ giác BCHK là tứ giác nội tiếp.
b) Chứng minh \(AH.AK = A{M^2}\)
c) Xác định vị trí của điểm K để \(KM + KN + KB\) đạt giá trị lớn nhất và giá trị nhỏ nhất.
Lời giải chi tiết
Câu 1:
\(\begin{array}{l}a)\;A = \;\sqrt {16 + 9} - 2 = \sqrt {25} - 2 \\\;\;\;\;\;\;\;\;= \sqrt {{5^2}} - 2 = 5 - 2 = 3.\\b)\;B = \sqrt {{{\left( {\sqrt 3 - 1} \right)}^2}} + 1 \\\;\;\;\;\;\;\;\;= \left| {\sqrt 3 - 1} \right| + 1 = \sqrt 3 - 1 + 1 \\\;\;\;\;\;\;\;\;= \sqrt 3 \;\;\left( {do\;\;\sqrt 3 - 1 > 0} \right).\end{array}\)
Câu 2:
Cho biểu thức \(P = \left( {\dfrac{{x - 6}}{{x + 3\sqrt x }} - \dfrac{1}{{\sqrt x }} + \dfrac{1}{{\sqrt x + 3}}} \right):\dfrac{{2\sqrt x - 6}}{{x + 1}}\) với \(x > 0,\;\;x \ne 9.\)
a) Rút gọn biểu thức P.
Điều kiện: \(x > 0,\;x \ne 9.\)
\(\begin{array}{l}P = \left( {\dfrac{{x - 6}}{{x + 3\sqrt x }} - \dfrac{1}{{\sqrt x }} + \dfrac{1}{{\sqrt x + 3}}} \right):\dfrac{{2\sqrt x - 6}}{{x + 1}}\\\;\;\; = \left( {\dfrac{{x - 6}}{{\sqrt x \left( {\sqrt x + 3} \right)}} - \dfrac{1}{{\sqrt x }} + \dfrac{1}{{\sqrt x + 3}}} \right):\dfrac{{2\left( {\sqrt x - 3} \right)}}{{x + 1}}\\\;\;\; = \dfrac{{x - 6 - \left( {\sqrt x + 3} \right) + \sqrt x }}{{\sqrt x \left( {\sqrt x + 3} \right)}}.\dfrac{{x + 1}}{{2\left( {\sqrt x - 3} \right)}}\\\;\;\; = \dfrac{{x - 6 - \sqrt x - 3 + \sqrt x }}{{\sqrt x \left( {\sqrt x + 3} \right)}}.\dfrac{{x + 1}}{{2\left( {\sqrt x - 3} \right)}}\\\;\;\; = \dfrac{{\left( {x - 9} \right)\left( {x + 1} \right)}}{{2\sqrt x \left( {x - 9} \right)}} = \dfrac{{x + 1}}{{2\sqrt x }}.\end{array}\)
b) Tìm giá trị của x để \(P = 1.\)
Điều kiện: \(x > 0,\;x \ne 9.\)
\(\begin{array}{l}P = 1 \Leftrightarrow \dfrac{{x + 1}}{{2\sqrt x }} = 1\\ \Leftrightarrow x + 1 = 2\sqrt x \Leftrightarrow x - 2\sqrt x + 1 = 0\\ \Leftrightarrow {\left( {\sqrt x - 1} \right)^2} = 0 \Leftrightarrow \sqrt x - 1 = 0 \\\Leftrightarrow \sqrt x = 1 \Leftrightarrow x = 1\;\;\left( {tm} \right).\end{array}\)
Vậy \(x = 1\) thì \(P = 1.\)
Câu 3:
1) Cho đường thẳng \(\left( d \right):\;\;y = - \dfrac{1}{2}x + 2.\)
a) Tìm \(m\) để đường thẳng \(\left( \Delta \right):\;y = \left( {m - 1} \right)x + 1\) song song với đường thẳng \(\left( d \right).\)
b) Gọi \(A,\;B\) là giao điểm của \(\left( d \right)\) với parabol \(\left( P \right):\;\;y = \dfrac{1}{4}{x^2}.\) Tìm tọa độ điểm \(N\) nằm trên trục hoành sao cho \(NA + NB\) nhỏ nhất.
1) Cho đường thẳng \(\left( d \right):\;\;y = - \dfrac{1}{2}x + 2.\)
a) Tìm \(m\) để đường thẳng \(\left( \Delta \right):\;y = \left( {m - 1} \right)x + 1\) song song với đường thẳng \(\left( d \right).\)
Đường thẳng \(\left( d \right)//\left( \Delta \right) \Leftrightarrow \left\{ \begin{array}{l}m - 1 = - \dfrac{1}{2}\\1 \ne 2\end{array} \right. \Leftrightarrow m = \dfrac{1}{2}.\)
Vậy \(m = \dfrac{1}{2}.\)
b) Gọi \(A,\;B\) là giao điểm của \(\left( d \right)\) với parabol \(\left( P \right):\;\;y = \dfrac{1}{4}{x^2}.\) Tìm tọa độ điểm \(N\) nằm trên trục hoành sao cho \(NA + NB\) nhỏ nhất.
Hoành độ giao điểm của đường thẳng \(\left( d \right)\) và \(\left( P \right)\) là nghiệm của phương trình:
\(\begin{array}{l}\dfrac{1}{4}{x^2} = - \dfrac{1}{2}x + 2 \Leftrightarrow {x^2} + 2x - 8 = 0\;\;\\ \Leftrightarrow \left( {x - 2} \right)\left( {x + 4} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x - 2 = 0\\x + 4 = 0\end{array} \right. \\\Leftrightarrow \left[ \begin{array}{l}x = 2 \Rightarrow y = 1 \Rightarrow A\left( {2;\;1} \right)\\x = - 4 \Rightarrow y = 4 \Rightarrow B\left( { - 4;\;4} \right)\end{array} \right..\end{array}\)
Khi đó \(A\left( {2;\;1} \right),\;\;B\left( { - 4;\;4} \right)\) là hai giao điểm của 2 đồ thị hàm số.
Gọi A’ là điểm đối xứng với A qua Ox thì \(A'\left( {2; - 1} \right)\)
Khi đó ta có: \(NA = NA'\) nên \(NA + NB\,\,\min \Leftrightarrow NA' + NB\,\,\min \)
Mà A’, B nằm khác phía với trục Ox
Nên để NA’ + NB min thì A’, B, N thẳng hàng.
Từ đó suy ra điểm N cần tìm là giao điểm của đường thẳng A’B với trục hoành: \(N\left( {n;0} \right)\)
Gọi phương trình đường thẳng (d’) đi qua hai điểm A’, B là: \(y = ax + b\)
Do A’, B thuộc đường thẳng (d’) nên ta có hệ phương trình:
\(\left\{ \begin{array}{l}2a + b = - 1\\ - 4a + b = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = - \dfrac{5}{6}\\b = \dfrac{2}{3}\end{array} \right.\)
Ta có phương trình đường thẳng (d’) là: \(y = - \dfrac{5}{6}x + \dfrac{2}{3}\)
Khi đó điểm N thuộc đường thẳng d’ và \(N\left( {\dfrac{4}{5};0} \right)\)
Vậy khi \(N\left( {\dfrac{4}{5};0} \right)\) thì \({\left( {NA + NB} \right)_{\min }} = A'B\)\(\, = \sqrt {{{\left( { - 4 - 2} \right)}^2} + {{\left( {4 + 1} \right)}^2}} = \sqrt {61} \).
2) Cho hệ phương trình: \(\left\{ \begin{array}{l}x + ay = 3a\\ - ax + y = 2 - {a^2}\end{array} \right.\;\;\;\left( I \right)\) với \(a\) là tham số.
a) Giải hệ phương trình (I) khi \(a = 1.\)
Thay \(a = 1\) vào hệ phương trình ta được:
\(\left( I \right) \Leftrightarrow \left\{ \begin{array}{l}x + y = 3\\ - x + y = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2y = 4\\x = 3 - y\end{array} \right.\)
\(\Leftrightarrow \left\{ \begin{array}{l}y = 2\\x = 3 - 2 = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y = 2\end{array} \right..\)
Vậy với \(a = 1\) thì hệ phương trình có nghiệm duy nhất \(\left( {x;y} \right) = \left( {1;\;2} \right).\)
b) Tìm \(a\) để hệ phương trình (I) có nghiệm duy nhất \(\left( {x;\;y} \right)\) thỏa mãn \(\dfrac{{2y}}{{{x^2} + 3}}\) là số nguyên.
+) Với \(a = 0\) ta có: \(\left( I \right) \Leftrightarrow \left\{ \begin{array}{l}x = 0\\y = 2\end{array} \right. \Rightarrow \) hệ phương trình có nghiệm duy nhất.
+) Với \(a \ne 0:\) Hệ phương trình có nghiệm duy nhất \( \Leftrightarrow \dfrac{1}{{ - a}} \ne \dfrac{a}{1}\;\;\left( {a \ne 0} \right)\)
\( \Leftrightarrow - {a^2} \ne 1\) (luôn đúng).
Vậy hệ phương trình luôn có nghiệm duy nhất với mọi \(a.\)
Ta có: \(\left( I \right) \Leftrightarrow \left\{ \begin{array}{l}x = 3a - ay\\ - a\left( {3a - ay} \right) + y = 2 - {a^2}\end{array} \right.\)
\(\Leftrightarrow \left\{ \begin{array}{l}x = 3a - ay\\ - 3{a^2} + {a^2}y + y = 2 - {a^2}\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}x = 3a - ay\\y\left( {{a^2} + 1} \right) = 2 + 2{a^2}\end{array} \right. \)
\(\Leftrightarrow \left\{ \begin{array}{l}x = 3a - ay\\y = \dfrac{{2{a^2} + 2}}{{{a^2} + 1}} = 2\end{array} \right. \)
\(\Leftrightarrow \left\{ \begin{array}{l}x = 3a - 2a = a\\y = 2\end{array} \right..\)
\( \Rightarrow \) Hệ phương trình có nghiệm duy nhất \(\left( {x;\;y} \right) = \left( {a;\;2} \right).\)
Ta có: \(\dfrac{{2y}}{{{x^2} + 3}} = \dfrac{{2.2}}{{{a^2} + 3}} = \dfrac{4}{{{a^2} + 3}}.\)
\(\dfrac{{2y}}{{{x^2} + 3}} \in Z \Leftrightarrow \dfrac{4}{{{a^2} + 3}} \in Z\)
\(\Leftrightarrow \left( {{a^2} + 3} \right) \in U\left( 4 \right)\)
Mà \(U\left( 4 \right) = \left\{ { \pm 1;\; \pm 2;\; \pm 4} \right\}.\)
Lại có: \({a^2} + 3 \ge 3\;\;\forall \;a\)
\(\Rightarrow {a^2} + 3 = 4 \Leftrightarrow {a^2} = 1 \)
\(\Leftrightarrow \left[ \begin{array}{l}a = 1\\a = - 1\end{array} \right..\)
Vậy \(a = \pm 1\) thỏa mãn điều kiện bài toán.
Câu 4:
Cho phương trình: \({x^2} - 2x + m - 3 = 0\;\;\;\left( 1 \right)\) với \(m\) là tham số,
a) Giải phương trình \(\left( 1 \right)\) khi \(m = 0.\)
Thay \(m = 0\) vào phương trình \(\left( 1 \right)\) ta có:
\(\left( 1 \right) \Leftrightarrow {x^2} - 2x - 3 = 0\)
\(\Leftrightarrow \left( {x - 3} \right)\left( {x + 1} \right) = 0\)
\(\Leftrightarrow \left[ \begin{array}{l}x - 3 = 0\\x + 1 = 0\end{array} \right. \)
\(\Leftrightarrow \left[ \begin{array}{l}x = 3\\x = - 1\end{array} \right..\)
Vậy với \(m = 0\) thì phương trình \(\left( 1 \right)\) có hai nghiệm phân biệt \(x = - 1\) và \(x = 3.\)
b) Tìm tất cả các giá trị của \(m\) để phương trình \(\left( 1 \right)\) có hai nghiệm phân biệt \({x_1},\;\;{x_2}\) thỏa mãn:
\(x_1^2 + 12 = 2{x_2} - {x_1}{x_2}.\)
Phương trình \(\left( 1 \right)\) có hai nghiệm phân biệt \( \Leftrightarrow \Delta ' > 0 \Leftrightarrow 1 - m + 3 > 0 \Leftrightarrow m < 4.\)
Áp dụng hệ thức Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2\\{x_1}{x_2} = m - 3\end{array} \right. \)
\(\Leftrightarrow \left\{ \begin{array}{l}{x_2} = 2 - {x_1}\;\;\;\;\;\;\left( 1 \right)\\{x_1}{x_2} = m - 3\;\;\;\;\;\left( 2 \right)\end{array} \right.\)
Theo đề bài ta có: \(x_1^2 + 12 = 2{x_2} - {x_1}{x_2}\;\;\;\left( 3 \right)\)
Thế \(\left( 1 \right)\) vào \(\left( 2 \right)\) ta có:
\(\begin{array}{l}\;\;\;\;\;x_1^2 + 12 = 2\left( {2 - {x_1}} \right) - {x_1}\left( {2 - {x_1}} \right)\\ \Leftrightarrow x_1^2 + 12 = 4 - 2{x_1} - 2{x_1} + x_1^2\\ \Leftrightarrow - 4{x_1} = 8 \Leftrightarrow {x_1} = - 2\\ \Rightarrow {x_2} = 2 - {x_1} = 4.\\ \Rightarrow {x_1}{x_2} = m - 3\\ \Leftrightarrow m - 3 = - 8 \Leftrightarrow m = - 5\;\;\left( {tm} \right).\end{array}\)
Vậy \(m = - 5.\)
Câu 5.
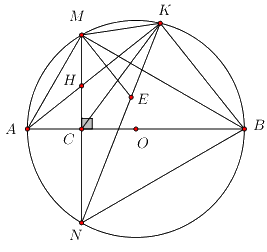
a) Ta có \(\widehat {AKB} = {90^0}\) (góc nội tiếp chắn nửa đường tròn).
Xét tứ giác BCHK có \(\widehat {BCH} + \widehat {BKH} = {90^0} + {90^0} \Rightarrow \) Tứ giác BCHK là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng 1800)
b) Ta có \(OA \bot MN\) tại C \( \Rightarrow C\) là trung điểm của MN (quan hệ vuông góc giữa đường kính và dây cung).
\( \Rightarrow \Delta AMN\) có AC là đường cao đồng thời là trung tuyến
\( \Rightarrow \Delta AMN\) cân tại \(A \Rightarrow AM = AN \Rightarrow \) sđ cung AM = sđ cung AN.
\( \Rightarrow \widehat {AMN} = \widehat {AKM}\) (hai góc nội tiếp chắn hai cung bằng nhau)
Xét tam giác AMN và AKM có:
\(\widehat {MAK}\) chung;
\(\widehat {AMN} = \widehat {AKM}\,\,\left( {cmt} \right)\);
\( \Rightarrow \Delta AMH \sim \Delta AKM\,\,\,\left( {g.g} \right)\)
\(\Rightarrow \dfrac{{AM}}{{AK}} = \dfrac{{AH}}{{AM}} \Rightarrow A{M^2} = AH.AK\)
c) Lấy điểm E thuộc KN sao cho \(KM = KE\).
Xét tam giác vuông AMB có: \(A{M^2} = AC.AB = \dfrac{R}{2}.2R = {R^2} \)
\(\Rightarrow AM = R\) (hệ thức lượng trong tam giác vuông)
\( \Rightarrow \sin \widehat {ABM} = \dfrac{{AM}}{{AB}} = \dfrac{R}{{2R}} = \dfrac{1}{2} \)\(\,\Rightarrow \widehat {ABM} = {30^0}\)\( \Rightarrow \widehat {MBN} = {60^0}\) (tính đối xứng).
\( \Rightarrow \widehat {MKE} = \widehat {MKN} = \widehat {MBN} = {60^0}\) (hai góc nội tiếp cùng chắn cung MN).
\( \Rightarrow \Delta AKE\) đều \( \Rightarrow KM = KE = ME\).
Ta có AB là trung trực của MN \( \Rightarrow BM = BN\)
Lại có \(\widehat {MBN} = {60^0}\,\,\left( {cmt} \right) \Rightarrow \Delta BMN\) đều \( \Rightarrow MB = MN = BN\) và \(\widehat {BMN} = {60^0}\)
\(\begin{array}{l} \Rightarrow \widehat {BMN} = \widehat {KME} = {60^0}\\ \Rightarrow \widehat {BMN} - \widehat {BME} = \widehat {KME} - \widehat {BME}\\ \Leftrightarrow \widehat {EMN} = \widehat {KMB}\end{array}\)
Xét tam giác KMB và tam giác EMN có:
KM = EM;
MB = MN;
\(\widehat {EMN} = \widehat {KMB}\,\,\left( {cmt} \right);\)
\( \Rightarrow \Delta KMB = \Delta EMN\,\,\left( {c.g.c} \right)\)
\( \Rightarrow KB = EN\) (hai cạnh tương ứng)
\( \Rightarrow S = KM + KN + KB\)
\(= KE + \left( {KE + EN} \right) + EN \)
\(= 2\left( {KE + EN} \right) = 2KN\)
KN lớn nhất khi và chỉ khi KN là đường kính của đường tròn O, khi đó KN = 2R và \({S_{\max }} = 4R\)
KN nhỏ nhất khi và chỉ khi \(K \equiv M \Rightarrow KN = MN \Rightarrow {S_{\min }} = 2MN\)
Xét tam giác vuông AMB cos \(M{C^2} = AC.BC = \dfrac{R}{2}.\dfrac{{3R}}{2} = \dfrac{{3{R^2}}}{4} \)
\(\Rightarrow MC = \dfrac{{R\sqrt 3 }}{2} \Rightarrow MN = R\sqrt 3 \)
\(\Rightarrow {S_{\min }} = 2R\sqrt 3 \)
Vậy \({\left( {KM + KN + KB} \right)_{\max }} = 4R\) và \({\left( {KM + KN + KB} \right)_{\min }} = 2R\sqrt 3 \).
Đề thi vào lớp 10 môn Toán là một bước ngoặt quan trọng trong quá trình học tập của học sinh. Để đạt kết quả tốt, việc luyện tập thường xuyên với các đề thi thử là vô cùng cần thiết. Đề số 10 mà giaitoan.edu.vn cung cấp là một công cụ hữu ích giúp học sinh làm quen với cấu trúc đề thi, rèn luyện kỹ năng giải toán và tự đánh giá năng lực của bản thân.
Đề thi vào lớp 10 môn Toán thường bao gồm các phần sau:
Các dạng bài tập thường gặp trong đề thi bao gồm:
Đề số 10 bao gồm các câu hỏi trắc nghiệm và tự luận, tập trung vào các kiến thức trọng tâm của chương trình Toán lớp 9. Các câu hỏi trắc nghiệm kiểm tra khả năng nắm vững lý thuyết và vận dụng nhanh các công thức. Các câu hỏi tự luận yêu cầu học sinh trình bày lời giải chi tiết, thể hiện khả năng tư duy và giải quyết vấn đề.
Ví dụ, một câu hỏi tự luận trong đề thi có thể là:
“Cho tam giác ABC vuông tại A, đường cao AH. Gọi D và E lần lượt là hình chiếu vuông góc của H lên AB và AC. Chứng minh rằng ADHE là hình chữ nhật.”
Để giải bài toán này, học sinh cần nắm vững các kiến thức về tam giác vuông, đường cao trong tam giác vuông, và các tính chất của hình chữ nhật.
Giaitoan.edu.vn cung cấp hướng dẫn giải và đáp án chi tiết cho từng câu hỏi trong Đề số 10. Các lời giải được trình bày rõ ràng, dễ hiểu, giúp học sinh nắm vững phương pháp giải và tự tin hơn khi làm bài.
Ngoài ra, chúng tôi còn cung cấp các bài giảng video, bài tập luyện tập và các tài liệu tham khảo khác để giúp học sinh ôn tập kiến thức và nâng cao kỹ năng giải toán.
Để đạt kết quả tốt trong kỳ thi tuyển sinh vào lớp 10 môn Toán, học sinh cần:
Giaitoan.edu.vn là một nền tảng học toán online uy tín, cung cấp các khóa học chất lượng, đề thi thử đa dạng và đội ngũ giáo viên giàu kinh nghiệm. Chúng tôi cam kết đồng hành cùng bạn trên con đường chinh phục kiến thức và đạt được thành công trong kỳ thi tuyển sinh vào lớp 10.
Hãy truy cập giaitoan.edu.vn ngay hôm nay để khám phá thêm nhiều tài liệu học tập hữu ích và bắt đầu hành trình luyện thi vào lớp 10 môn Toán của bạn!
| Dạng bài tập | Mức độ khó | Lời khuyên |
|---|---|---|
| Giải phương trình | Trung bình | Nắm vững các phương pháp giải phương trình cơ bản. |
| Chứng minh hình học | Khó | Vẽ hình chính xác và sử dụng các định lý, tính chất hình học phù hợp. |
| Bài toán về số học | Trung bình | Sử dụng các tính chất chia hết, ước số và số nguyên tố. |