Chào mừng bạn đến với bài viết phân tích và giải chi tiết Đề số 27 - Đề thi vào lớp 10 môn Toán tại giaitoan.edu.vn. Đây là một trong những đề thi thử quan trọng giúp học sinh làm quen với cấu trúc đề thi và rèn luyện kỹ năng giải toán.
Chúng tôi cung cấp lời giải chi tiết, dễ hiểu, cùng với các phương pháp giải nhanh và hiệu quả, giúp bạn tự tin đối mặt với kỳ thi sắp tới.
Đề thi vào lớp 10 môn Toán - Đề số 27 có đáp án và lời giải chi tiết
Đề bài
Câu 1 (1 điểm):
a) Tính \(H = \sqrt {81} - \sqrt {16} .\)
b) Tìm điều kiện của \(x\) để \(\sqrt {x + 2} \) có nghĩa.
Câu 2 (1,0 điểm):
Giải hệ phương trình: \(\left\{ \begin{array}{l}x - 2y = 3\\3x + 2y = 1\end{array} \right..\)
Câu 3 (1,0 điểm):
Rút gọn biểu thức \(M = \left( {\dfrac{{x + \sqrt y + \sqrt {xy} - 1}}{{\sqrt x + 1}} + 1} \right).\left( {\sqrt x - \sqrt y } \right)\) (với \(x \ge 0,\;y \ge 0\)).
Câu 4 (1,0 điểm):
a) Giải phương trình \({x^2} - 2x - 8 = 0.\)
b) Cho phương trình \({x^2} + 6x + m = 0\) (với m là tham số). Tìm tất cả các giá trị của m để phương trình đã cho có hai nghiệm phân biệt.
Câu 5 (1,0 điểm):
Trong mặt phẳng tọa độ \(Oxy,\) cho đường thẳng \(\left( d \right):\;y = - 3x + b\) và parabol \(\left( P \right):\;\;y = 2{x^2}.\)
a) Xác định hệ số b để (d) đi qua điểm \(A\left( {0;\;1} \right).\)
b) Với \(b = - 1,\) tìm tọa độ giao điểm của (d) và (P) bằng phương pháp đại số.
Câu 6 (1,0 điểm):
Để chuẩn bị cho mùa giải sắp tới, một vận động viên đua xe ở Đồng Tháp đã luyện tập leo dốc và đổ dốc trên cầu Cao Lãnh. Biết rằng đoạn leo dốc và đổ dốc ở hai bên đầu cầu có độ dài cùng bằng \(1km.\) Trong một lần luyện tập, vận động viên khi đổ dốc nhanh hơn vận tốc khi leo dốc là \(9km/h\) và tổng thời gian hoàn thành là \(3\) phút. Tính vận tốc leo dốc của vận động viên trong lần luyện tập đó.
Câu 7. Nhằm tiếp tục đẩy mạnh phong trào xây dựng trường học Xanh – Sạch – Đẹp, trường THCS A đã thiết kế một khuôn viên để trồng hoa có dạng hình tam giác vuông (như hình bên, biết rằng \(\Delta MNK\) vuông tại M, \(MN = 6m,\,\,MK = 8m,\,\,MH \bot NK\)). Nhà trường trồng hoa mười giờ dọc các đoạn NK, MH.
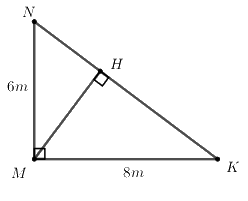
a) Tính độ dài các đoạn NK, MH.
b) Biết rằng chi phí trồng hoa mười giờ là 20000 đồng trên mỗi mét chiều dài. Tính tổng chi phí để trồng các luống hoa mười giờ đó.
Câu 8. Cho tam giác ABC vuông tại A \(\left( {AB < AC} \right)\), đường cao \(AH\,\,\left( {H \in BC} \right)\), trên cạnh BC lấy điểm D sao cho \(BD = BA\), vẽ CE vuông góc AD \(\left( {E \in AD} \right)\).
a) Chứng minh tứ giác AHEC là tứ giác nội tiếp.
b) Chứng minh \(DA.HE = DH.AC\)
c) Chứng minh tam giác \(EHC\) là tam giác cân.
Lời giải chi tiết
Câu 1:
a) Tính \(H = \sqrt {81} - \sqrt {16} .\)
\(H = \sqrt {81} - \sqrt {16} = \sqrt {{9^2}} - \sqrt {{4^2}} = 9 - 4 = 5.\)
b) Tìm điều kiện của \(x\) để \(\sqrt {x + 2} \) có nghĩa.
Biểu thức \(\sqrt {x + 2} \) có nghĩa \( \Leftrightarrow x + 2 \ge 0 \Leftrightarrow x \ge - 2.\)
Câu 2:
Giải hệ phương trình: \(\left\{ \begin{array}{l}x - 2y = 3\\3x + 2y = 1\end{array} \right..\)
\(\left\{ \begin{array}{l}x - 2y = 3\\3x + 2y = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}4x = 4\\2y = x - 3\end{array} \right. \)
\(\Leftrightarrow \left\{ \begin{array}{l}x = 1\\2y = - 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y = - 1\end{array} \right..\)
Vậy hệ phương trình có nghiệm duy nhất \(\left( {x;\;y} \right) = \left( {1; - 1} \right).\)
Câu 3:
Rút gọn biểu thức \(M = \left( {\dfrac{{x + \sqrt y + \sqrt {xy} - 1}}{{\sqrt x + 1}} + 1} \right).\left( {\sqrt x - \sqrt y } \right)\) (với \(x \ge 0,\;y \ge 0\)).
\(\begin{array}{l}M = \left( {\dfrac{{x + \sqrt y + \sqrt {xy} - 1}}{{\sqrt x + 1}} + 1} \right).\left( {\sqrt x - \sqrt y } \right)\\\;\;\;\; = \dfrac{{x + \sqrt y + \sqrt {xy} - 1 + \sqrt x + 1}}{{\sqrt x + 1}}.\left( {\sqrt x - \sqrt y } \right)\\\;\;\;\; = \dfrac{{x + \sqrt y + \sqrt {xy} + \sqrt x }}{{\sqrt x + 1}}.\left( {\sqrt x - \sqrt y } \right)\\\;\;\;\; = \dfrac{{\sqrt x \left( {\sqrt x + 1} \right) + \sqrt y \left( {\sqrt x + 1} \right)}}{{\sqrt x + 1}}.\left( {\sqrt x - \sqrt y } \right)\\\;\;\;\; = \dfrac{{\left( {\sqrt x + 1} \right)\left( {\sqrt x + \sqrt y } \right)}}{{\sqrt x + 1}}.\left( {\sqrt x - \sqrt y } \right)\\\;\;\;\; = \left( {\sqrt x + \sqrt y } \right).\left( {\sqrt x - \sqrt y } \right)\\\;\;\;\; = x - y.\end{array}\)
Câu 4:
a) Giải phương trình \({x^2} - 2x - 8 = 0.\)
Ta có: \(\Delta ' = 1 + 8 = 9 > 0 \Rightarrow \) phương trình có hai nghiệm phân biệt: \(\left[ \begin{array}{l}{x_1} = 1 + \sqrt 9 = 4\\{x_2} = 1 - \sqrt 9 = - 2\end{array} \right..\)
Vậy phương trình đã cho có tập nghiệm \(S = \left\{ { - 2;\;4} \right\}.\)
b) Cho phương trình \({x^2} + 6x + m = 0\) (với m là tham số). Tìm tất cả các giá trị của m để phương trình đã cho có hai nghiệm phân biệt.
Phương trình đã cho có hai nghiệm phân biệt \( \Leftrightarrow \Delta ' > 0\)
\( \Leftrightarrow 9 - m > 0 \Leftrightarrow m < 9.\)
Vậy phương trình đã cho có hai nghiệm phân biệt khi \(m < 9.\)
Câu 5:
Trong mặt phẳng tọa độ \(Oxy,\) cho đường thẳng \(\left( d \right):\;y = - 3x + b\) và parabol \(\left( P \right):\;\;y = 2{x^2}.\)
a) Xác định hệ số b để (d) đi qua điểm \(A\left( {0;\;1} \right).\)
Ta có: (d) đi qua điểm \(A\left( {0;\;1} \right) \Rightarrow 1 = - 3.0 + b \Leftrightarrow b = 1.\)
Vậy \(b = 1\) là giá trị cần tìm.
b) Với \(b = - 1,\) tìm tọa độ giao điểm của (d) và (P) bằng phương pháp đại số.
Với \(b = - 1\) ta có: \(\left( d \right):\;y = - 3x - 1.\)
Phương trình hoành độ của \(\left( d \right)\) và \(\left( P \right)\) là: \( - 3x - 1 = 2{x^2} \Leftrightarrow 2{x^2} + 3x + 1 = 0\)
\( \Leftrightarrow \left( {x + 1} \right)\left( {2x + 1} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = - \dfrac{1}{2}\end{array} \right..\)
+) Với \(x = - 1 \Rightarrow y = 2.{\left( { - 1} \right)^2} = 2\) \( \Rightarrow A\left( { - 1;\;2} \right).\)
+) Với \(x = - \dfrac{1}{2} \Rightarrow y = 2.{\left( { - \dfrac{1}{2}} \right)^2} = \dfrac{1}{2}\) \( \Rightarrow B\left( { - \dfrac{1}{2};\;\dfrac{1}{2}} \right).\)
Vậy với \(b = - 1\) thì \(\left( d \right)\) cắt \(\left( P \right)\) tại hai điểm phân biệt \(A\left( { - 1;\;2} \right),\;\;B\left( { - \dfrac{1}{2};\;\dfrac{1}{2}} \right).\)
Câu 6:
Để chuẩn bị cho mùa giải sắp tới, một vận động viên đua xe ở Đồng Tháp đã luyện tập leo dốc và đổ dốc trên cầu Cao Lãnh. Biết rằng đoạn leo dốc và đổ dốc ở hai bên đầu cầu có độ dài cùng bằng \(1km.\) Trong một lần luyện tập, vận động viên khi đổ dốc nhanh hơn vận tốc khi leo dốc là \(9km/h\) và tổng thời gian hoàn thành là \(3\) phút. Tính vận tốc leo dốc của vận động viên trong lần luyện tập đó.
Gọi vận tốc khi leo dốc của vận động viên trong lần luyện tập đó là \(x\;\left( {km/h} \right),\;\;\left( {x > 0} \right).\)
Khi đó vận tốc của vận động viên khi đổ dốc trong lần luyện tập đó là: \(x + 9\;\;\left( {km/h} \right).\)
Thời gian vận động viên leo dốc và đổ dốc trong lần luyện tập đó lần lượt là: \(\dfrac{1}{x}\;\;\left( h \right),\;\;\dfrac{1}{{x + 9}}\;\;\left( h \right).\)
Theo đề bài ta có phương trình: \(\dfrac{1}{x} + \dfrac{1}{{x + 9}} = \dfrac{3}{{60}} = \dfrac{1}{{20}}\)
\(\begin{array}{l} \Leftrightarrow 20\left( {x + 9} \right) + 20x = x\left( {x + 9} \right)\\ \Leftrightarrow 20x + 180 + 20x = {x^2} + 9x\\ \Leftrightarrow {x^2} - 31x - 180 = 0\\ \Leftrightarrow \left( {x - 36} \right)\left( {x + 5} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 36 = 0\\x + 5 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 36\;\;\;\left( {tm} \right)\\x = - 5\;\;\left( {ktm} \right)\end{array} \right..\end{array}\)
Vậy vận tốc khi leo dốc của vận động viên trong lần luyện tập đó là \(36\;km/h.\)
Câu 7.
Nhằm tiếp tục đẩy mạnh phong trào xây dựng trường học Xanh – Sạch – Đẹp, trường THCS A đã thiết kế một khuôn viên để trồng hoa có dạng hình tam giác vuông (như hình bên, biết rằng \(\Delta MNK\) vuông tại M, \(MN = 6m,\,\,MK = 8m,\,\,MH \bot NK\)). Nhà trường trồng hoa mười giờ dọc các đoạn NK, MH.
a)
Áp dụng định lí Pi-ta-go trong tam giác vuông MNK có:Tính độ dài các đoạn NK, MH.
\(N{K^2} = M{N^2} + M{K^2} = {6^2} + {8^2} = 100\)
\(\Rightarrow NK = 10\,\,\left( m \right)\)
Áp dụng hệ thức lượng trong tam giác vuông MNK có:
\(MN.MK = MH.NK\)
\(\Rightarrow NH = \dfrac{{MN.MK}}{{NK}} = \dfrac{{6.8}}{{10}} = 4,8\,\,\left( m \right)\)
b) Biết rằng chi phí trồng hoa mười giờ là 20000 đồng trên mỗi mét chiều dài. Tính tổng chi phí để trồng các luống hoa mười giờ đó.
Tổng độ dài hai đoạn NK và MH là \(10 + 4,8 = 14,8\,\,\left( m \right)\)
Do đó chi phí trồng hoa mười giờ là: \(14,8.20000 = 296000\) (đồng)
Câu 8.
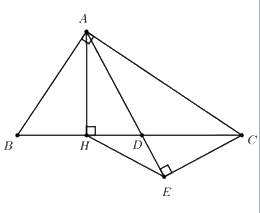
Cho tam giác ABC vuông tại A \(\left( {AB < AC} \right)\), đường cao \(AH\,\,\left( {H \in BC} \right)\), trên cạnh BC lấy điểm D sao cho \(BD = BA\), vẽ CE vuông góc AD \(\left( {E \in AD} \right)\).
a) Chứng minh tứ giác AHEC là tứ giác nội tiếp.
Ta có \(\angle AHC = \angle AEC = {90^0}\,\,\left( {gt} \right) \Rightarrow \) Tứ giác AHEC là tứ giác nội tiếp (Hai đỉnh H và E kề cạnh HE cùng nhìn cạnh AC dưới góc \({90^0}\))
b) Chứng minh \(DA.HE = DH.AC\)
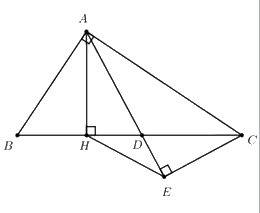
\( \Rightarrow \angle ACH = \angle AEH\) (hai góc nội tiếp cùng chắn cung AH)
Xét \(\Delta ADC\) và \(\Delta HDE\) có:
\(\angle ADC = \angle HDE\) (đối đỉnh);
\(\begin{array}{l}\angle ACH = \angle AEH\,\,\left( {cmt} \right)\\ \Rightarrow \Delta ADC \sim \Delta HDE\,\,\left( {g.g} \right) \\ \Rightarrow \dfrac{{DA}}{{DH}} = \dfrac{{AC}}{{HE}}\\ \Rightarrow DA.HE = DH.AC\;\;\left( {dpcm} \right)\end{array}\)
c) Chứng minh tam giác \(EHC\) là tam giác cân.
Cách 1:
Ta có: \(AB = BD\;\;\left( {gt} \right) \Rightarrow \Delta ABD\) cân tại \(B \Rightarrow \angle BAD = \angle ADB\) (hai góc kề đáy).
Mà \(\angle BAC = {90^0}\) \( \Rightarrow \angle BAD + \angle DAC = {90^0}\) \( \Leftrightarrow \angle ADB + \angle DAC = {90^0}\;\;\left( 1 \right)\)
Xét \(\Delta AHD\) vuông tại \(H\) ta có:
\(\angle HDA + \angle HAD = {90^0}\) \( \Leftrightarrow \angle BDA + \angle HAD = {90^0}\;\;\;\left( 2 \right)\)
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) \( \Rightarrow \angle HAD = \angle DAC\;\;hay\;\;\angle HAE = \angle EAC\;\;\;\left( 3 \right)\)
Xét tứ giác \(AHEC\) nội tiếp ta có:
\(\angle EAC = \angle EHC\) (hai góc nội tiếp cùng chắn cung EC) (4)
\(\angle HAE = \angle HCE\) (hai góc nội tiếp cùng chắn cung HE) (5)
Từ \(\left( 4 \right)\) và \(\left( 5 \right) \Rightarrow \angle CHE = \angle HCE\;\;\left( { = \angle HAE = \angle EAC} \right).\)
\( \Rightarrow \Delta HEC\) cân tại \(E\;\;\left( {dpcm} \right).\)
Cách 2:
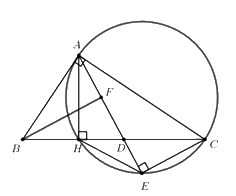
Do \(AB \bot AC \Rightarrow AB\) là tiếp tuyến của đường tròn đường kính AC
\( \Rightarrow \angle BAE = \angle ACE\) (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung AE)
Gọi F là trung điểm của AD, do tam giác ABD cân tại B \(\left( {BA = BD} \right)\)
\( \Rightarrow BF \bot AD\) (trung tuyến đồng thời là đường cao)
Và \(\angle ABF = \angle DBF\,\,\left( 1 \right)\) (trung tuyến đồng thời là đường phân giác).
Xét tam giác ABF và tam giác CAE có:
\(\begin{array}{l}\angle AFB = \angle CEA = {90^0};\\\angle BAF = \angle ACE\,\,\left( {cmt} \right)\\ \Rightarrow \Delta ABF \sim \Delta CAE\,\,\left( {g.g} \right) \\\Rightarrow \angle ABF = \angle CAE\end{array}\)
Lại có: \(\angle CAE = \angle CHE\) (hai góc nội tiếp cùng chắn cung EC) \( \Rightarrow \angle ABF = \angle CHE\,\,\left( 2 \right)\)
Ta có: \(\left\{ \begin{array}{l}BF \bot AE\,\,\left( {cmt} \right)\\CE \bot AE\,\,\left( {gt} \right)\end{array} \right.\\ \Rightarrow BF//CE \Rightarrow \angle DBF = \angle HCE\,\,\,\left( 3 \right)\) (so le trong)
Từ (1), (2) và (3) \( \Rightarrow \angle CHE = \angle HCE \Rightarrow \Delta EHC\) cân tại E (đpcm).
Đề thi vào lớp 10 môn Toán là một kỳ thi quan trọng đánh giá năng lực học tập của học sinh sau nhiều năm học tập ở bậc THCS. Việc làm quen với các dạng đề thi khác nhau, đặc biệt là các đề thi thử, là một bước chuẩn bị không thể thiếu để đạt kết quả tốt nhất.
Đề thi vào lớp 10 môn Toán thường bao gồm các dạng bài tập sau:
Đề số 27 bao gồm các câu hỏi thuộc nhiều lĩnh vực khác nhau của chương trình Toán lớp 9. Đề thi có độ khó vừa phải, tập trung vào các kiến thức cơ bản và nâng cao. Việc giải đề thi này đòi hỏi học sinh phải nắm vững kiến thức, kỹ năng giải toán và khả năng vận dụng linh hoạt các công thức, định lý.
Dưới đây là lời giải chi tiết cho từng câu hỏi trong Đề số 27:
Lời giải:...
Lời giải:...
Lời giải:...
Để giải quyết các bài toán trong đề thi vào lớp 10 môn Toán một cách hiệu quả, bạn có thể áp dụng các phương pháp sau:
Việc luyện tập thường xuyên với các đề thi thử khác nhau là một cách hiệu quả để nâng cao kỹ năng giải toán và làm quen với cấu trúc đề thi. Ngoài ra, bạn cũng nên dành thời gian ôn tập lại các kiến thức cơ bản và nâng cao trong chương trình Toán lớp 9.
Để hỗ trợ quá trình ôn tập và luyện thi, bạn có thể tham khảo các tài liệu sau:
Trước khi bước vào kỳ thi, hãy giữ tâm lý thoải mái, tự tin và có chế độ ăn uống, nghỉ ngơi hợp lý. Trong quá trình làm bài, hãy đọc kỹ đề bài, phân bổ thời gian hợp lý và kiểm tra lại kết quả trước khi nộp bài.
Chúc các bạn thành công!
| Dạng bài tập | Mức độ khó | Lời khuyên |
|---|---|---|
| Đại số | Trung bình | Nắm vững các công thức và phương pháp giải. |
| Hình học | Khó | Vẽ hình chính xác và áp dụng các định lý. |
| Số học | Dễ | Hiểu rõ các khái niệm và tính chất. |