Giaitoan.edu.vn xin giới thiệu bộ đề thi tuyển sinh vào lớp 10 môn Toán tỉnh Vĩnh Phúc năm 2023. Đây là tài liệu ôn tập vô cùng quan trọng dành cho các em học sinh đang chuẩn bị cho kỳ thi sắp tới.
Chúng tôi cung cấp đầy đủ các đề thi chính thức, đáp án chi tiết và phương pháp giải bài tập hiệu quả.
Phần I: Trắc nghiệm Câu 1: Biểu thức \(\sqrt {120 - 6x} \) có nghĩa khi A. \(x \ge 20\) B. \(x \le 20\) C. \(x < 20\) D. \(x > 20\)
Phần I: Trắc nghiệm
Câu 1: Biểu thức \(\sqrt {120 - 6x} \) có nghĩa khi
A. \(x \ge 20\)
B. \(x \le 20\)
C. \(x < 20\)
D. \(x > 20\)
Câu 2: Hàm số \(y = \left( {m - 2023} \right)x + 2024\) (với \(m\) là tham số) đồng biến trên \(\mathbb{R}\) khi
A. \(m > 2023\)
B. \(m \ge 2024\)
C. \(m \le 2023\)
D. \(m < 2024\)
Câu 3: Phương trình \(3{x^2} - 7x + 4 = 0\) có hai nghiệm \({x_1},{x_2}\). Khi đó \(\left| {{x_1} - {x_2}} \right|\) bằng
A. \(\frac{7}{3}\)
B. \( - \frac{1}{3}\)
C. \(\frac{4}{3}\)
D. \(\frac{1}{3}\)
Câu 4: Cho tam giác ABC vuông tại \(A\), biết độ dài các cạnh \(AB = 6\;{\rm{cm}},AC = 8\;{\rm{cm}}\). Bán kính đường tròn ngoại tiếp tam giác ABC bằng
A. \(10\;{\rm{cm}}\)
B. \(5\sqrt 2 \;{\rm{cm}}\)
C. \(5\;{\rm{cm}}\)
D. \(\sqrt {10} \;{\rm{cm}}\)
Phần II: Tự luận
Câu 5: Giải hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{3x + 2y = 5}\\{x - 3y = 9}\end{array}} \right.\)
Câu 6: Cho biểu thức \(A = \frac{{x\sqrt x {\rm{ \;}} + 1}}{{x - 1}} - \frac{{x - 1}}{{\sqrt x {\rm{ \;}} + 1}}\) (với \(\left. {x \ge 0;x \ne 1} \right)\).
a) Rút gọn biểu thức \(A\).
b) Tìm tất cả các số nguyên \(x\) để \(A\) nhận giá trị nguyên.
Câu 7: Cho phương trình \({x^2} - \left( {2m + 1} \right)x + {m^2} - 1 = 0\) (1) với \(m\) là tham số.
a) Giải phương trình (1) khi \(m = 5\).
b) Tìm tất cả các giá trị của tham số \(m\) để phương trình (1) có 2 nghiệm \({x_1},{x_2}\) thỏa mãn điều kiện \(\left( {x_1^2 - 2m{x_1} + {m^2}} \right)\left( {{x_2} + 1} \right) = 4.\;\)
Câu 8: Một hãng taxi công nghệ cao có giá cước (giá tiền khách hàng phải trả cho mỗi km) được tính theo các mức như sau:
Mức 1: Giá mở cửa cho \(1\;{\rm{km}}\) đầu tiên là 20000 đồng;
Mức 2: Từ trên \(1\;{\rm{km}}\) đến \(25\;{\rm{km}}\);
Mức 3: Từ trên \(25\;{\rm{km}}\).
Biết rằng anh \({\rm{A}}\) đi \(32\;{\rm{km}}\) phải trả tiền taxi là 479500 đồng còn chị \({\rm{B}}\) đi \(41\;{\rm{km}}\) phải trả 592000 đồng. Hỏi giá cước của hãng taxi trên ở mức 2 và mức 3 là bao nhiêu? Nếu khách hàng đi \(24\;{\rm{km}}\) thì phải trả taxi bao nhiêu tiền?
Câu 9: Cho đường tròn \(\left( O \right)\) và \(BC\) là một dây cung khác đường kính của \(\left( O \right),A\) là điểm di động trên cung lớn \(BC\) sao cho \(AC > AB\left( {A \ne B} \right)\). Gọi \(D\) là chân đường phân giác trong góc \(\widehat {BAC}\) \(\left( {D \in BC} \right)\). Đường thẳng đi qua \(O\) và vuông góc với \(BC\) cắt đường thẳng \(AD\) tại \(E\). Kẻ \(EH,EK\) lần lượt vuông góc với \(AB\) và \(AC\left( {H \in AB,K \in AC} \right)\).
a) Chứng minh \(EHAK\) là tứ giác nội tiếp.
b) Gọi \(F\) là tâm đường tròn nội tiếp tam giác \(ABC\). Chứng minh điểm \(E\) thuộc đường tròn \(\left( O \right)\) và \(E\) là tâm đường tròn ngoại tiếp tam giác \(BCF\).
c) Gọi \(M,N,I\) lần lượt là trung điểm của các đoạn thẳng \(AE,BE\) và \(BC\). Chứng minh \(BMDN\) là tứ giác nội tiếp. Xác định vị trí điểm \(A\) để bốn điểm \(H,N,I,K\) thẳng hàng.
Câu 10: Cho các số thực a, b, c sao cho phương trình \(a{x^2} + bx + c + 2023 = 0\) nhận \(x = 1\)là nghiệm. Tìm giá trị nhỏ nhất của biểu thức:
\(P = \sqrt {3{a^2} - 2ab + 3{b^2}} + \sqrt {5{b^2} - 6bc + 5{c^2}} + \sqrt {6{c^2} - 8ca + 6{a^2}} \)
----- HẾT -----
Phần I: Trắc nghiệm
Câu 1: Biểu thức \(\sqrt {120 - 6x} \) có nghĩa khi
A. \(x \ge 20\)
B. \(x \le 20\)
C. \(x < 20\)
D. \(x > 20\)
Câu 2: Hàm số \(y = \left( {m - 2023} \right)x + 2024\) (với \(m\) là tham số) đồng biến trên \(\mathbb{R}\) khi
A. \(m > 2023\)
B. \(m \ge 2024\)
C. \(m \le 2023\)
D. \(m < 2024\)
Câu 3: Phương trình \(3{x^2} - 7x + 4 = 0\) có hai nghiệm \({x_1},{x_2}\). Khi đó \(\left| {{x_1} - {x_2}} \right|\) bằng
A. \(\frac{7}{3}\)
B. \( - \frac{1}{3}\)
C. \(\frac{4}{3}\)
D. \(\frac{1}{3}\)
Câu 4: Cho tam giác ABC vuông tại \(A\), biết độ dài các cạnh \(AB = 6\;{\rm{cm}},AC = 8\;{\rm{cm}}\). Bán kính đường tròn ngoại tiếp tam giác ABC bằng
A. \(10\;{\rm{cm}}\)
B. \(5\sqrt 2 \;{\rm{cm}}\)
C. \(5\;{\rm{cm}}\)
D. \(\sqrt {10} \;{\rm{cm}}\)
Phần II: Tự luận
Câu 5: Giải hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{3x + 2y = 5}\\{x - 3y = 9}\end{array}} \right.\)
Câu 6: Cho biểu thức \(A = \frac{{x\sqrt x {\rm{ \;}} + 1}}{{x - 1}} - \frac{{x - 1}}{{\sqrt x {\rm{ \;}} + 1}}\) (với \(\left. {x \ge 0;x \ne 1} \right)\).
a) Rút gọn biểu thức \(A\).
b) Tìm tất cả các số nguyên \(x\) để \(A\) nhận giá trị nguyên.
Câu 7: Cho phương trình \({x^2} - \left( {2m + 1} \right)x + {m^2} - 1 = 0\) (1) với \(m\) là tham số.
a) Giải phương trình (1) khi \(m = 5\).
b) Tìm tất cả các giá trị của tham số \(m\) để phương trình (1) có 2 nghiệm \({x_1},{x_2}\) thỏa mãn điều kiện \(\left( {x_1^2 - 2m{x_1} + {m^2}} \right)\left( {{x_2} + 1} \right) = 4.\;\)
Câu 8: Một hãng taxi công nghệ cao có giá cước (giá tiền khách hàng phải trả cho mỗi km) được tính theo các mức như sau:
Mức 1: Giá mở cửa cho \(1\;{\rm{km}}\) đầu tiên là 20000 đồng;
Mức 2: Từ trên \(1\;{\rm{km}}\) đến \(25\;{\rm{km}}\);
Mức 3: Từ trên \(25\;{\rm{km}}\).
Biết rằng anh \({\rm{A}}\) đi \(32\;{\rm{km}}\) phải trả tiền taxi là 479500 đồng còn chị \({\rm{B}}\) đi \(41\;{\rm{km}}\) phải trả 592000 đồng. Hỏi giá cước của hãng taxi trên ở mức 2 và mức 3 là bao nhiêu? Nếu khách hàng đi \(24\;{\rm{km}}\) thì phải trả taxi bao nhiêu tiền?
Câu 9: Cho đường tròn \(\left( O \right)\) và \(BC\) là một dây cung khác đường kính của \(\left( O \right),A\) là điểm di động trên cung lớn \(BC\) sao cho \(AC > AB\left( {A \ne B} \right)\). Gọi \(D\) là chân đường phân giác trong góc \(\widehat {BAC}\) \(\left( {D \in BC} \right)\). Đường thẳng đi qua \(O\) và vuông góc với \(BC\) cắt đường thẳng \(AD\) tại \(E\). Kẻ \(EH,EK\) lần lượt vuông góc với \(AB\) và \(AC\left( {H \in AB,K \in AC} \right)\).
a) Chứng minh \(EHAK\) là tứ giác nội tiếp.
b) Gọi \(F\) là tâm đường tròn nội tiếp tam giác \(ABC\). Chứng minh điểm \(E\) thuộc đường tròn \(\left( O \right)\) và \(E\) là tâm đường tròn ngoại tiếp tam giác \(BCF\).
c) Gọi \(M,N,I\) lần lượt là trung điểm của các đoạn thẳng \(AE,BE\) và \(BC\). Chứng minh \(BMDN\) là tứ giác nội tiếp. Xác định vị trí điểm \(A\) để bốn điểm \(H,N,I,K\) thẳng hàng.
Câu 10: Cho các số thực a, b, c sao cho phương trình \(a{x^2} + bx + c + 2023 = 0\) nhận \(x = 1\)là nghiệm. Tìm giá trị nhỏ nhất của biểu thức:
\(P = \sqrt {3{a^2} - 2ab + 3{b^2}} + \sqrt {5{b^2} - 6bc + 5{c^2}} + \sqrt {6{c^2} - 8ca + 6{a^2}} \)
----- HẾT -----
Phần I: Trắc nghiệm
1.B | 2.A | 3.D | 4.C |
Câu 1 (TH):
Phương pháp:
Biểu thức có nghĩa khi \(120 - 6x \ge 0\).
Cách giải:
Biểu thức \(\sqrt {120 - 6x} \) có nghĩa khi \(120 - 6x \ge 0\) hay \(x \le 20\).
Chọn B.
Câu 2 (NB):
Phương pháp:
Hàm số đồng biến khi a > 0.
Cách giải:
Hàm số \(y = \left( {m - 2023} \right)x + 2024\) đồng biến khi \(m - 2023 > 0\) hay \(m > 2023\).
Chọn A.
Câu 3 (VD):
Phương pháp:
Xét hệ số a + b + c để tìm ra 2 nghiệm của phương trình.
Cách giải:
Phương trình \(3{x^2} - 7x + 4 = 0\) có \(3 + ( - 7) + 4 = 0\) nên phương trình có 2 nghiệm là 1 và \(\frac{4}{3}\).
Khi đó \(\left| {{x_1} - {x_2}} \right| = \left| {1 - \frac{4}{3}} \right| = \frac{1}{3}\)
Chọn D.
Câu 4 (TH):
Phương pháp:
Áp dụng định lí pytago tìm độ dài cạnh còn lại của tam giác ABC. Từ đó tìm được bán kính đường tròn ngoại tiếp bằng một nửa cạnh BC.
Cách giải:
Áp dụng định lí pytago trong tam giác vuông ABC ta có:
\(B{C^2} = A{B^2} + A{C^2}\) hay \(B{C^2} = {6^2} + {8^2} = 100\)Suy ra BC = 10 cm
Vì tam giác ABC vuông tại A nên BC là đường kính của đường tròn ngoại tiếp tam giác ABC.
Vậy bán kính đường tròn ngoại tiếp tam giác ABC là 5 cm.
Chọn C.
Phần II: Tự luận
Câu 5 (TH):
Phương pháp:
Giải hệ phương trình bằng phương pháp cộng đại số hoặc phương pháp thế.
Cách giải:
\(\left\{ {\begin{array}{*{20}{l}}{3x + 2y = 5}\\{x - 3y = 9}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{3x + 2y = 5}\\{3x - 9y = 27}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{11y = {\rm{ \;}} - 22}\\{x = 9 + 3y}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{y = {\rm{ \;}} - 2}\\{x = 3}\end{array}} \right.\)
Vậy hệ phương trình có nghiệm \(\left( {x;y} \right) = \left( {3; - 2} \right)\).
Câu 6 (VD):
Phương pháp:
a) Sử dụng hằng đẳng thức để rút gọn.
b) Tách \(A = 1 + \frac{1}{{\sqrt x {\rm{ \;}} - 1}}\) từ đó tìm x để A nhận giá trị nguyên.
Cách giải:
a) Rút gọn biểu thức \(A\).
\(A = \frac{{x\sqrt x {\rm{ \;}} + 1}}{{x - 1}} - \frac{{x - 1}}{{\sqrt x {\rm{ \;}} + 1}}\)
\(A = \frac{{x\sqrt x {\rm{ \;}} + 1}}{{\left( {\sqrt x {\rm{ \;}} + 1} \right)\left( {\sqrt x {\rm{ \;}} - 1} \right)}} - \frac{{\left( {x - 1} \right)\left( {\sqrt x {\rm{ \;}} - 1} \right)}}{{\left( {\sqrt x {\rm{ \;}} + 1} \right)\left( {\sqrt x {\rm{ \;}} - 1} \right)}}\)
\(A = \frac{{x\sqrt x {\rm{ \;}} + 1 - \left( {x\sqrt x {\rm{ \;}} - x - \sqrt x {\rm{ \;}} + 1} \right)}}{{\left( {\sqrt x {\rm{ \;}} + 1} \right)\left( {\sqrt x {\rm{ \;}} - 1} \right)}}\)
\(A = \frac{{x\sqrt x {\rm{ \;}} + 1 - x\sqrt x {\rm{ \;}} + x + \sqrt x {\rm{ \;}} - 1}}{{\left( {\sqrt x {\rm{ \;}} + 1} \right)\left( {\sqrt x {\rm{ \;}} - 1} \right)}}\)
\(A = \frac{{x + \sqrt x }}{{\left( {\sqrt x {\rm{ \;}} + 1} \right)\left( {\sqrt x {\rm{ \;}} - 1} \right)}}\)
\(A = \frac{{\sqrt x \left( {\sqrt x {\rm{ \;}} + 1} \right)}}{{\left( {\sqrt x {\rm{ \;}} + 1} \right)\left( {\sqrt x {\rm{ \;}} - 1} \right)}}\)
\(A = \frac{{\sqrt x }}{{\sqrt x {\rm{ \;}} - 1}}.\)
Vậy\(A = \frac{{\sqrt x }}{{\sqrt x {\rm{ \;}} - 1}}\)với \(x \ge 0;x \ne 1\).
b) Tìm tất cả các số nguyên \(x\) để \(A\) nhận giá trị nguyên.
Ta có \(A = \frac{{\sqrt x }}{{\sqrt x {\rm{ \;}} - 1}} = \frac{{\sqrt x {\rm{ \;}} - 1 + 1}}{{\sqrt x {\rm{ \;}} - 1}} = 1 + \frac{1}{{\sqrt x {\rm{ \;}} - 1}}\)
Với x nguyên để A nguyên thì \(1 + \frac{1}{{\sqrt x {\rm{ \;}} - 1}} \in \mathbb{Z} \Rightarrow \frac{1}{{\sqrt x {\rm{ \;}} - 1}} \in \mathbb{Z} \Rightarrow \sqrt x {\rm{ \;}} - 1 \in \left\{ { - 1,1} \right\}\)
\(\sqrt x {\rm{ \;}} - 1 = 1 \Leftrightarrow \sqrt x {\rm{ \;}} = 2 \Leftrightarrow x = 4\) (thỏa mãn)
\(\sqrt x {\rm{ \;}} - 1 = {\rm{ \;}} - 1 \Leftrightarrow \sqrt x {\rm{ \;}} = 0 \Leftrightarrow x = 0\) (thỏa mãn)
Vậy \(x \in \left\{ {0,4} \right\}\) thì P nguyên.
Câu 7 (VD):
Phương pháp:
a) Thay m = 5 vào phương trình (1) và thực hiện giải.
b) Áp dụng hệ thức vi-ét \(\left\{ {\begin{array}{*{20}{l}}{{x_1} + {x_2} = {\rm{ \;}} - \frac{b}{a}}\\{{x_1}{x_2} = \frac{c}{a}}\end{array}} \right.\)
Cách giải:
a) Thay m = 5 vào phương trình (1) ta được:
\({x^2} - \left( {2.5 + 1} \right)x + {5^2} - 1 = 0\) \( \Leftrightarrow {x^2} - 11x + 24 = 0{\mkern 1mu} {\mkern 1mu} \)
Ta có \(\Delta {\rm{ \;}} = {\left( { - 11} \right)^2} - 4.1.24 = 25 > 0\) nên phương trình có 2 nghiệm phân biệt \( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = \frac{{11 + \sqrt {25} }}{2} = 8}\\{x = \frac{{11 - \sqrt {25} }}{2} = 3}\end{array}} \right.\)
Vậy với m = 5 phương trình (1) có tập nghiệm \(S = \left\{ {3,8} \right\}\)
b) Ta có \(\Delta {\rm{ \;}} = {\left[ { - \left( {2m + 1} \right)} \right]^2} - 4.1.\left( {{m^2} - 1} \right)\)
\(\begin{array}{*{20}{l}}{ = 4{m^2} + 4m + 1 - 4{m^2} + 4}\\{ = 4m + 5}\end{array}\)
Để phương trình (1) có 2 nghiệm \({x_1},{x_2}\) thì \(\Delta {\rm{ \;}} \ge 0 \Leftrightarrow 4m + 5 \ge 0 \Leftrightarrow m \ge {\rm{ \;}} - \frac{5}{4}\)
Khi đó theo Vi-ét \(\left\{ {\begin{array}{*{20}{l}}{{x_1} + {x_2} = 2m + 1}\\{{x_1}{x_2} = {m^2} - 1}\end{array}} \right.\)
Vì \({x_1}\) là nghiệm của phương trình (1) nên ta có: \({x_1}^2 - \left( {2m + 1} \right){x_1} + {m^2} - 1 = 0{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \)
\( \Leftrightarrow {x_1}^2 - 2m{x_1} + {m^2} = {x_1} + 1\)
Ta có: \(\left( {{x_1}^2 - 2m{x_1} + {m^2}} \right)\left( {{x_2} + 1} \right) = 4\)
\(\begin{array}{*{20}{l}}{ \Leftrightarrow \left( {{x_1} + 1} \right)\left( {{x_2} + 1} \right) = 4}\\{ \Leftrightarrow {x_1}{x_2} + {x_1} + {x_2} + 1 = 4}\\{ \Leftrightarrow {m^2} - 1 + 2m + 1 + 1 = 4}\\{ \Leftrightarrow {m^2} + 2m - 3 = 0}\\{ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{m = 1{\mkern 1mu} {\mkern 1mu} (TM)}\\{m = {\rm{ \;}} - 3{\mkern 1mu} {\mkern 1mu} (KTM)}\end{array}} \right.{\mkern 1mu} }\end{array}\)
Vậy \(m = 1\) là giá trị cần tìm.
Câu 8 (VD):
Phương pháp:
Giải bài toán bằng cách lập hệ phương trình.
Cách giải:
Gọi giá cước của hãng taxi trên ở mức 2 là x (đồng); giá cước của hãng taxi trên ở mức 3 là y (đồng \(\left( {0 \le x,y} \right)\)
Theo đề bài,
Anh A đi 32 km phải trả tiền taxi là 479500 đồng thì anh A phải trả tiền 1 km theo mức 1; trả (25 - 1) = 24 km theo mức 2 và trả (32 – 25) = 7 km theo mức 3 nên ta có phương trình: \(20000{\rm{ }} + {\rm{ }}24x{\rm{ }} + {\rm{ }}7y{\rm{ }} = {\rm{ }}479500 \Leftrightarrow 24x + 7y = 459500\) (1)
Chị B đi 41 km phải trả 592000 đồng thì chị B phải trả tiền 1 km theo mức 1; trả (25 - 1) = 24 km theo mức 2 và trả (41 – 25) = 16 km theo mức 3 nên ta có phương trình:\(20000{\rm{ }} + {\rm{ }}24x{\rm{ }} + {\rm{ }}16y{\rm{ }} = {\rm{ 5920}}00 \Leftrightarrow 24x + 16y = 572000\)(2)
Từ (1) và (2) ta có hệ phương trình:
\(\left\{ \begin{array}{l}24x + 7y = 459500\\24x + 16y = 572000\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}9y = 112500\\24x + 16y = 572000\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}y = 12500\\x = \frac{{572000 - 16.12500}}{{24}}\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}x = 15500\\y = 12500\end{array} \right.\)
Nếu khách hàng đi 24 km thì khách hàng phải trả tiền 1 km theo mức 1; (24 – 1) = 23 km theo mức 2, khi đó số tiền khách hàng phải trả là:
\(20000 + 23.15500 = 376500\)(đồng)
Vậy giá cước của hãng taxi trên ở mức 2 là 15500 đồng, ở mức 3 là 12500 đồng và khách hàng đi 24 km phải trả 376500 đồng.
Câu 9 (VDC):
Cách giải:
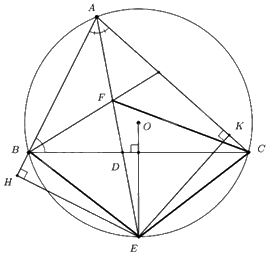
a) Chứng minh EHAK là tứ giác nội tiếp.
Xét tứ giác EHAK có:
\(\begin{array}{*{20}{l}}{\angle AHE = {{90}^0}{\mkern 1mu} {\mkern 1mu} \left( {do{\mkern 1mu} {\mkern 1mu} EH \bot AB} \right)}\\{\angle AKE = {{90}^0}{\mkern 1mu} {\mkern 1mu} \left( {do{\mkern 1mu} {\mkern 1mu} CEK \bot AC} \right)}\\{ \Rightarrow \angle AHE + \angle AKE = {{90}^0} + {{90}^0} = {{180}^0}}\end{array}\)
Mà hai đỉnh H, K là hai đỉnh đối diện nên EHAK là tứ giác nội tiếp (dhnb).
b) Gọi F là tâm đường tròn nội tiếp tam giác ABC. Chứng minh điểm E thuộc đường tròn (O) và E là tâm đường tròn ngoại tiếp tam giác BCF.
Chứng minh điểm E thuộc đường tròn (O).
Vì E thuộc phân giác của góc \(\angle BAC\) nên \(EH = EK\) (tính chất).
Vì OE qua O và vuông góc với BC \( \Rightarrow OE\) đi qua trung điểm của BC (quan hệ vuông góc giữa đường kính và dây cung) \( \Rightarrow EB = EC\) (tính chất).
Xét tam giác vuông EBH và tam giác vuông ECK có:
\(\begin{array}{*{20}{l}}{\angle EHB = \angle EKC = {{90}^0}}\\{EB = EC{\mkern 1mu} {\mkern 1mu} \left( {cmt} \right)}\\{EH = EK{\mkern 1mu} {\mkern 1mu} \left( {cmt} \right)}\end{array}\)
\( \Rightarrow \Delta EBH = \Delta ECK\) (cạnh góc vuông – cạnh huyền)
\( \Rightarrow \angle EBH = \angle ECK = \angle ACE\) (hai góc tương ứng).
Mà \(\angle EBH + \angle ABE = {180^0}\) (kề bù)
\( \Rightarrow \angle ACE + \angle ABE = {180^0}\)
Mà B, C là hai đỉnh đối nhau nên ABEC là tứ giác nội tiếp (dhnb).
Lại có A, B, C cùng thuộc (O) nên ABEC nội tiếp đường tròn (O).
Vậy E thuộc đường tròn (O) (đpcm).
Chứng minh E là tâm đường tròn ngoại tiếp tam giác BCF.
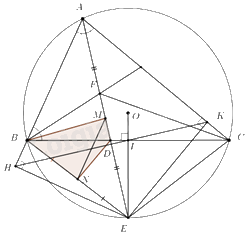
Ta có: \(\angle EBF = \angle EBD + \angle DBF\).
Mà \(\angle EBD = \angle EBC = \angle EAC = \angle BAF\) (hai góc nội tiếp cùng chắn cung EC và AE là phân giác của góc A).
\(\angle DBF = \angle ABF\) (do F là tâm đường nội tiếp tam giác ABC nên BF là phân giác của \(\angle ABC\))
\( \Rightarrow \angle EBF = \angle BAF + \angle ABF = \angle EFB\) (góc ngoài bằng tổng hai góc trong không kề với nó).
\( \Rightarrow \Delta EBF\) cân tại E (định nghĩa) \( \Rightarrow EB = EF\) (tính chất).
Mà \(EB = EC{\mkern 1mu} {\mkern 1mu} \left( {cmt} \right)\) \( \Rightarrow EB = EC = EF\).
Vậy E là tâm đường tròn ngoại tiếp tam giác BCF (đpcm).
Xác định vị trí điểm A để bốn điểm H, N, I, K thẳng hàng.
Xét tứ giác BHEI có: \(\angle BHE + \angle BIE = {90^0} + {90^0} = {180^0}\)
Mà hai đỉnh H, I đối nhau nên BHEI là tứ giác nội tiếp đường tròn tâm N đường kính BE (dhnb)
\( \Rightarrow \angle BIH = \angle BEH\) (hai góc nội tiếp cùng chắn cung BH)
Xét tứ giác CEIK có: \(\angle CIE = \angle CKE = {90^0}\)
Mà I, K kề nhau cùng nhìn EC dưới hai góc bằng nhau nên CEIK là tứ giác nội tiếp (dhnb)
\( \Rightarrow \angle KIC = \angle KEC\) (hai góc nội tiếp cùng chắn cung KC)
Mà \(\Delta EBH = \Delta ECK\) (theo ý b) nên \(\angle BEH = \angle KEC\) (hai góc tương ứng)
\( \Rightarrow \angle BIH = \angle KIC\).
Mà \(\angle BIH + \angle HIC = {180^0}\) (kề bù) \( \Rightarrow \angle KIC + \angle HIC = {180^0} \Rightarrow \angle HIK = {180^0}\)
=> H, I, K thẳng hàng.
Để H, N, I, K thẳng hàng thì cần H, N, I thẳng hàng.
Vì BHEI là tứ giác nội tiếp đường tròn tâm N đường kính BE (cmt) nên NH = NI.
Mà H, N, I thẳng hàng => N là trung điểm của HI.
Mà N lại là trung điểm của BE
=> BHEI là hình bình hành (dhnb).
Lại có \(\angle BHE = {90^0}{\mkern 1mu} {\mkern 1mu} \left( {gt} \right)\) => BHEI là hình chữ nhật (dhnb)
\( \Rightarrow \angle HBI = {90^0} \Rightarrow \angle ABC = {90^0}\).
\( \Rightarrow \Delta ABC\) vuông tại B.
Vậy A nằm trên đường tròn (O) sao cho \(\Delta ABC\) vuông tại B.
Câu 10 (VDC):
Cách giải:
Phương trình \(a{x^2} + bx + c + 2023 = 0\) nhận \(x = 1\) là nghiệm nên ta có: \(a + b + c + 2023 = 0 \Leftrightarrow a + b + c = - 2023\)
Với mọi \(a,b,c \in \mathbb{R}\) ta có: \({\left( {a - b} \right)^2} \ge 0;\,\,{\left( {b - c} \right)^2} \ge 0;\,\,{\left( {c - a} \right)^2} \ge 0\)
Khi đó:
\(\begin{array}{l}P = \sqrt {{{\left( {a + b} \right)}^2} + 2{{\left( {a - b} \right)}^2}} + \sqrt {{{\left( {b + c} \right)}^2} + 4{{\left( {b - c} \right)}^2}} + \sqrt {{{\left( {c + a} \right)}^2} + 5{{\left( {c - a} \right)}^2}} \\\,\,\,\,\, \ge \sqrt {{{\left( {a + b} \right)}^2}} + \sqrt {{{\left( {b + c} \right)}^2}} + \sqrt {{{\left( {c + a} \right)}^2}} \\\,\,\,\,\, = \left| {a + b} \right| + \left| {b + c} \right| + \left| {c + a} \right|\\\,\,\,\,\, \ge \left| {2\left( {a + b + c} \right)} \right| = 2.2023 = 4046\end{array}\)
Dấu “=” xảy ra khi và chỉ khi \(a = b = c = \frac{{ - 2023}}{3}\)
Vậy giá trị nhỏ nhất của P là 4046 khi \(a = b = c = \frac{{ - 2023}}{3}\).
-----HẾT-----
Phần I: Trắc nghiệm
1.B | 2.A | 3.D | 4.C |
Câu 1 (TH):
Phương pháp:
Biểu thức có nghĩa khi \(120 - 6x \ge 0\).
Cách giải:
Biểu thức \(\sqrt {120 - 6x} \) có nghĩa khi \(120 - 6x \ge 0\) hay \(x \le 20\).
Chọn B.
Câu 2 (NB):
Phương pháp:
Hàm số đồng biến khi a > 0.
Cách giải:
Hàm số \(y = \left( {m - 2023} \right)x + 2024\) đồng biến khi \(m - 2023 > 0\) hay \(m > 2023\).
Chọn A.
Câu 3 (VD):
Phương pháp:
Xét hệ số a + b + c để tìm ra 2 nghiệm của phương trình.
Cách giải:
Phương trình \(3{x^2} - 7x + 4 = 0\) có \(3 + ( - 7) + 4 = 0\) nên phương trình có 2 nghiệm là 1 và \(\frac{4}{3}\).
Khi đó \(\left| {{x_1} - {x_2}} \right| = \left| {1 - \frac{4}{3}} \right| = \frac{1}{3}\)
Chọn D.
Câu 4 (TH):
Phương pháp:
Áp dụng định lí pytago tìm độ dài cạnh còn lại của tam giác ABC. Từ đó tìm được bán kính đường tròn ngoại tiếp bằng một nửa cạnh BC.
Cách giải:
Áp dụng định lí pytago trong tam giác vuông ABC ta có:
\(B{C^2} = A{B^2} + A{C^2}\) hay \(B{C^2} = {6^2} + {8^2} = 100\)Suy ra BC = 10 cm
Vì tam giác ABC vuông tại A nên BC là đường kính của đường tròn ngoại tiếp tam giác ABC.
Vậy bán kính đường tròn ngoại tiếp tam giác ABC là 5 cm.
Chọn C.
Phần II: Tự luận
Câu 5 (TH):
Phương pháp:
Giải hệ phương trình bằng phương pháp cộng đại số hoặc phương pháp thế.
Cách giải:
\(\left\{ {\begin{array}{*{20}{l}}{3x + 2y = 5}\\{x - 3y = 9}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{3x + 2y = 5}\\{3x - 9y = 27}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{11y = {\rm{ \;}} - 22}\\{x = 9 + 3y}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{y = {\rm{ \;}} - 2}\\{x = 3}\end{array}} \right.\)
Vậy hệ phương trình có nghiệm \(\left( {x;y} \right) = \left( {3; - 2} \right)\).
Câu 6 (VD):
Phương pháp:
a) Sử dụng hằng đẳng thức để rút gọn.
b) Tách \(A = 1 + \frac{1}{{\sqrt x {\rm{ \;}} - 1}}\) từ đó tìm x để A nhận giá trị nguyên.
Cách giải:
a) Rút gọn biểu thức \(A\).
\(A = \frac{{x\sqrt x {\rm{ \;}} + 1}}{{x - 1}} - \frac{{x - 1}}{{\sqrt x {\rm{ \;}} + 1}}\)
\(A = \frac{{x\sqrt x {\rm{ \;}} + 1}}{{\left( {\sqrt x {\rm{ \;}} + 1} \right)\left( {\sqrt x {\rm{ \;}} - 1} \right)}} - \frac{{\left( {x - 1} \right)\left( {\sqrt x {\rm{ \;}} - 1} \right)}}{{\left( {\sqrt x {\rm{ \;}} + 1} \right)\left( {\sqrt x {\rm{ \;}} - 1} \right)}}\)
\(A = \frac{{x\sqrt x {\rm{ \;}} + 1 - \left( {x\sqrt x {\rm{ \;}} - x - \sqrt x {\rm{ \;}} + 1} \right)}}{{\left( {\sqrt x {\rm{ \;}} + 1} \right)\left( {\sqrt x {\rm{ \;}} - 1} \right)}}\)
\(A = \frac{{x\sqrt x {\rm{ \;}} + 1 - x\sqrt x {\rm{ \;}} + x + \sqrt x {\rm{ \;}} - 1}}{{\left( {\sqrt x {\rm{ \;}} + 1} \right)\left( {\sqrt x {\rm{ \;}} - 1} \right)}}\)
\(A = \frac{{x + \sqrt x }}{{\left( {\sqrt x {\rm{ \;}} + 1} \right)\left( {\sqrt x {\rm{ \;}} - 1} \right)}}\)
\(A = \frac{{\sqrt x \left( {\sqrt x {\rm{ \;}} + 1} \right)}}{{\left( {\sqrt x {\rm{ \;}} + 1} \right)\left( {\sqrt x {\rm{ \;}} - 1} \right)}}\)
\(A = \frac{{\sqrt x }}{{\sqrt x {\rm{ \;}} - 1}}.\)
Vậy\(A = \frac{{\sqrt x }}{{\sqrt x {\rm{ \;}} - 1}}\)với \(x \ge 0;x \ne 1\).
b) Tìm tất cả các số nguyên \(x\) để \(A\) nhận giá trị nguyên.
Ta có \(A = \frac{{\sqrt x }}{{\sqrt x {\rm{ \;}} - 1}} = \frac{{\sqrt x {\rm{ \;}} - 1 + 1}}{{\sqrt x {\rm{ \;}} - 1}} = 1 + \frac{1}{{\sqrt x {\rm{ \;}} - 1}}\)
Với x nguyên để A nguyên thì \(1 + \frac{1}{{\sqrt x {\rm{ \;}} - 1}} \in \mathbb{Z} \Rightarrow \frac{1}{{\sqrt x {\rm{ \;}} - 1}} \in \mathbb{Z} \Rightarrow \sqrt x {\rm{ \;}} - 1 \in \left\{ { - 1,1} \right\}\)
\(\sqrt x {\rm{ \;}} - 1 = 1 \Leftrightarrow \sqrt x {\rm{ \;}} = 2 \Leftrightarrow x = 4\) (thỏa mãn)
\(\sqrt x {\rm{ \;}} - 1 = {\rm{ \;}} - 1 \Leftrightarrow \sqrt x {\rm{ \;}} = 0 \Leftrightarrow x = 0\) (thỏa mãn)
Vậy \(x \in \left\{ {0,4} \right\}\) thì P nguyên.
Câu 7 (VD):
Phương pháp:
a) Thay m = 5 vào phương trình (1) và thực hiện giải.
b) Áp dụng hệ thức vi-ét \(\left\{ {\begin{array}{*{20}{l}}{{x_1} + {x_2} = {\rm{ \;}} - \frac{b}{a}}\\{{x_1}{x_2} = \frac{c}{a}}\end{array}} \right.\)
Cách giải:
a) Thay m = 5 vào phương trình (1) ta được:
\({x^2} - \left( {2.5 + 1} \right)x + {5^2} - 1 = 0\) \( \Leftrightarrow {x^2} - 11x + 24 = 0{\mkern 1mu} {\mkern 1mu} \)
Ta có \(\Delta {\rm{ \;}} = {\left( { - 11} \right)^2} - 4.1.24 = 25 > 0\) nên phương trình có 2 nghiệm phân biệt \( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = \frac{{11 + \sqrt {25} }}{2} = 8}\\{x = \frac{{11 - \sqrt {25} }}{2} = 3}\end{array}} \right.\)
Vậy với m = 5 phương trình (1) có tập nghiệm \(S = \left\{ {3,8} \right\}\)
b) Ta có \(\Delta {\rm{ \;}} = {\left[ { - \left( {2m + 1} \right)} \right]^2} - 4.1.\left( {{m^2} - 1} \right)\)
\(\begin{array}{*{20}{l}}{ = 4{m^2} + 4m + 1 - 4{m^2} + 4}\\{ = 4m + 5}\end{array}\)
Để phương trình (1) có 2 nghiệm \({x_1},{x_2}\) thì \(\Delta {\rm{ \;}} \ge 0 \Leftrightarrow 4m + 5 \ge 0 \Leftrightarrow m \ge {\rm{ \;}} - \frac{5}{4}\)
Khi đó theo Vi-ét \(\left\{ {\begin{array}{*{20}{l}}{{x_1} + {x_2} = 2m + 1}\\{{x_1}{x_2} = {m^2} - 1}\end{array}} \right.\)
Vì \({x_1}\) là nghiệm của phương trình (1) nên ta có: \({x_1}^2 - \left( {2m + 1} \right){x_1} + {m^2} - 1 = 0{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \)
\( \Leftrightarrow {x_1}^2 - 2m{x_1} + {m^2} = {x_1} + 1\)
Ta có: \(\left( {{x_1}^2 - 2m{x_1} + {m^2}} \right)\left( {{x_2} + 1} \right) = 4\)
\(\begin{array}{*{20}{l}}{ \Leftrightarrow \left( {{x_1} + 1} \right)\left( {{x_2} + 1} \right) = 4}\\{ \Leftrightarrow {x_1}{x_2} + {x_1} + {x_2} + 1 = 4}\\{ \Leftrightarrow {m^2} - 1 + 2m + 1 + 1 = 4}\\{ \Leftrightarrow {m^2} + 2m - 3 = 0}\\{ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{m = 1{\mkern 1mu} {\mkern 1mu} (TM)}\\{m = {\rm{ \;}} - 3{\mkern 1mu} {\mkern 1mu} (KTM)}\end{array}} \right.{\mkern 1mu} }\end{array}\)
Vậy \(m = 1\) là giá trị cần tìm.
Câu 8 (VD):
Phương pháp:
Giải bài toán bằng cách lập hệ phương trình.
Cách giải:
Gọi giá cước của hãng taxi trên ở mức 2 là x (đồng); giá cước của hãng taxi trên ở mức 3 là y (đồng \(\left( {0 \le x,y} \right)\)
Theo đề bài,
Anh A đi 32 km phải trả tiền taxi là 479500 đồng thì anh A phải trả tiền 1 km theo mức 1; trả (25 - 1) = 24 km theo mức 2 và trả (32 – 25) = 7 km theo mức 3 nên ta có phương trình: \(20000{\rm{ }} + {\rm{ }}24x{\rm{ }} + {\rm{ }}7y{\rm{ }} = {\rm{ }}479500 \Leftrightarrow 24x + 7y = 459500\) (1)
Chị B đi 41 km phải trả 592000 đồng thì chị B phải trả tiền 1 km theo mức 1; trả (25 - 1) = 24 km theo mức 2 và trả (41 – 25) = 16 km theo mức 3 nên ta có phương trình:\(20000{\rm{ }} + {\rm{ }}24x{\rm{ }} + {\rm{ }}16y{\rm{ }} = {\rm{ 5920}}00 \Leftrightarrow 24x + 16y = 572000\)(2)
Từ (1) và (2) ta có hệ phương trình:
\(\left\{ \begin{array}{l}24x + 7y = 459500\\24x + 16y = 572000\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}9y = 112500\\24x + 16y = 572000\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}y = 12500\\x = \frac{{572000 - 16.12500}}{{24}}\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}x = 15500\\y = 12500\end{array} \right.\)
Nếu khách hàng đi 24 km thì khách hàng phải trả tiền 1 km theo mức 1; (24 – 1) = 23 km theo mức 2, khi đó số tiền khách hàng phải trả là:
\(20000 + 23.15500 = 376500\)(đồng)
Vậy giá cước của hãng taxi trên ở mức 2 là 15500 đồng, ở mức 3 là 12500 đồng và khách hàng đi 24 km phải trả 376500 đồng.
Câu 9 (VDC):
Cách giải:
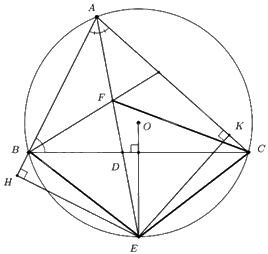
a) Chứng minh EHAK là tứ giác nội tiếp.
Xét tứ giác EHAK có:
\(\begin{array}{*{20}{l}}{\angle AHE = {{90}^0}{\mkern 1mu} {\mkern 1mu} \left( {do{\mkern 1mu} {\mkern 1mu} EH \bot AB} \right)}\\{\angle AKE = {{90}^0}{\mkern 1mu} {\mkern 1mu} \left( {do{\mkern 1mu} {\mkern 1mu} CEK \bot AC} \right)}\\{ \Rightarrow \angle AHE + \angle AKE = {{90}^0} + {{90}^0} = {{180}^0}}\end{array}\)
Mà hai đỉnh H, K là hai đỉnh đối diện nên EHAK là tứ giác nội tiếp (dhnb).
b) Gọi F là tâm đường tròn nội tiếp tam giác ABC. Chứng minh điểm E thuộc đường tròn (O) và E là tâm đường tròn ngoại tiếp tam giác BCF.
Chứng minh điểm E thuộc đường tròn (O).
Vì E thuộc phân giác của góc \(\angle BAC\) nên \(EH = EK\) (tính chất).
Vì OE qua O và vuông góc với BC \( \Rightarrow OE\) đi qua trung điểm của BC (quan hệ vuông góc giữa đường kính và dây cung) \( \Rightarrow EB = EC\) (tính chất).
Xét tam giác vuông EBH và tam giác vuông ECK có:
\(\begin{array}{*{20}{l}}{\angle EHB = \angle EKC = {{90}^0}}\\{EB = EC{\mkern 1mu} {\mkern 1mu} \left( {cmt} \right)}\\{EH = EK{\mkern 1mu} {\mkern 1mu} \left( {cmt} \right)}\end{array}\)
\( \Rightarrow \Delta EBH = \Delta ECK\) (cạnh góc vuông – cạnh huyền)
\( \Rightarrow \angle EBH = \angle ECK = \angle ACE\) (hai góc tương ứng).
Mà \(\angle EBH + \angle ABE = {180^0}\) (kề bù)
\( \Rightarrow \angle ACE + \angle ABE = {180^0}\)
Mà B, C là hai đỉnh đối nhau nên ABEC là tứ giác nội tiếp (dhnb).
Lại có A, B, C cùng thuộc (O) nên ABEC nội tiếp đường tròn (O).
Vậy E thuộc đường tròn (O) (đpcm).
Chứng minh E là tâm đường tròn ngoại tiếp tam giác BCF.
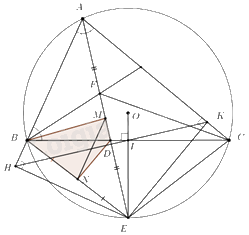
Ta có: \(\angle EBF = \angle EBD + \angle DBF\).
Mà \(\angle EBD = \angle EBC = \angle EAC = \angle BAF\) (hai góc nội tiếp cùng chắn cung EC và AE là phân giác của góc A).
\(\angle DBF = \angle ABF\) (do F là tâm đường nội tiếp tam giác ABC nên BF là phân giác của \(\angle ABC\))
\( \Rightarrow \angle EBF = \angle BAF + \angle ABF = \angle EFB\) (góc ngoài bằng tổng hai góc trong không kề với nó).
\( \Rightarrow \Delta EBF\) cân tại E (định nghĩa) \( \Rightarrow EB = EF\) (tính chất).
Mà \(EB = EC{\mkern 1mu} {\mkern 1mu} \left( {cmt} \right)\) \( \Rightarrow EB = EC = EF\).
Vậy E là tâm đường tròn ngoại tiếp tam giác BCF (đpcm).
Xác định vị trí điểm A để bốn điểm H, N, I, K thẳng hàng.
Xét tứ giác BHEI có: \(\angle BHE + \angle BIE = {90^0} + {90^0} = {180^0}\)
Mà hai đỉnh H, I đối nhau nên BHEI là tứ giác nội tiếp đường tròn tâm N đường kính BE (dhnb)
\( \Rightarrow \angle BIH = \angle BEH\) (hai góc nội tiếp cùng chắn cung BH)
Xét tứ giác CEIK có: \(\angle CIE = \angle CKE = {90^0}\)
Mà I, K kề nhau cùng nhìn EC dưới hai góc bằng nhau nên CEIK là tứ giác nội tiếp (dhnb)
\( \Rightarrow \angle KIC = \angle KEC\) (hai góc nội tiếp cùng chắn cung KC)
Mà \(\Delta EBH = \Delta ECK\) (theo ý b) nên \(\angle BEH = \angle KEC\) (hai góc tương ứng)
\( \Rightarrow \angle BIH = \angle KIC\).
Mà \(\angle BIH + \angle HIC = {180^0}\) (kề bù) \( \Rightarrow \angle KIC + \angle HIC = {180^0} \Rightarrow \angle HIK = {180^0}\)
=> H, I, K thẳng hàng.
Để H, N, I, K thẳng hàng thì cần H, N, I thẳng hàng.
Vì BHEI là tứ giác nội tiếp đường tròn tâm N đường kính BE (cmt) nên NH = NI.
Mà H, N, I thẳng hàng => N là trung điểm của HI.
Mà N lại là trung điểm của BE
=> BHEI là hình bình hành (dhnb).
Lại có \(\angle BHE = {90^0}{\mkern 1mu} {\mkern 1mu} \left( {gt} \right)\) => BHEI là hình chữ nhật (dhnb)
\( \Rightarrow \angle HBI = {90^0} \Rightarrow \angle ABC = {90^0}\).
\( \Rightarrow \Delta ABC\) vuông tại B.
Vậy A nằm trên đường tròn (O) sao cho \(\Delta ABC\) vuông tại B.
Câu 10 (VDC):
Cách giải:
Phương trình \(a{x^2} + bx + c + 2023 = 0\) nhận \(x = 1\) là nghiệm nên ta có: \(a + b + c + 2023 = 0 \Leftrightarrow a + b + c = - 2023\)
Với mọi \(a,b,c \in \mathbb{R}\) ta có: \({\left( {a - b} \right)^2} \ge 0;\,\,{\left( {b - c} \right)^2} \ge 0;\,\,{\left( {c - a} \right)^2} \ge 0\)
Khi đó:
\(\begin{array}{l}P = \sqrt {{{\left( {a + b} \right)}^2} + 2{{\left( {a - b} \right)}^2}} + \sqrt {{{\left( {b + c} \right)}^2} + 4{{\left( {b - c} \right)}^2}} + \sqrt {{{\left( {c + a} \right)}^2} + 5{{\left( {c - a} \right)}^2}} \\\,\,\,\,\, \ge \sqrt {{{\left( {a + b} \right)}^2}} + \sqrt {{{\left( {b + c} \right)}^2}} + \sqrt {{{\left( {c + a} \right)}^2}} \\\,\,\,\,\, = \left| {a + b} \right| + \left| {b + c} \right| + \left| {c + a} \right|\\\,\,\,\,\, \ge \left| {2\left( {a + b + c} \right)} \right| = 2.2023 = 4046\end{array}\)
Dấu “=” xảy ra khi và chỉ khi \(a = b = c = \frac{{ - 2023}}{3}\)
Vậy giá trị nhỏ nhất của P là 4046 khi \(a = b = c = \frac{{ - 2023}}{3}\).
-----HẾT-----
Kỳ thi tuyển sinh vào lớp 10 môn Toán Vĩnh Phúc năm 2023 là một bước ngoặt quan trọng trong quá trình học tập của các em học sinh. Đề thi thường bao gồm các dạng bài tập thuộc nhiều chủ đề khác nhau, đòi hỏi học sinh phải có kiến thức vững chắc và kỹ năng giải quyết vấn đề tốt. Việc nắm vững cấu trúc đề thi, các dạng bài tập thường gặp và phương pháp giải quyết hiệu quả là chìa khóa để đạt kết quả cao trong kỳ thi này.
Thông thường, đề thi vào 10 môn Toán Vĩnh Phúc 2023 có cấu trúc gồm hai phần chính:
Để giải đề thi vào 10 môn Toán Vĩnh Phúc 2023 hiệu quả, các em học sinh cần:
Giaitoan.edu.vn cung cấp một nền tảng học toán online hiện đại và hiệu quả, giúp các em học sinh:
Trong quá trình ôn thi, các em học sinh cần:
Đề thi vào 10 môn Toán Vĩnh Phúc năm 2023 là một thử thách lớn, nhưng với sự chuẩn bị kỹ lưỡng và phương pháp học tập hiệu quả, các em học sinh hoàn toàn có thể đạt được kết quả tốt nhất. Giaitoan.edu.vn hy vọng sẽ là người bạn đồng hành đáng tin cậy trên con đường chinh phục kỳ thi này.