Giaitoan.edu.vn xin giới thiệu bộ đề thi tuyển sinh vào lớp 10 môn Toán tỉnh Kiên Giang năm 2021. Đây là tài liệu vô cùng quan trọng giúp các em học sinh làm quen với cấu trúc đề thi, rèn luyện kỹ năng giải toán và tự tin hơn trong kỳ thi sắp tới.
Bộ đề thi này bao gồm các đề thi chính thức của kỳ thi tuyển sinh vào lớp 10 năm 2021 tại tỉnh Kiên Giang, được chúng tôi tổng hợp và cung cấp hoàn toàn miễn phí.
I. PHẦN TRẮC NGHIỆM (3,0 điểm; gồm 15 câu hỏi trắc nghiệm một lựa chọn)
I. PHẦN TRẮC NGHIỆM (3,0 điểm; gồm 15 câu hỏi trắc nghiệm một lựa chọn) Thí sinh kẻ bẳng sau đây vào giấy thi và điền đáp án của câu hỏi vào ô tương ứng.
Câu | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
Đáp án |
Câu 1. Giá trị của biểu thức \(\dfrac{{\sqrt {128} }}{{\sqrt 8 }}\) bằng:
A. \(16\)B. \(8\) C. \(\sqrt 2 \) D. \(4\)
Câu 2. Giá trị của hàm số \(y = \dfrac{1}{3}{x^2}\) tại điểm \(x = - 3\) là:
A. \( - 3\)B. \(3\) C. \(9\) D. \( - 9\)
Câu 3. Biệt thức của phương trình \({x^2} - 3x - 1 = 0\) là:
A. \(\Delta = 5\)B. \(\Delta = 13\) C. \(\Delta = - 5\) D. \(\Delta = - 13\)
Câu 4. Phương trình \({x^2} + 2x - 3 = 0\) có tập nghiệm là:
A. \(S = \left\{ {1;3} \right\}\)B. \(S = \left\{ {1; - 3} \right\}\) C. \(S = \left\{ { - 1; - 3} \right\}\) D. \(S = \left\{ { - 1;3} \right\}\)
Câu 5. Điểm nào sau đây thuộc đồ thị hàm số \(y = 5x + 2?\)
A. \(M\left( {5;2} \right)\)B. \(P\left( {2;0} \right)\) C. \(N\left( {1;7} \right)\) D. \(Q\left( { - \dfrac{5}{2};0} \right)\)
Câu 6. Nếu đường tròn có bán kính bằng \(3\) thì đường tròn đó có chu vi bằng:
A. \(2\pi \)B. \(9\pi \) C. \(6\pi \) D. \(3\pi \)
Câu 7. Nghiệm của hệ phương trình \(\left\{ \begin{array}{l}3x + y = 9\\2x + y = 7\end{array} \right.\) là:
A. \(\left( {2;3} \right)\)B. \(\left( {3;2} \right)\) C. \(\left( { - 2; - 3} \right)\) D. \(\left( { - 3; - 2} \right)\)
Câu 8. Trong các hàm số sau, hàm số nào đồng biến trên \(\mathbb{R}?\)
A. \(y = - x + 1\)B. \(y = - 2x + 1\) C. \(y = - \sqrt 3 x + 2\) D. \(y = x + 2\)
Câu 9. Một hình nón có bán kính đáy bằng \(3\left( {cm} \right)\) và chiều cao bằng \(2\left( {cm} \right)\). Thể tích của hình nón bằng:
A. \(12\pi \left( {c{m^3}} \right)\)B. \(6\pi \left( {c{m^3}} \right)\) C. \(2\pi \left( {c{m^3}} \right)\) D. \(18\pi \left( {c{m^3}} \right)\)
Câu 10. Hai đường thẳng \({d_1}:y = x + 2\) và \({d_2}:y = ax + 3\) song song với nhau khi
A. \(a \ne 1\)B. \(a = 1\) C. \(a = - 1\) D. \(a \ne - 1\)
Câu 11. Biểu thức \(\sqrt {2x - 2} \) có nghĩa khi:
A. \(x \ge 1\)B. \(x \le 1\) C. \(x \le - 1\) D. \(x \ge - 1\)
Câu 12. Nếu phương trình bậc hai \({x^2} + bx + c = 0\) có hai nghiệm là \(x = 2\) và \(x = - 3\) thì \(b + c\) bằng:
A. \( - 6\)B. \(5\) C. \( - 5\) D. \(3\)
Câu 13. Cho tam giác \(ABC\) vuông tại \(A\). Gọi \(H\) là chân đường cao đỉnh \(A\) của tam giác \(ABC\), \(BH = 2cm,\)\(CH = 3cm\), độ dài của đoạn \(AH\) bằng bao nhiêu?
A. \(\sqrt 5 cm\)B. \(6cm\) C. \(1cm\) D. \(\sqrt 6 cm\)
Câu 14. Tính diện tích xung quanh của hình trụ có đường kính đáy \(8\left( {cm} \right)\) và chiều cao \(12\left( {cm} \right)\)
A. \(96\pi \left( {c{m^2}} \right)\)B. \(128\pi \left( {c{m^2}} \right)\) C. \(48\pi \left( {c{m^2}} \right)\) D. \(192\pi \left( {c{m^2}} \right)\)
Câu 15. (ID: 555540) Mặt cầu \(\left( S \right)\) có độ dài đường kính bằng \(d\). Diện tích của mặt cầu \(\left( S \right)\) là:
A. \(4\pi {d^2}\)B. \(\pi {d^2}\) C. \(2\pi {d^2}\) D. \(\dfrac{1}{4}\pi {d^2}\)
II. TỰ LUẬN (7,0 điểm, gồm 5 bài toán)
Bài 1. (1,5 điểm)
a) (ID: 555541) Thực hiện phép tính \(A = \sqrt {112} - \sqrt {63} \)
b) (ID: 555542) Rút gọn biểu thức \(B = \left( {\dfrac{{x - 4}}{{\sqrt x + 2}} - 2\sqrt x } \right):\dfrac{1}{{\left( {\sqrt x - 2} \right)}}\) với \(x \ge 0,\,\,x \ne 4.\)
Bài 2 (1,5 điểm):
a) Vẽ Parabol \(\left( P \right):y = \dfrac{1}{2}{x^2}\) trên trục tọa độ \(Oxy\)
b) Tìm tham số \(m\) để đường thẳng \(\left( d \right):y = 2x + m\) cắt \(\left( P \right)\) tại hai điểm phân biệt.
Bài 3. (1,5 điểm)
a) (ID: 555544) Cho phương trình \(2{x^2} + 4x + m = 0\) (\(m\) là tham số). Tìm tất cả các giá trị của \(m\) để phương trình đã cho có hai nghiệm \({x_1},\,\,{x_2}\) thỏa mãn \(x_1^2 + x_2^2 = 10\).
b) (ID: 555545) Theo kế hoạch, công an tỉnh Kiên Giang điều 2 tổ công tác đến làm thẻ Căn cước công dân cho một phường trên địa bàn thành phố Rạch Giá. Nếu cả 2 tổ cùng làm thì trong 4 ngày hoàn thành công việc, Nếu mỗi tổ làm riêng thì thời gian hoàn thành của tổ I ít hơn thời gian hoàn thành của tố II là 6 ngày. Hỏi nếu làm riêng thì mỗi tổ phải làm trong bao nhiêu ngày để hoàn thành công việc?
Bài 4. (2,0 điểm)
Cho hai đường tròn \(\left( {O;R} \right)\) và \(\left( {O';r} \right)\) tiếp xúc ngoài tại \(A\,\,\left( {R > r} \right)\). Gọi \(BC\) là tiếp tuyến chung ngoài của hai đường tròn này (với \(B \in \left( O \right)\) và \(C \in \left( {O'} \right)\)). Tiếp tuyến chung tại \(A\) của hai đường tròn \(\left( O \right)\) và \(\left( {O'} \right)\) cắt đoạn thẳng \(BC\) tại \(M\).
a) Chứng minh \(OM\) vuông góc với \(O'M\).
b) Gọi \(E\) là giao điểm của \(AB\) với \(OM\) và \(F\) là giao điểm của \(AC\) với \(O'M\). Chứng minh tứ giác \(OEFO'\) nội tiếp một đường tròn.
c) Gọi \(I\) là tâm đường tròn ngoại tiếp tứ giác \(OEFO'\), \(K\) là trung điểm của đoạn \(AM\). Chứng minh \(OO' = 2IK\).
Bài 5 (1,5 điểm)
Các ăng ten parabol thu sóng hoạt động dựa theo nguyên lý: mọi tia sóng song song với trục của parabol đều có tia phản xạ đi qua tiêu điểm \(F\) của parabol (vì vậy nếu ta đặt thiết bị thu sóng tại \(F\) thì sẽ thu sóng được tốt nhất). Người ta chứng minh được rằng: Nếu đường thẳng vuông góc với trục của parabol tại \(F\) cắt parabol tại 2 điểm \(A,B\) thì \(OF = \dfrac{1}{4}AB\) với \(O\) là đỉnh của parabol (tham khảo hình vẽ).
Tính độ dài đoạn \(OF\)ứng với mô hình trên của một ăng ten parabol (ngang 90cm và cao 9 cm).
I. PHẦN TRẮC NGHIỆM (3,0 điểm; gồm 15 câu hỏi trắc nghiệm một lựa chọn) Thí sinh kẻ bẳng sau đây vào giấy thi và điền đáp án của câu hỏi vào ô tương ứng.
Câu | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
Đáp án |
Câu 1. Giá trị của biểu thức \(\dfrac{{\sqrt {128} }}{{\sqrt 8 }}\) bằng:
A. \(16\)B. \(8\) C. \(\sqrt 2 \) D. \(4\)
Câu 2. Giá trị của hàm số \(y = \dfrac{1}{3}{x^2}\) tại điểm \(x = - 3\) là:
A. \( - 3\)B. \(3\) C. \(9\) D. \( - 9\)
Câu 3. Biệt thức của phương trình \({x^2} - 3x - 1 = 0\) là:
A. \(\Delta = 5\)B. \(\Delta = 13\) C. \(\Delta = - 5\) D. \(\Delta = - 13\)
Câu 4. Phương trình \({x^2} + 2x - 3 = 0\) có tập nghiệm là:
A. \(S = \left\{ {1;3} \right\}\)B. \(S = \left\{ {1; - 3} \right\}\) C. \(S = \left\{ { - 1; - 3} \right\}\) D. \(S = \left\{ { - 1;3} \right\}\)
Câu 5. Điểm nào sau đây thuộc đồ thị hàm số \(y = 5x + 2?\)
A. \(M\left( {5;2} \right)\)B. \(P\left( {2;0} \right)\) C. \(N\left( {1;7} \right)\) D. \(Q\left( { - \dfrac{5}{2};0} \right)\)
Câu 6. Nếu đường tròn có bán kính bằng \(3\) thì đường tròn đó có chu vi bằng:
A. \(2\pi \)B. \(9\pi \) C. \(6\pi \) D. \(3\pi \)
Câu 7. Nghiệm của hệ phương trình \(\left\{ \begin{array}{l}3x + y = 9\\2x + y = 7\end{array} \right.\) là:
A. \(\left( {2;3} \right)\)B. \(\left( {3;2} \right)\) C. \(\left( { - 2; - 3} \right)\) D. \(\left( { - 3; - 2} \right)\)
Câu 8. Trong các hàm số sau, hàm số nào đồng biến trên \(\mathbb{R}?\)
A. \(y = - x + 1\)B. \(y = - 2x + 1\) C. \(y = - \sqrt 3 x + 2\) D. \(y = x + 2\)
Câu 9. Một hình nón có bán kính đáy bằng \(3\left( {cm} \right)\) và chiều cao bằng \(2\left( {cm} \right)\). Thể tích của hình nón bằng:
A. \(12\pi \left( {c{m^3}} \right)\)B. \(6\pi \left( {c{m^3}} \right)\) C. \(2\pi \left( {c{m^3}} \right)\) D. \(18\pi \left( {c{m^3}} \right)\)
Câu 10. Hai đường thẳng \({d_1}:y = x + 2\) và \({d_2}:y = ax + 3\) song song với nhau khi
A. \(a \ne 1\)B. \(a = 1\) C. \(a = - 1\) D. \(a \ne - 1\)
Câu 11. Biểu thức \(\sqrt {2x - 2} \) có nghĩa khi:
A. \(x \ge 1\)B. \(x \le 1\) C. \(x \le - 1\) D. \(x \ge - 1\)
Câu 12. Nếu phương trình bậc hai \({x^2} + bx + c = 0\) có hai nghiệm là \(x = 2\) và \(x = - 3\) thì \(b + c\) bằng:
A. \( - 6\)B. \(5\) C. \( - 5\) D. \(3\)
Câu 13. Cho tam giác \(ABC\) vuông tại \(A\). Gọi \(H\) là chân đường cao đỉnh \(A\) của tam giác \(ABC\), \(BH = 2cm,\)\(CH = 3cm\), độ dài của đoạn \(AH\) bằng bao nhiêu?
A. \(\sqrt 5 cm\)B. \(6cm\) C. \(1cm\) D. \(\sqrt 6 cm\)
Câu 14. Tính diện tích xung quanh của hình trụ có đường kính đáy \(8\left( {cm} \right)\) và chiều cao \(12\left( {cm} \right)\)
A. \(96\pi \left( {c{m^2}} \right)\)B. \(128\pi \left( {c{m^2}} \right)\) C. \(48\pi \left( {c{m^2}} \right)\) D. \(192\pi \left( {c{m^2}} \right)\)
Câu 15. (ID: 555540) Mặt cầu \(\left( S \right)\) có độ dài đường kính bằng \(d\). Diện tích của mặt cầu \(\left( S \right)\) là:
A. \(4\pi {d^2}\)B. \(\pi {d^2}\) C. \(2\pi {d^2}\) D. \(\dfrac{1}{4}\pi {d^2}\)
II. TỰ LUẬN (7,0 điểm, gồm 5 bài toán)
Bài 1. (1,5 điểm)
a) (ID: 555541) Thực hiện phép tính \(A = \sqrt {112} - \sqrt {63} \)
b) (ID: 555542) Rút gọn biểu thức \(B = \left( {\dfrac{{x - 4}}{{\sqrt x + 2}} - 2\sqrt x } \right):\dfrac{1}{{\left( {\sqrt x - 2} \right)}}\) với \(x \ge 0,\,\,x \ne 4.\)
Bài 2 (1,5 điểm):
a) Vẽ Parabol \(\left( P \right):y = \dfrac{1}{2}{x^2}\) trên trục tọa độ \(Oxy\)
b) Tìm tham số \(m\) để đường thẳng \(\left( d \right):y = 2x + m\) cắt \(\left( P \right)\) tại hai điểm phân biệt.
Bài 3. (1,5 điểm)
a) (ID: 555544) Cho phương trình \(2{x^2} + 4x + m = 0\) (\(m\) là tham số). Tìm tất cả các giá trị của \(m\) để phương trình đã cho có hai nghiệm \({x_1},\,\,{x_2}\) thỏa mãn \(x_1^2 + x_2^2 = 10\).
b) (ID: 555545) Theo kế hoạch, công an tỉnh Kiên Giang điều 2 tổ công tác đến làm thẻ Căn cước công dân cho một phường trên địa bàn thành phố Rạch Giá. Nếu cả 2 tổ cùng làm thì trong 4 ngày hoàn thành công việc, Nếu mỗi tổ làm riêng thì thời gian hoàn thành của tổ I ít hơn thời gian hoàn thành của tố II là 6 ngày. Hỏi nếu làm riêng thì mỗi tổ phải làm trong bao nhiêu ngày để hoàn thành công việc?
Bài 4. (2,0 điểm)
Cho hai đường tròn \(\left( {O;R} \right)\) và \(\left( {O';r} \right)\) tiếp xúc ngoài tại \(A\,\,\left( {R > r} \right)\). Gọi \(BC\) là tiếp tuyến chung ngoài của hai đường tròn này (với \(B \in \left( O \right)\) và \(C \in \left( {O'} \right)\)). Tiếp tuyến chung tại \(A\) của hai đường tròn \(\left( O \right)\) và \(\left( {O'} \right)\) cắt đoạn thẳng \(BC\) tại \(M\).
a) Chứng minh \(OM\) vuông góc với \(O'M\).
b) Gọi \(E\) là giao điểm của \(AB\) với \(OM\) và \(F\) là giao điểm của \(AC\) với \(O'M\). Chứng minh tứ giác \(OEFO'\) nội tiếp một đường tròn.
c) Gọi \(I\) là tâm đường tròn ngoại tiếp tứ giác \(OEFO'\), \(K\) là trung điểm của đoạn \(AM\). Chứng minh \(OO' = 2IK\).
Bài 5 (1,5 điểm)
Các ăng ten parabol thu sóng hoạt động dựa theo nguyên lý: mọi tia sóng song song với trục của parabol đều có tia phản xạ đi qua tiêu điểm \(F\) của parabol (vì vậy nếu ta đặt thiết bị thu sóng tại \(F\) thì sẽ thu sóng được tốt nhất). Người ta chứng minh được rằng: Nếu đường thẳng vuông góc với trục của parabol tại \(F\) cắt parabol tại 2 điểm \(A,B\) thì \(OF = \dfrac{1}{4}AB\) với \(O\) là đỉnh của parabol (tham khảo hình vẽ).
Tính độ dài đoạn \(OF\)ứng với mô hình trên của một ăng ten parabol (ngang 90cm và cao 9 cm).
I. PHẦN TRẮC NGHIỆM
BẢNG ĐÁP ÁN
Câu | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
Đáp án | D | B | B | B | C | C | A | B | B | B | A | C | D | A | B |
Câu 1
Phương pháp:
Sử dụng hẳng đẳng thức \(\sqrt {{A^2}} = \left| A \right| = \left\{ \begin{array}{l}A\,\,\,khi\,\,\,A \ge 0\\ - A\,\,\,khi\,\,\,A < 0\end{array} \right.\)
Cách giải:
Ta có: \(\dfrac{{\sqrt {128} }}{{\sqrt 8 }} = \sqrt {\dfrac{{128}}{8}} = \sqrt {16} = \sqrt {{4^2}} = 4\)
Chọn D.
Câu 2 (NB)
Phương pháp:
Thay \(x = - 3\) vào hàm số để tính.
Cách giải:
Thay \(x = - 3\) vào \(y = \dfrac{1}{3}{x^2}\), ta được: \(y = \dfrac{1}{3}.{\left( { - 3} \right)^2} = \dfrac{1}{3}.9 = 3\)
Giá trị của hàm số \(y = \dfrac{1}{3}{x^2}\) tại điểm \(x = - 3\) là:\(3\)
Chọn B.
Câu 3 (NB)
Phương pháp:
Phương trình bậc hai \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\) có biệt thức là \(\Delta = {b^2} - 4ac\)
Cách giải:
Phương trình: \({x^2} - 3x - 1 = 0\) có \(a = 1;b = - 3;c = - 1\)
Khi đó, biệt thức \(\Delta = {\left( { - 3} \right)^2} - 4.1.\left( { - 1} \right) = 9 + 4 = 13\)
Chọn B.
Câu 4 (NB)
Phương pháp:
Phương trình bậc hai \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\) có \(a + b + c = 0\) thì phương trình có hai nghiệm phân biệt \({x_1} = 1;{x_2} = \dfrac{c}{a}\)
Cách giải:
Ta có: \(a + b + c = 1 + 2 + \left( { - 3} \right) = 0\), khi đó phương trình có hai nghiệm phân biệt \({x_1} = 1;{x_2} = - 3\)
Vậy phương trình có tập nghiệm là \(S = \left\{ {1; - 3} \right\}\)
Chọn B.
Câu 5 (NB)
Phương pháp:
Điểm \(M\left( {{x_0};{y_0}} \right)\) thuộc đồ thị \(y = ax + b\) khi \({y_0} = a{x_0} + b\)
Cách giải:
+ Thay \(x = 5\) vào \(y = 5x + 2\), ta được: \(y = 5.5 + 2 = 27 \ne 2\)
\( \Rightarrow M\left( {5;2} \right)\) không thuộc đồ thị hàm số \(y = 5x + 2\)
+ Thay \(x = 2\) vào \(y = 5x + 2\), ta được: \(y = 5.2 + 2 = 12 \ne 0\)
\( \Rightarrow P\left( {2;0} \right)\) không thuộc đồ thị hàm số \(y = 5x + 2\)
+ Thay \(x = 1\) vào \(y = 5x + 2\), ta được: \(y = 5.1 + 2 = 7\)
\( \Rightarrow N\left( {1;7} \right)\) thuộc đồ thị hàm số \(y = 5x + 2\)
Chọn C.
Câu 6 (NB)
Phương pháp:
Chu vi đường tròn có bán kính \(r\) được tính theo công thức \(C = 2\pi r\)
Cách giải:
Chu vi đường tròn có bán kính bằng \(3\) là: \(C = 2\pi .3 = 6\pi \)
Chọn C.
Câu 7 (NB)
Phương pháp:
Sử dụng phương pháp cộng đại số, tìm nghiệm của hệ phương trình.
Cách giải:
\(\left\{ \begin{array}{l}3x + y = 9\\2x + y = 7\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\2x + y = 7\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\2.2 + y = 7\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 3\end{array} \right.\)
Vậy hệ phương trình có nghiệm là \(\left( {x;y} \right) = \left( {2;3} \right)\)
Chọn A.
Câu 8 (NB)
Phương pháp:
Hàm số \(y = ax + b\) đồng biến trên \(\mathbb{R} \Leftrightarrow a > 0\)
Cách giải:
Hàm số \(y = x + 2\) có \(a = 1 > 0\) nên hàm số đồng biến trên \(\mathbb{R}\).
Chọn D.
Câu 9 (NB)
Phương pháp:
Hình nón có bán kính đáy \(r\), đường cao \(h\) thì thể tích của hình nón được tính theo công thức \(V = \dfrac{1}{3}\pi {r^2}h\)
Cách giải:
Thể tích của hình nón là \(V = \dfrac{1}{3}\pi {.3^2}.2 = 6\pi \left( {c{m^3}} \right)\)
Chọn B.
Câu 10 (NB)
Phương pháp:
Hai đường thẳng \(\left( {{d_1}} \right):y = {a_1}x + {b_1}\) và \(\left( {{d_2}} \right):y = {a_2}x + {b_2}\) song song với nhau \( \Leftrightarrow \left\{ \begin{array}{l}{a_1} = {a_2}\\{b_1} \ne {b_2}\end{array} \right.\)
Cách giải:
Hai đường thẳng \({d_1}:y = x + 2\) và \({d_2}:y = ax + 3\) song song với nhau khi \(\left\{ \begin{array}{l}a = 1\\3 \ne 2\end{array} \right. \Rightarrow a = 1\)
Chọn B.
Câu 11 (NB)
Phương pháp:
Biểu thức \(\sqrt {f\left( x \right)} \) có nghĩa \( \Leftrightarrow f\left( x \right) \ge 0\)
Cách giải:
Biểu thức \(\sqrt {2x - 2} \) có nghĩa khi \(2x - 2 \ge 0 \Leftrightarrow x \ge 1\)
Chọn A.
Câu 12 (TH)
Phương pháp:
Thay \(x = 2;x = - 3\) vào phương trình từ đó thu được hệ phương trình, giải hệ phương trình, tính \(b + c\)
Cách giải:
+ Với \(x = 2\), ta có: \({2^2} + 2b + c = 0 \Leftrightarrow 2b + c = - 4\,\,\,\left( 1 \right)\)
+ Với \(x = - 3\), ta có: \({\left( { - 3} \right)^2} + \left( { - 3} \right).b + c = 0 \Leftrightarrow 3b - c = 9\,\,\,\,\left( 2 \right)\)
Từ (1) và (2), ta có hệ phương trình \(\left\{ \begin{array}{l}2b + c = - 4\\3b - c = 9\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}5b = 5\\c = 3b - 9\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = 1\\c = - 6\end{array} \right.\)
Do đó, \(a + b = - 5\)
Chọn C.
Câu 13 (TH)
Phương pháp:
Áp dụng hệ thức lượng trong tam giác vuông.
Cách giải:
\(\Delta ABC\) vuông tại \(A,\) đường cao \(AH\), áp dụng hệ thức lượng trong tam giác vuông, ta có:
\(\begin{array}{l}\,\,\,\,\,\,\,\,A{H^2} = BH.CH\\ \Leftrightarrow A{H^2} = 2.3\\ \Leftrightarrow A{H^2} = 6\\ \Rightarrow AH = \sqrt 6 \left( {cm} \right)\end{array}\)
Vậy \(AH = \sqrt 6 cm\)
Chọn D.
Câu 14 (TH)
Phương pháp:
Hình trụ có bán kính đáy \(r\), chiều cao \(h\) thì diện tích xung quanh tính theo công thức \(2\pi rh\).
Cách giải:
Bán kính đáy của hình trụ là: \(r = 8:2 = 4\left( {cm} \right)\)
Diện tích xung quanh của hình trụ là: \({S_{xq}} = 2\pi rh = 2\pi .4.12 = 96\pi \left( {c{m^2}} \right)\)
Chọn A.
Câu 15 (TH)
Phương pháp:
Diện tích của mặt cầu có bán kính \(R\) được tính theo công thức: \(S = 4\pi {R^2}\)
Cách giải:
Bán kính của mặt cầu là: \(R = \dfrac{d}{2}\)
Diện tích của mặt cầu là: \(S = 4\pi {R^2} = 4\pi .{\left( {\dfrac{d}{2}} \right)^2} = \pi {d^2}\)
Chọn B.
II. TỰ LUẬN
Bài 1 (TH)
Phương pháp:
a) Sử dụng hẳng đẳng thức: \(\sqrt {{A^2}} = \left| A \right| = \left\{ \begin{array}{l}A\,\,\,khi\,\,A \ge 0\\ - A\,\,\,khi\,\,\,A < 0\end{array} \right.\)
Thực hiện phép toán với các căn bậc hai
b) Rút gọn các phân thức, thực hiện các phép toán để rút gọn biểu thức.
Cách giải:
a) Thực hiện phép tính \(A = \sqrt {112} - \sqrt {63} \)
\(A = \sqrt {112} - \sqrt {63} = \sqrt {16.7} - \sqrt {9.7} = 4\sqrt 7 - 3\sqrt 7 = \sqrt 7 \)
Vậy \(A = \sqrt 7 \).
b) Rút gọn biểu thức \(B = \left( {\dfrac{{x - 4}}{{\sqrt x + 2}} - 2\sqrt x } \right):\dfrac{1}{{\left( {\sqrt x - 2} \right)}}\) với \(x \ge 0,\,\,x \ne 4.\)
Với \(x \ge 0,\,\,x \ne 4\) ta có:
\(B = \left( {\dfrac{{x - 4}}{{\sqrt x + 2}} - 2\sqrt x } \right):\dfrac{1}{{\left( {\sqrt x - 2} \right)}}\)
\( = \left( {\dfrac{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}}{{\sqrt x + 2}} - 2\sqrt x } \right).\left( {\sqrt x - 2} \right)\)
\(\begin{array}{l} = \left( {\sqrt x - 2 - 2\sqrt x } \right).\left( {\sqrt x - 2} \right)\\ = \left( { - \sqrt x - 2} \right).\left( {\sqrt x - 2} \right)\\ = - \left( {\sqrt x + 2} \right).\left( {\sqrt x - 2} \right)\\ = - \left( {x - 4} \right)\\ = - x + 4\end{array}\)
Vậy \(B = - x + 4\) với \(x \ge 0,\,\,x \ne 4.\)
Câu 2 (VD)
Phương pháp:
a) Vẽ đồ thị của hàm số \(y = a{x^2}\left( {a \ne 0} \right)\)
+ Nhận xét về hệ số \(a\) và sự biến thiên của hàm số
+ Lập bảng giá trị tương ứng của \(x\) và \(y\)
+ Xác định được các điểm mà đồ thị đi qua, vẽ đồ thị.
b) Xét phương trình hoành độ giao điểm của đường thẳng \(\left( d \right)\) và Parabol \(\left( P \right)\) là phương trình (*)
Đường thẳng \(\left( d \right)\) cắt \(\left( P \right)\) tại hai điểm phân biệt \( \Leftrightarrow \left( * \right)\) có hai nghiệm phân biệt \( \Leftrightarrow \Delta ' > 0\)
Cách giải:
a) Vẽ Parabol \(\left( P \right):y = \dfrac{1}{2}{x^2}\) trên trục tọa độ \(Oxy\)
Ta có: \(a = \dfrac{1}{2} > 0\) nên đồ thị có bề lõm hướng lên trên, đồ thị hàm số đi qua gốc tọa độ \(O\left( {0;0} \right)\) và nhận trục \(Oy\) làm trục đối xứng.
Hàm số đồng biến khi \(x > 0\) và nghịch biến khi \(x < 0\).
Bảng giá trị:
\(x\) | \( - 2\) | \( - 1\) | \(0\) | \(1\) | \(2\) |
\(y = \dfrac{1}{2}{x^2}\) | \(2\) | \(\dfrac{1}{2}\) | \(0\) | \(\dfrac{1}{2}\) | \(2\) |
\( \Rightarrow \left( P \right):\,\,y = \dfrac{1}{2}{x^2}\) là đường cong đi qua các điểm \(\left( { - 2;2} \right);\,\,\left( { - 1;\dfrac{1}{2}} \right);\,\,\left( {0;0} \right);\,\,\left( {1;\dfrac{1}{2}} \right);\,\,\left( {2;2} \right)\).
Đồ thị hàm số:
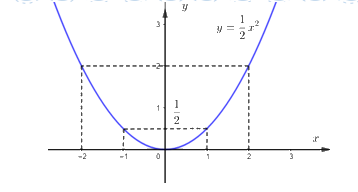
b) Tìm tham số \(m\) để đường thẳng \(\left( d \right):y = 2x + m\) cắt \(\left( P \right)\) tại hai điểm phân biệt.
Hoành độ giao điểm của đường thẳng \(\left( d \right)\) và Parabol \(\left( P \right)\) là nghiệm của phương trình:
\(\begin{array}{l}\,\,\,\,\,\,\,\dfrac{1}{2}{x^2} = 2x + m\\ \Leftrightarrow {x^2} = 4x + 2m\\ \Leftrightarrow {x^2} - 4x - 2m = 0\,\,\,\,\,\left( * \right)\end{array}\)
Ta có: \(\Delta ' = {\left( { - 2} \right)^2} - 1.\left( { - 2m} \right) = 4 + 2m\).
Đường thẳng \(\left( d \right):y = 2x + m\) cắt \(\left( P \right)\) tại hai điểm phân biệt
\( \Leftrightarrow \left( * \right)\) có hai nghiệm phân biệt
\(\begin{array}{l} \Leftrightarrow \Delta ' > 0\\ \Leftrightarrow 2m + 4 > 0\\ \Leftrightarrow m > - 2\end{array}\)
Vậy \(m > - 2\) thì đường thẳng \(\left( d \right):y = 2x + m\) cắt \(\left( P \right)\) tại hai điểm phân biệt.
Bài 3 (VD)
Phương pháp:
Phương trình \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\) có nghiệm \( \Leftrightarrow \Delta ' \ge 0\)
Áp dụng hệ thức Vi – ét, ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = \dfrac{{ - b}}{a}\\{x_1}{x_2} = \dfrac{c}{a}\end{array} \right.\)
Biến đổi vế phải của phương trình: \(x_1^2 + x_2^2 = {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2}\), sau đó giải phương trình tìm \(m\)
b) Gọi thời gian làm riêng hoàn thành công việc của tổ I, tổ II lần lượt là \(x,\,\,y\) ngày (ĐK: \(x,\,\,y \in {\mathbb{N}^*}\)).
Tính được số phân công việc mà mỗi ngày mỗi tổ làm việc.
Lập hệ phương trình, giải hệ phương trình, đối chiếu điều kiện và kết luận.
Cách giải:
a) Cho phương trình \(2{x^2} + 4x + m = 0\) (\(m\) là tham số). Tìm tất cả các giá trị của \(m\) để phương trình đã cho có hai nghiệm \({x_1},\,\,{x_2}\) thỏa mãn \(x_1^2 + x_2^2 = 10\).
Ta có \(\Delta ' = {2^2} - 2m = 4 - 2m\).
Để phương trình đã cho có 2 nghiệm \({x_1},\,\,{x_2}\) thì \(\Delta ' \ge 0 \Leftrightarrow 4 - 2m \ge 0 \Leftrightarrow m \le 2\).
Khi đó áp dụng định lí Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = - 2\\{x_1}{x_2} = \dfrac{m}{2}\end{array} \right.\).
Ta có:
Vậy \(m = - 6\).
b) Theo kế hoạch, công an tỉnh Kiên Giang điều 2 tổ công tác đến làm thẻ Căn cước công dân cho một phường trên địa bàn thành phố Rạch Giá. Nếu cả 2 tổ cùng làm thì trong 4 ngày hoàn thành công việc, Nếu mỗi tổ làm riêng thì thời gian hoàn thành của tổ I ít hơn thời gian hoàn thành của tố II là 6 ngày. Hỏi nếu làm riêng thì mỗi tổ phải làm trong bao nhiêu ngày để hoàn thành công việc?
Gọi thời gian làm riêng hoàn thành công việc của tổ I, tổ II lần lượt là \(x,\,\,y\) ngày (ĐK: \(x,\,\,y \in {\mathbb{N}^*}\)).
\( \Rightarrow \) Mỗi ngày tổ I làm được \(\dfrac{1}{x}\) phần công việc, mỗi ngày tổ II làm được \(\dfrac{1}{y}\) phần công việc.
Vì nếu cả 2 tổ cùng làm thì trong 4 ngày hoàn thành công việc nên ta có phương trình \(\dfrac{1}{x} + \dfrac{1}{y} = \dfrac{1}{4}\,\,\left( 1 \right)\).
Vì nếu mỗi tổ làm riêng thì thời gian hoàn thành của tổ I ít hơn thời gian hoàn thành của tố II là 6 ngày nên ta có phương trình \(x + 6 = y\,\,\left( 2 \right)\).
Từ (1) và (2) ta có hệ phương trình: \(\left\{ \begin{array}{l}\dfrac{1}{x} + \dfrac{1}{y} = \dfrac{1}{4}\\x + 6 = y\end{array} \right.\)
\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}\dfrac{1}{x} + \dfrac{1}{{x + 6}} = \dfrac{1}{4}\\x + 6 = y\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\dfrac{{x + 6 + x}}{{x\left( {x + 6} \right)}} = \dfrac{1}{4}\\x + 6 = y\end{array} \right. \Rightarrow \left\{ \begin{array}{l}\dfrac{{2x + 6}}{{x\left( {x + 6} \right)}} = \dfrac{1}{4}\\x + 6 = y\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}8x + 24 = {x^2} + 6x\\x + 6 = y\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x^2} - 2x - 24 = 0\,\,\left( * \right)\\x + 6 = y\end{array} \right.\end{array}\)
Phương trình (*) có \(\Delta ' = {1^2} + 24 = 25 = {5^2} > 0\) nên phương trình (*) có 2 nghiệm phân biệt \(\left[ \begin{array}{l}x = 1 + 5 = 6\,\,\left( {tm} \right)\\x = 1 - 5 = - 4\,\,\left( {ktm} \right)\end{array} \right.\)
Với \(x = 6 \Rightarrow y = x + 6 = 6 + 6 = 12\,\,\left( {tm} \right)\).
Vậy thời gian làm riêng hoàn thành công việc của tổ I, tổ II lần lượt là \(6\) ngày và \(12\) ngày.
Bài 4 (VD)
Phương pháp:
a) Sử dụng tính chất hai tiếp tuyến cắt nhau của đường tròn.
b) Vận dụng dấu hiệu: Tứ giác có góc ngoài bằng góc trong tại đỉnh đối diện là tứ giác nội tiếp.
c) Gọi \(N\) là trung điểm của \(OO'\).
Ta sẽ chứng minh: \(MN//IK\),\(MK//IN\)\( \Rightarrow MNIK\) là hình bình hành (dhnb) \( \Rightarrow MN = IK\) (tính chất hình bình hành).
Mà \(OO' = 2MN\)
Vậy \(OO' = 2IK\,\,\left( {dpcm} \right)\)
Cách giải:
Cho hai đường tròn \(\left( {O;R} \right)\) và \(\left( {O';r} \right)\) tiếp xúc ngoài tại \(A\,\,\left( {R > r} \right)\). Gọi \(BC\) là tiếp tuyến chung ngoài của hai đường tròn này (với \(B \in \left( O \right)\) và \(C \in \left( {O'} \right)\)). Tiếp tuyến chung tại \(A\) của hai đường tròn \(\left( O \right)\) và \(\left( {O'} \right)\) cắt đoạn thẳng \(BC\) tại \(M\).
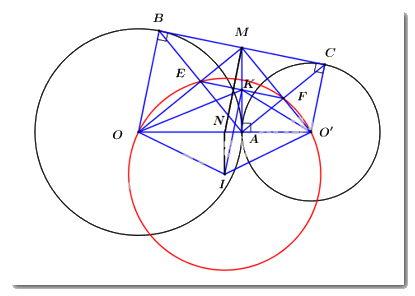
a) Chứng minh \(OM\) vuông góc với \(O'M\).
Theo tính chất 2 tiếp tuyến cắt nhau tại có:
\(MO\) là tia phân giác của \(\angle AMB\) \( \Rightarrow \angle OMA = \dfrac{1}{2}\angle AMB\).
\(MO'\) là tia phân giác của \(\angle AMC\) \( \Rightarrow \angle O'MA = \dfrac{1}{2}\angle AMC\).
\( \Rightarrow \angle OMO' = \angle OAM + \angle O'MA = \dfrac{1}{2}\left( {AMB + \angle AMC} \right) = \dfrac{1}{2}{.180^0} = {90^0}\).
Vậy \(OM \bot O'M\).
b) Gọi \(E\) là giao điểm của \(AB\) với \(OM\) và \(F\) là giao điểm của \(AC\) với \(O'M\). Chứng minh tứ giác \(OEFO'\) nội tiếp một đường tròn.
Ta có: \(MA = MB\) (tính chất 2 tiếp tuyến cắt nhau) \( \Rightarrow M\) thuộc trung trực của \(AB\).
\(OA = OB\,\,\left( { = R} \right)\) \( \Rightarrow O\) thuộc trung trực của \(AB\).
\( \Rightarrow OM\) là trung trực của \(AB\)
\( \Rightarrow OM \bot AB\) tại \(E\).
Chứng minh hoàn toàn tương tự ta có \(O'M \bot AC\) tại \(F\).
Xét tứ giác \(AEMF\) có: \(\angle AEM = \angle AFM = \angle EMF = {90^0}\) \( \Rightarrow AEMF\) là hình chữ nhật (dhnb).
\( \Rightarrow AEMF\) là tứ giác nội tiếp.
\( \Rightarrow \angle MFE = \angle MAE\) (2 góc nội tiếp cùng chắn cung \(ME\)).
Mà \(\angle MAE = \angle MOA\) (cùng phụ với \(\angle OAE\)) \( \Rightarrow \angle MFE = \angle MOA\).
\( \Rightarrow OEFO'\) là tứ giác nội tiếp (tứ giác có góc ngoài bằng góc trong tại đỉnh đối diện).
c) Gọi \(I\) là tâm đường tròn ngoại tiếp tứ giác \(OEFO'\), \(K\) là trung điểm của đoạn \(AM\). Chứng minh \(OO' = 2IK\).
Gọi \(N\) là trung điểm của \(OO'\).
Vì \(\Delta OMO'\) vuông tại \(M\,\,\left( {\angle OMO = {{90}^0}} \right)\,\,\left( {cmt} \right)\) nên \(MN = \dfrac{1}{2}OO' \Rightarrow OO' = 2MN\) (trung tuyến ứng với cạnh huyền trong tam giác vuông bằng nửa cạnh huyền).
Vì \(OM,\,\,O'M\) lần lượt là trung trực của \(AB,\,\,AC\) nên \(E,\,\,F\) lần lượt là trung điểm của \(AB,\,\,AC\).
\( \Rightarrow EF\) là đường trung bình của \(\Delta ABC\) (định nghĩa)
\( \Rightarrow EF = \dfrac{1}{2}BC\) (tính chất đường trung bình của tam giác).
Lại có \(MN\) là đường trung bình của hình thang \(OBCO'\) nên \(MN//OB//O'C\) \( \Rightarrow MN \bot BC\,\,\left( {do\,\,OB \bot BC} \right)\)
Mà \(EF//BC\,\,\left( {cmt} \right) \Rightarrow MN \bot EF\) (từ vuông góc đến song song).
Vì \(K\) là trung điểm của \(AM\), mà \(AEMF\) là hình chữ nhật (cmt) \( \Rightarrow K\) cũng là trung điểm của \(EF\).
\( \Rightarrow IK \bot EF\) (quan hệ vuông góc giữa đường kính và dây cung).
\( \Rightarrow MN//IK\) (từ vuông góc đến song song). (1)
Ta có: \(\left\{ \begin{array}{l}MK \bot OO'\,\,\left( {do\,\,MA \bot OO'} \right)\\IN \bot OO'\end{array} \right. \Rightarrow MK//IN\) (2)
Từ (1) và (2) \( \Rightarrow MNIK\) là hình bình hành (dhnb) \( \Rightarrow MN = IK\) (tính chất hình bình hành).
Mà \(OO' = 2MN\,\,\left( {cmt} \right)\)
Vậy \(OO' = 2IK\,\,\left( {dpcm} \right)\)
Bài 5 (VDC)
Phương pháp:
Ta gắn trục tọa độ của parabol và các điểm M, N vào hệ trục tọa độ \(Oxy\) với \(Oy\) là tia \(OF\) và \(Ox\) là tia thuộc đường thẳng vuông góc với \(OF\) tại \(O\) để giải bài toán.
Cách giải:
Các ăng ten parabol thu sóng hoạt động dựa theo nguyên lý: mọi tia sóng song song với trục của parabol đều có tia phản xạ đi qua tiêu điểm \(F\) của parabol (vì vậy nếu ta đặt thiết bị thu sóng tại \(F\) thì sẽ thu sóng được tốt nhất). Người ta chứng minh được rằng: Nếu đường thẳng vuông góc với trục của parabol tại \(F\) cắt parabol tại 2 điểm \(A,B\) thì \(OF = \dfrac{1}{4}AB\) với \(O\) là đỉnh của parabol (tham khảo hình vẽ).

Tính độ dài đoạn \(OF\)ứng với mô hình trên của một ăng ten parabol (ngang 90cm và cao 9 cm).
Ta gắn trục tọa độ của parabol và các điểm M, N vào hệ trục tọa độ \(Oxy\) với \(Oy\) là tia \(OF\) và \(Ox\) là tia thuộc đường thẳng vuông góc với \(OF\) tại \(O\), khi đó parabol đi qua gốc tọa độ và có dạng \(y = a{x^2}\) và hoành độ của điểm N bằng \(\dfrac{{MN}}{2}\) hay \(N\) có tọa độ là \(N\left( {45;9} \right)\),
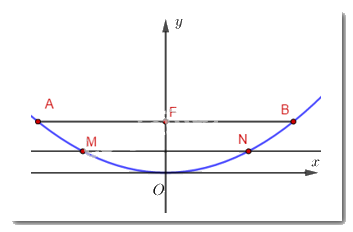
Parabol đi qua hai điểm \(M,N\) nên ta có: \(9 = a{.45^2} \Leftrightarrow a = \dfrac{1}{{225}}\)
\( \Rightarrow \) Parabol là: \(y = \dfrac{1}{{225}}{x^2}\).
Đường thẳng vuông góc với trục của parabol tại \(F\) cắt parabol tại 2 điểm \(A,\,\,B\) nên hai điểm A và B thuộc parabol.
Gọi tọa độ của \(F\) là \(F\left( {0;t} \right)\,\,\left( {t > 0} \right)\), tọa độ của \(B\) là \(B\left( {{x_B},{y_B}} \right)\).
\(OF = \dfrac{1}{4}AB \Rightarrow FB = \dfrac{1}{2}AB = \dfrac{1}{2}.4OF = 2OF = 2t\)\( \Rightarrow {x_B} = FB = 2t\)
\(F,A,B\) cùng thuộc đường thẳng \(AB\) và song song với trục hoành nên có tung độ bằng nhau.
\( \Rightarrow {y_B} = t \Rightarrow B\left( {2t;t} \right)\).
Vì \(B\) là điểm thuộc parabol \(y = \dfrac{1}{{225}}{x^2}\) nên
\(t = \dfrac{1}{{225}}.{\left( {2t} \right)^2} \Leftrightarrow 4{t^2} = 225t \Leftrightarrow 4{t^2} - 225t = 0 \Leftrightarrow t\left( {4t - 225} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}t = 0\,\,\,\,\,\left( {ktm} \right)\\t = \dfrac{{225}}{4}\,\,\left( {tm} \right)\end{array} \right.\)
\( \Rightarrow OF = t = \dfrac{{225}}{4} = 56,25\left( {cm} \right)\)
Vậy \(OF = 56,25cm\).
I. PHẦN TRẮC NGHIỆM
BẢNG ĐÁP ÁN
Câu | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
Đáp án | D | B | B | B | C | C | A | B | B | B | A | C | D | A | B |
Câu 1
Phương pháp:
Sử dụng hẳng đẳng thức \(\sqrt {{A^2}} = \left| A \right| = \left\{ \begin{array}{l}A\,\,\,khi\,\,\,A \ge 0\\ - A\,\,\,khi\,\,\,A < 0\end{array} \right.\)
Cách giải:
Ta có: \(\dfrac{{\sqrt {128} }}{{\sqrt 8 }} = \sqrt {\dfrac{{128}}{8}} = \sqrt {16} = \sqrt {{4^2}} = 4\)
Chọn D.
Câu 2 (NB)
Phương pháp:
Thay \(x = - 3\) vào hàm số để tính.
Cách giải:
Thay \(x = - 3\) vào \(y = \dfrac{1}{3}{x^2}\), ta được: \(y = \dfrac{1}{3}.{\left( { - 3} \right)^2} = \dfrac{1}{3}.9 = 3\)
Giá trị của hàm số \(y = \dfrac{1}{3}{x^2}\) tại điểm \(x = - 3\) là:\(3\)
Chọn B.
Câu 3 (NB)
Phương pháp:
Phương trình bậc hai \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\) có biệt thức là \(\Delta = {b^2} - 4ac\)
Cách giải:
Phương trình: \({x^2} - 3x - 1 = 0\) có \(a = 1;b = - 3;c = - 1\)
Khi đó, biệt thức \(\Delta = {\left( { - 3} \right)^2} - 4.1.\left( { - 1} \right) = 9 + 4 = 13\)
Chọn B.
Câu 4 (NB)
Phương pháp:
Phương trình bậc hai \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\) có \(a + b + c = 0\) thì phương trình có hai nghiệm phân biệt \({x_1} = 1;{x_2} = \dfrac{c}{a}\)
Cách giải:
Ta có: \(a + b + c = 1 + 2 + \left( { - 3} \right) = 0\), khi đó phương trình có hai nghiệm phân biệt \({x_1} = 1;{x_2} = - 3\)
Vậy phương trình có tập nghiệm là \(S = \left\{ {1; - 3} \right\}\)
Chọn B.
Câu 5 (NB)
Phương pháp:
Điểm \(M\left( {{x_0};{y_0}} \right)\) thuộc đồ thị \(y = ax + b\) khi \({y_0} = a{x_0} + b\)
Cách giải:
+ Thay \(x = 5\) vào \(y = 5x + 2\), ta được: \(y = 5.5 + 2 = 27 \ne 2\)
\( \Rightarrow M\left( {5;2} \right)\) không thuộc đồ thị hàm số \(y = 5x + 2\)
+ Thay \(x = 2\) vào \(y = 5x + 2\), ta được: \(y = 5.2 + 2 = 12 \ne 0\)
\( \Rightarrow P\left( {2;0} \right)\) không thuộc đồ thị hàm số \(y = 5x + 2\)
+ Thay \(x = 1\) vào \(y = 5x + 2\), ta được: \(y = 5.1 + 2 = 7\)
\( \Rightarrow N\left( {1;7} \right)\) thuộc đồ thị hàm số \(y = 5x + 2\)
Chọn C.
Câu 6 (NB)
Phương pháp:
Chu vi đường tròn có bán kính \(r\) được tính theo công thức \(C = 2\pi r\)
Cách giải:
Chu vi đường tròn có bán kính bằng \(3\) là: \(C = 2\pi .3 = 6\pi \)
Chọn C.
Câu 7 (NB)
Phương pháp:
Sử dụng phương pháp cộng đại số, tìm nghiệm của hệ phương trình.
Cách giải:
\(\left\{ \begin{array}{l}3x + y = 9\\2x + y = 7\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\2x + y = 7\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\2.2 + y = 7\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 3\end{array} \right.\)
Vậy hệ phương trình có nghiệm là \(\left( {x;y} \right) = \left( {2;3} \right)\)
Chọn A.
Câu 8 (NB)
Phương pháp:
Hàm số \(y = ax + b\) đồng biến trên \(\mathbb{R} \Leftrightarrow a > 0\)
Cách giải:
Hàm số \(y = x + 2\) có \(a = 1 > 0\) nên hàm số đồng biến trên \(\mathbb{R}\).
Chọn D.
Câu 9 (NB)
Phương pháp:
Hình nón có bán kính đáy \(r\), đường cao \(h\) thì thể tích của hình nón được tính theo công thức \(V = \dfrac{1}{3}\pi {r^2}h\)
Cách giải:
Thể tích của hình nón là \(V = \dfrac{1}{3}\pi {.3^2}.2 = 6\pi \left( {c{m^3}} \right)\)
Chọn B.
Câu 10 (NB)
Phương pháp:
Hai đường thẳng \(\left( {{d_1}} \right):y = {a_1}x + {b_1}\) và \(\left( {{d_2}} \right):y = {a_2}x + {b_2}\) song song với nhau \( \Leftrightarrow \left\{ \begin{array}{l}{a_1} = {a_2}\\{b_1} \ne {b_2}\end{array} \right.\)
Cách giải:
Hai đường thẳng \({d_1}:y = x + 2\) và \({d_2}:y = ax + 3\) song song với nhau khi \(\left\{ \begin{array}{l}a = 1\\3 \ne 2\end{array} \right. \Rightarrow a = 1\)
Chọn B.
Câu 11 (NB)
Phương pháp:
Biểu thức \(\sqrt {f\left( x \right)} \) có nghĩa \( \Leftrightarrow f\left( x \right) \ge 0\)
Cách giải:
Biểu thức \(\sqrt {2x - 2} \) có nghĩa khi \(2x - 2 \ge 0 \Leftrightarrow x \ge 1\)
Chọn A.
Câu 12 (TH)
Phương pháp:
Thay \(x = 2;x = - 3\) vào phương trình từ đó thu được hệ phương trình, giải hệ phương trình, tính \(b + c\)
Cách giải:
+ Với \(x = 2\), ta có: \({2^2} + 2b + c = 0 \Leftrightarrow 2b + c = - 4\,\,\,\left( 1 \right)\)
+ Với \(x = - 3\), ta có: \({\left( { - 3} \right)^2} + \left( { - 3} \right).b + c = 0 \Leftrightarrow 3b - c = 9\,\,\,\,\left( 2 \right)\)
Từ (1) và (2), ta có hệ phương trình \(\left\{ \begin{array}{l}2b + c = - 4\\3b - c = 9\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}5b = 5\\c = 3b - 9\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = 1\\c = - 6\end{array} \right.\)
Do đó, \(a + b = - 5\)
Chọn C.
Câu 13 (TH)
Phương pháp:
Áp dụng hệ thức lượng trong tam giác vuông.
Cách giải:
\(\Delta ABC\) vuông tại \(A,\) đường cao \(AH\), áp dụng hệ thức lượng trong tam giác vuông, ta có:
\(\begin{array}{l}\,\,\,\,\,\,\,\,A{H^2} = BH.CH\\ \Leftrightarrow A{H^2} = 2.3\\ \Leftrightarrow A{H^2} = 6\\ \Rightarrow AH = \sqrt 6 \left( {cm} \right)\end{array}\)
Vậy \(AH = \sqrt 6 cm\)
Chọn D.
Câu 14 (TH)
Phương pháp:
Hình trụ có bán kính đáy \(r\), chiều cao \(h\) thì diện tích xung quanh tính theo công thức \(2\pi rh\).
Cách giải:
Bán kính đáy của hình trụ là: \(r = 8:2 = 4\left( {cm} \right)\)
Diện tích xung quanh của hình trụ là: \({S_{xq}} = 2\pi rh = 2\pi .4.12 = 96\pi \left( {c{m^2}} \right)\)
Chọn A.
Câu 15 (TH)
Phương pháp:
Diện tích của mặt cầu có bán kính \(R\) được tính theo công thức: \(S = 4\pi {R^2}\)
Cách giải:
Bán kính của mặt cầu là: \(R = \dfrac{d}{2}\)
Diện tích của mặt cầu là: \(S = 4\pi {R^2} = 4\pi .{\left( {\dfrac{d}{2}} \right)^2} = \pi {d^2}\)
Chọn B.
II. TỰ LUẬN
Bài 1 (TH)
Phương pháp:
a) Sử dụng hẳng đẳng thức: \(\sqrt {{A^2}} = \left| A \right| = \left\{ \begin{array}{l}A\,\,\,khi\,\,A \ge 0\\ - A\,\,\,khi\,\,\,A < 0\end{array} \right.\)
Thực hiện phép toán với các căn bậc hai
b) Rút gọn các phân thức, thực hiện các phép toán để rút gọn biểu thức.
Cách giải:
a) Thực hiện phép tính \(A = \sqrt {112} - \sqrt {63} \)
\(A = \sqrt {112} - \sqrt {63} = \sqrt {16.7} - \sqrt {9.7} = 4\sqrt 7 - 3\sqrt 7 = \sqrt 7 \)
Vậy \(A = \sqrt 7 \).
b) Rút gọn biểu thức \(B = \left( {\dfrac{{x - 4}}{{\sqrt x + 2}} - 2\sqrt x } \right):\dfrac{1}{{\left( {\sqrt x - 2} \right)}}\) với \(x \ge 0,\,\,x \ne 4.\)
Với \(x \ge 0,\,\,x \ne 4\) ta có:
\(B = \left( {\dfrac{{x - 4}}{{\sqrt x + 2}} - 2\sqrt x } \right):\dfrac{1}{{\left( {\sqrt x - 2} \right)}}\)
\( = \left( {\dfrac{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}}{{\sqrt x + 2}} - 2\sqrt x } \right).\left( {\sqrt x - 2} \right)\)
\(\begin{array}{l} = \left( {\sqrt x - 2 - 2\sqrt x } \right).\left( {\sqrt x - 2} \right)\\ = \left( { - \sqrt x - 2} \right).\left( {\sqrt x - 2} \right)\\ = - \left( {\sqrt x + 2} \right).\left( {\sqrt x - 2} \right)\\ = - \left( {x - 4} \right)\\ = - x + 4\end{array}\)
Vậy \(B = - x + 4\) với \(x \ge 0,\,\,x \ne 4.\)
Câu 2 (VD)
Phương pháp:
a) Vẽ đồ thị của hàm số \(y = a{x^2}\left( {a \ne 0} \right)\)
+ Nhận xét về hệ số \(a\) và sự biến thiên của hàm số
+ Lập bảng giá trị tương ứng của \(x\) và \(y\)
+ Xác định được các điểm mà đồ thị đi qua, vẽ đồ thị.
b) Xét phương trình hoành độ giao điểm của đường thẳng \(\left( d \right)\) và Parabol \(\left( P \right)\) là phương trình (*)
Đường thẳng \(\left( d \right)\) cắt \(\left( P \right)\) tại hai điểm phân biệt \( \Leftrightarrow \left( * \right)\) có hai nghiệm phân biệt \( \Leftrightarrow \Delta ' > 0\)
Cách giải:
a) Vẽ Parabol \(\left( P \right):y = \dfrac{1}{2}{x^2}\) trên trục tọa độ \(Oxy\)
Ta có: \(a = \dfrac{1}{2} > 0\) nên đồ thị có bề lõm hướng lên trên, đồ thị hàm số đi qua gốc tọa độ \(O\left( {0;0} \right)\) và nhận trục \(Oy\) làm trục đối xứng.
Hàm số đồng biến khi \(x > 0\) và nghịch biến khi \(x < 0\).
Bảng giá trị:
\(x\) | \( - 2\) | \( - 1\) | \(0\) | \(1\) | \(2\) |
\(y = \dfrac{1}{2}{x^2}\) | \(2\) | \(\dfrac{1}{2}\) | \(0\) | \(\dfrac{1}{2}\) | \(2\) |
\( \Rightarrow \left( P \right):\,\,y = \dfrac{1}{2}{x^2}\) là đường cong đi qua các điểm \(\left( { - 2;2} \right);\,\,\left( { - 1;\dfrac{1}{2}} \right);\,\,\left( {0;0} \right);\,\,\left( {1;\dfrac{1}{2}} \right);\,\,\left( {2;2} \right)\).
Đồ thị hàm số:
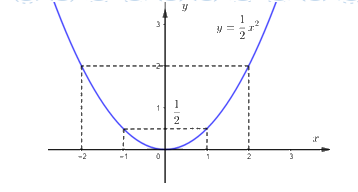
b) Tìm tham số \(m\) để đường thẳng \(\left( d \right):y = 2x + m\) cắt \(\left( P \right)\) tại hai điểm phân biệt.
Hoành độ giao điểm của đường thẳng \(\left( d \right)\) và Parabol \(\left( P \right)\) là nghiệm của phương trình:
\(\begin{array}{l}\,\,\,\,\,\,\,\dfrac{1}{2}{x^2} = 2x + m\\ \Leftrightarrow {x^2} = 4x + 2m\\ \Leftrightarrow {x^2} - 4x - 2m = 0\,\,\,\,\,\left( * \right)\end{array}\)
Ta có: \(\Delta ' = {\left( { - 2} \right)^2} - 1.\left( { - 2m} \right) = 4 + 2m\).
Đường thẳng \(\left( d \right):y = 2x + m\) cắt \(\left( P \right)\) tại hai điểm phân biệt
\( \Leftrightarrow \left( * \right)\) có hai nghiệm phân biệt
\(\begin{array}{l} \Leftrightarrow \Delta ' > 0\\ \Leftrightarrow 2m + 4 > 0\\ \Leftrightarrow m > - 2\end{array}\)
Vậy \(m > - 2\) thì đường thẳng \(\left( d \right):y = 2x + m\) cắt \(\left( P \right)\) tại hai điểm phân biệt.
Bài 3 (VD)
Phương pháp:
Phương trình \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\) có nghiệm \( \Leftrightarrow \Delta ' \ge 0\)
Áp dụng hệ thức Vi – ét, ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = \dfrac{{ - b}}{a}\\{x_1}{x_2} = \dfrac{c}{a}\end{array} \right.\)
Biến đổi vế phải của phương trình: \(x_1^2 + x_2^2 = {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2}\), sau đó giải phương trình tìm \(m\)
b) Gọi thời gian làm riêng hoàn thành công việc của tổ I, tổ II lần lượt là \(x,\,\,y\) ngày (ĐK: \(x,\,\,y \in {\mathbb{N}^*}\)).
Tính được số phân công việc mà mỗi ngày mỗi tổ làm việc.
Lập hệ phương trình, giải hệ phương trình, đối chiếu điều kiện và kết luận.
Cách giải:
a) Cho phương trình \(2{x^2} + 4x + m = 0\) (\(m\) là tham số). Tìm tất cả các giá trị của \(m\) để phương trình đã cho có hai nghiệm \({x_1},\,\,{x_2}\) thỏa mãn \(x_1^2 + x_2^2 = 10\).
Ta có \(\Delta ' = {2^2} - 2m = 4 - 2m\).
Để phương trình đã cho có 2 nghiệm \({x_1},\,\,{x_2}\) thì \(\Delta ' \ge 0 \Leftrightarrow 4 - 2m \ge 0 \Leftrightarrow m \le 2\).
Khi đó áp dụng định lí Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = - 2\\{x_1}{x_2} = \dfrac{m}{2}\end{array} \right.\).
Ta có:
Vậy \(m = - 6\).
b) Theo kế hoạch, công an tỉnh Kiên Giang điều 2 tổ công tác đến làm thẻ Căn cước công dân cho một phường trên địa bàn thành phố Rạch Giá. Nếu cả 2 tổ cùng làm thì trong 4 ngày hoàn thành công việc, Nếu mỗi tổ làm riêng thì thời gian hoàn thành của tổ I ít hơn thời gian hoàn thành của tố II là 6 ngày. Hỏi nếu làm riêng thì mỗi tổ phải làm trong bao nhiêu ngày để hoàn thành công việc?
Gọi thời gian làm riêng hoàn thành công việc của tổ I, tổ II lần lượt là \(x,\,\,y\) ngày (ĐK: \(x,\,\,y \in {\mathbb{N}^*}\)).
\( \Rightarrow \) Mỗi ngày tổ I làm được \(\dfrac{1}{x}\) phần công việc, mỗi ngày tổ II làm được \(\dfrac{1}{y}\) phần công việc.
Vì nếu cả 2 tổ cùng làm thì trong 4 ngày hoàn thành công việc nên ta có phương trình \(\dfrac{1}{x} + \dfrac{1}{y} = \dfrac{1}{4}\,\,\left( 1 \right)\).
Vì nếu mỗi tổ làm riêng thì thời gian hoàn thành của tổ I ít hơn thời gian hoàn thành của tố II là 6 ngày nên ta có phương trình \(x + 6 = y\,\,\left( 2 \right)\).
Từ (1) và (2) ta có hệ phương trình: \(\left\{ \begin{array}{l}\dfrac{1}{x} + \dfrac{1}{y} = \dfrac{1}{4}\\x + 6 = y\end{array} \right.\)
\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}\dfrac{1}{x} + \dfrac{1}{{x + 6}} = \dfrac{1}{4}\\x + 6 = y\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\dfrac{{x + 6 + x}}{{x\left( {x + 6} \right)}} = \dfrac{1}{4}\\x + 6 = y\end{array} \right. \Rightarrow \left\{ \begin{array}{l}\dfrac{{2x + 6}}{{x\left( {x + 6} \right)}} = \dfrac{1}{4}\\x + 6 = y\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}8x + 24 = {x^2} + 6x\\x + 6 = y\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x^2} - 2x - 24 = 0\,\,\left( * \right)\\x + 6 = y\end{array} \right.\end{array}\)
Phương trình (*) có \(\Delta ' = {1^2} + 24 = 25 = {5^2} > 0\) nên phương trình (*) có 2 nghiệm phân biệt \(\left[ \begin{array}{l}x = 1 + 5 = 6\,\,\left( {tm} \right)\\x = 1 - 5 = - 4\,\,\left( {ktm} \right)\end{array} \right.\)
Với \(x = 6 \Rightarrow y = x + 6 = 6 + 6 = 12\,\,\left( {tm} \right)\).
Vậy thời gian làm riêng hoàn thành công việc của tổ I, tổ II lần lượt là \(6\) ngày và \(12\) ngày.
Bài 4 (VD)
Phương pháp:
a) Sử dụng tính chất hai tiếp tuyến cắt nhau của đường tròn.
b) Vận dụng dấu hiệu: Tứ giác có góc ngoài bằng góc trong tại đỉnh đối diện là tứ giác nội tiếp.
c) Gọi \(N\) là trung điểm của \(OO'\).
Ta sẽ chứng minh: \(MN//IK\),\(MK//IN\)\( \Rightarrow MNIK\) là hình bình hành (dhnb) \( \Rightarrow MN = IK\) (tính chất hình bình hành).
Mà \(OO' = 2MN\)
Vậy \(OO' = 2IK\,\,\left( {dpcm} \right)\)
Cách giải:
Cho hai đường tròn \(\left( {O;R} \right)\) và \(\left( {O';r} \right)\) tiếp xúc ngoài tại \(A\,\,\left( {R > r} \right)\). Gọi \(BC\) là tiếp tuyến chung ngoài của hai đường tròn này (với \(B \in \left( O \right)\) và \(C \in \left( {O'} \right)\)). Tiếp tuyến chung tại \(A\) của hai đường tròn \(\left( O \right)\) và \(\left( {O'} \right)\) cắt đoạn thẳng \(BC\) tại \(M\).
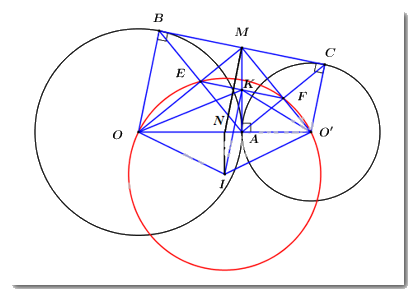
a) Chứng minh \(OM\) vuông góc với \(O'M\).
Theo tính chất 2 tiếp tuyến cắt nhau tại có:
\(MO\) là tia phân giác của \(\angle AMB\) \( \Rightarrow \angle OMA = \dfrac{1}{2}\angle AMB\).
\(MO'\) là tia phân giác của \(\angle AMC\) \( \Rightarrow \angle O'MA = \dfrac{1}{2}\angle AMC\).
\( \Rightarrow \angle OMO' = \angle OAM + \angle O'MA = \dfrac{1}{2}\left( {AMB + \angle AMC} \right) = \dfrac{1}{2}{.180^0} = {90^0}\).
Vậy \(OM \bot O'M\).
b) Gọi \(E\) là giao điểm của \(AB\) với \(OM\) và \(F\) là giao điểm của \(AC\) với \(O'M\). Chứng minh tứ giác \(OEFO'\) nội tiếp một đường tròn.
Ta có: \(MA = MB\) (tính chất 2 tiếp tuyến cắt nhau) \( \Rightarrow M\) thuộc trung trực của \(AB\).
\(OA = OB\,\,\left( { = R} \right)\) \( \Rightarrow O\) thuộc trung trực của \(AB\).
\( \Rightarrow OM\) là trung trực của \(AB\)
\( \Rightarrow OM \bot AB\) tại \(E\).
Chứng minh hoàn toàn tương tự ta có \(O'M \bot AC\) tại \(F\).
Xét tứ giác \(AEMF\) có: \(\angle AEM = \angle AFM = \angle EMF = {90^0}\) \( \Rightarrow AEMF\) là hình chữ nhật (dhnb).
\( \Rightarrow AEMF\) là tứ giác nội tiếp.
\( \Rightarrow \angle MFE = \angle MAE\) (2 góc nội tiếp cùng chắn cung \(ME\)).
Mà \(\angle MAE = \angle MOA\) (cùng phụ với \(\angle OAE\)) \( \Rightarrow \angle MFE = \angle MOA\).
\( \Rightarrow OEFO'\) là tứ giác nội tiếp (tứ giác có góc ngoài bằng góc trong tại đỉnh đối diện).
c) Gọi \(I\) là tâm đường tròn ngoại tiếp tứ giác \(OEFO'\), \(K\) là trung điểm của đoạn \(AM\). Chứng minh \(OO' = 2IK\).
Gọi \(N\) là trung điểm của \(OO'\).
Vì \(\Delta OMO'\) vuông tại \(M\,\,\left( {\angle OMO = {{90}^0}} \right)\,\,\left( {cmt} \right)\) nên \(MN = \dfrac{1}{2}OO' \Rightarrow OO' = 2MN\) (trung tuyến ứng với cạnh huyền trong tam giác vuông bằng nửa cạnh huyền).
Vì \(OM,\,\,O'M\) lần lượt là trung trực của \(AB,\,\,AC\) nên \(E,\,\,F\) lần lượt là trung điểm của \(AB,\,\,AC\).
\( \Rightarrow EF\) là đường trung bình của \(\Delta ABC\) (định nghĩa)
\( \Rightarrow EF = \dfrac{1}{2}BC\) (tính chất đường trung bình của tam giác).
Lại có \(MN\) là đường trung bình của hình thang \(OBCO'\) nên \(MN//OB//O'C\) \( \Rightarrow MN \bot BC\,\,\left( {do\,\,OB \bot BC} \right)\)
Mà \(EF//BC\,\,\left( {cmt} \right) \Rightarrow MN \bot EF\) (từ vuông góc đến song song).
Vì \(K\) là trung điểm của \(AM\), mà \(AEMF\) là hình chữ nhật (cmt) \( \Rightarrow K\) cũng là trung điểm của \(EF\).
\( \Rightarrow IK \bot EF\) (quan hệ vuông góc giữa đường kính và dây cung).
\( \Rightarrow MN//IK\) (từ vuông góc đến song song). (1)
Ta có: \(\left\{ \begin{array}{l}MK \bot OO'\,\,\left( {do\,\,MA \bot OO'} \right)\\IN \bot OO'\end{array} \right. \Rightarrow MK//IN\) (2)
Từ (1) và (2) \( \Rightarrow MNIK\) là hình bình hành (dhnb) \( \Rightarrow MN = IK\) (tính chất hình bình hành).
Mà \(OO' = 2MN\,\,\left( {cmt} \right)\)
Vậy \(OO' = 2IK\,\,\left( {dpcm} \right)\)
Bài 5 (VDC)
Phương pháp:
Ta gắn trục tọa độ của parabol và các điểm M, N vào hệ trục tọa độ \(Oxy\) với \(Oy\) là tia \(OF\) và \(Ox\) là tia thuộc đường thẳng vuông góc với \(OF\) tại \(O\) để giải bài toán.
Cách giải:
Các ăng ten parabol thu sóng hoạt động dựa theo nguyên lý: mọi tia sóng song song với trục của parabol đều có tia phản xạ đi qua tiêu điểm \(F\) của parabol (vì vậy nếu ta đặt thiết bị thu sóng tại \(F\) thì sẽ thu sóng được tốt nhất). Người ta chứng minh được rằng: Nếu đường thẳng vuông góc với trục của parabol tại \(F\) cắt parabol tại 2 điểm \(A,B\) thì \(OF = \dfrac{1}{4}AB\) với \(O\) là đỉnh của parabol (tham khảo hình vẽ).

Tính độ dài đoạn \(OF\)ứng với mô hình trên của một ăng ten parabol (ngang 90cm và cao 9 cm).
Ta gắn trục tọa độ của parabol và các điểm M, N vào hệ trục tọa độ \(Oxy\) với \(Oy\) là tia \(OF\) và \(Ox\) là tia thuộc đường thẳng vuông góc với \(OF\) tại \(O\), khi đó parabol đi qua gốc tọa độ và có dạng \(y = a{x^2}\) và hoành độ của điểm N bằng \(\dfrac{{MN}}{2}\) hay \(N\) có tọa độ là \(N\left( {45;9} \right)\),
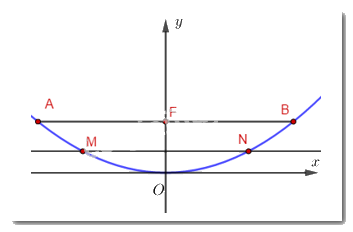
Parabol đi qua hai điểm \(M,N\) nên ta có: \(9 = a{.45^2} \Leftrightarrow a = \dfrac{1}{{225}}\)
\( \Rightarrow \) Parabol là: \(y = \dfrac{1}{{225}}{x^2}\).
Đường thẳng vuông góc với trục của parabol tại \(F\) cắt parabol tại 2 điểm \(A,\,\,B\) nên hai điểm A và B thuộc parabol.
Gọi tọa độ của \(F\) là \(F\left( {0;t} \right)\,\,\left( {t > 0} \right)\), tọa độ của \(B\) là \(B\left( {{x_B},{y_B}} \right)\).
\(OF = \dfrac{1}{4}AB \Rightarrow FB = \dfrac{1}{2}AB = \dfrac{1}{2}.4OF = 2OF = 2t\)\( \Rightarrow {x_B} = FB = 2t\)
\(F,A,B\) cùng thuộc đường thẳng \(AB\) và song song với trục hoành nên có tung độ bằng nhau.
\( \Rightarrow {y_B} = t \Rightarrow B\left( {2t;t} \right)\).
Vì \(B\) là điểm thuộc parabol \(y = \dfrac{1}{{225}}{x^2}\) nên
\(t = \dfrac{1}{{225}}.{\left( {2t} \right)^2} \Leftrightarrow 4{t^2} = 225t \Leftrightarrow 4{t^2} - 225t = 0 \Leftrightarrow t\left( {4t - 225} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}t = 0\,\,\,\,\,\left( {ktm} \right)\\t = \dfrac{{225}}{4}\,\,\left( {tm} \right)\end{array} \right.\)
\( \Rightarrow OF = t = \dfrac{{225}}{4} = 56,25\left( {cm} \right)\)
Vậy \(OF = 56,25cm\).
Kỳ thi tuyển sinh vào lớp 10 môn Toán tại tỉnh Kiên Giang năm 2021 là một bước ngoặt quan trọng trong quá trình học tập của các em học sinh. Đề thi thường bao gồm các dạng bài tập thuộc nhiều chủ đề khác nhau, đòi hỏi học sinh phải có kiến thức vững chắc và kỹ năng giải quyết vấn đề tốt. Việc nắm vững cấu trúc đề thi, các dạng bài tập thường gặp và phương pháp giải quyết hiệu quả là yếu tố then chốt để đạt kết quả cao trong kỳ thi này.
Đề thi vào 10 môn Toán Kiên Giang năm 2021 thường có cấu trúc tương tự như sau:
Các chủ đề thường xuất hiện trong đề thi vào 10 môn Toán Kiên Giang năm 2021 bao gồm:
Để chuẩn bị tốt nhất cho kỳ thi vào 10 môn Toán Kiên Giang năm 2021, các em học sinh cần luyện tập thường xuyên với các đề thi thử và đề thi chính thức của các năm trước. Việc giải đề thi không chỉ giúp các em làm quen với cấu trúc đề thi mà còn giúp các em rèn luyện kỹ năng giải toán, phát hiện ra những lỗ hổng kiến thức và khắc phục chúng kịp thời.
Ngoài bộ đề thi vào 10 môn Toán Kiên Giang năm 2021, các em học sinh có thể tham khảo thêm các tài liệu sau:
Đề thi vào 10 môn Toán Kiên Giang năm 2021 là một kỳ thi quan trọng, đòi hỏi các em học sinh phải có sự chuẩn bị kỹ lưỡng. Hy vọng với bộ đề thi và những lời khuyên trên, các em sẽ tự tin hơn và đạt kết quả tốt nhất trong kỳ thi sắp tới. Chúc các em thành công!