Giaitoan.edu.vn xin giới thiệu bộ đề thi tuyển sinh vào lớp 10 môn Toán tỉnh Hải Dương năm 2019 chính thức. Đây là tài liệu vô cùng quan trọng giúp các em học sinh làm quen với cấu trúc đề thi, rèn luyện kỹ năng giải toán và tự tin hơn trong kỳ thi sắp tới.
Bộ đề thi này bao gồm các đề thi chính thức của các trường THPT chuyên và không chuyên trên địa bàn tỉnh Hải Dương, được biên soạn bởi đội ngũ giáo viên giàu kinh nghiệm của Giaitoan.edu.vn.
Câu 1 (2 điểm) 1) Giải phương trình
Câu 1 (2 điểm)
1) Giải phương trình: \(\sqrt {4{x^2} - 4x + 9} = 3\)
2) Giải hệ phương trình: \(\left\{ \begin{array}{l}3x - y = 5\\2y - x = 0\end{array} \right.\)
Câu 2 (2 điểm)
1) Cho hai đường thẳng \(\left( {{d_1}} \right):y = 2x - 5\) và \(\left( {{d_2}} \right):y = 4x - m\) (m là tham số). Tìm tất cả các giá trị của tham số m để \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) cắt nhau tại một điểm trên trục hoành Ox.
2) Rút gọn biểu thức: \(P = \left( {\dfrac{{\sqrt x }}{{3 + \sqrt x }} + \dfrac{{2x}}{{9 - x}}} \right):\left( {\dfrac{{\sqrt x - 1}}{{x - 3\sqrt x }} - \dfrac{2}{{\sqrt x }}} \right)\) với \(x > 0,\,x \ne 9,\,x \ne 25\)
Câu 3 (2 điểm)
1) Theo kế hoạch, một xưởng may phải may xong 360 bộ quần áo trong một thời gian quy định. Đến khi thực hiện, mỗi ngày xưởng đã may được nhiều hơn 4 bộ quần áo so với số bộ quần áo phải may trong một ngày theo kế hoạch. Vì thế xưởng đã hoàn thành kế hoạch trước 1 ngày. Hỏi theo kế hoạch, mỗi ngày xưởng phải may bao nhiêu bộ quần áo?
2) Cho phương trình: \({x^2} - \left( {2m + 1} \right) - 3 = 0\) (m là tham số). Chứng minh rằng phương trình đã cho luôn có hai nghiệm phân biệt \({x_1},\,{x_2}\) với mọi m. Tìm các giá trị của m sao cho \(\left| {{x_1}} \right| - \left| {{x_2}} \right| = 5\) và \({x_1} < {x_2}\).
Câu 4 (3 điểm) Từ điểm \(A\) nằm ngoài đường tròn \(\left( O \right)\) kẻ 2 tiếp tuyến \(AB,\,\,AC\) với đường tròn (\(B,\,\,C\) là các tiếp điểm). Trên nửa mặt phẳng bờ là đường thẳng \(AO\) chứa điểm \(B\) vẽ cát tuyến \(AMN\) với đường tròn \(\left( O \right)\) (\(AM < AN\), MN không đi qua O). Gọi I là trung điểm của MN.
1) Chứng minh: Tứ giác \(AIOC\) là tứ giác nội tiếp.
2) Gọi H là giao điểm của AO và BC. Chứng minh \(AH.AO = AM.AN\) và tứ giác MNOH là tứ giác nội tiếp.
3) Qua M kẻ đường thẳng song song với BN, cắt AB và BC theo thứ tự tại E và F. Chứng minh rằng M là trung điểm của EF.
Câu 5 (1 điểm) Cho các số dương \(a,b,c\) thỏa mãn điều kiện: \(a + b + c = 2019\)
Tìm giá trị nhỏ nhất của biểu thức: \(P = \sqrt {2{a^2} + ab + 2{b^2}} + \sqrt {2{b^2} + bc + 2{c^2}} + \sqrt {2{c^2} + ca + 2{a^2}.} \)
Câu 1 (2 điểm)
1) Giải phương trình: \(\sqrt {4{x^2} - 4x + 9} = 3\)
2) Giải hệ phương trình: \(\left\{ \begin{array}{l}3x - y = 5\\2y - x = 0\end{array} \right.\)
Câu 2 (2 điểm)
1) Cho hai đường thẳng \(\left( {{d_1}} \right):y = 2x - 5\) và \(\left( {{d_2}} \right):y = 4x - m\) (m là tham số). Tìm tất cả các giá trị của tham số m để \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) cắt nhau tại một điểm trên trục hoành Ox.
2) Rút gọn biểu thức: \(P = \left( {\dfrac{{\sqrt x }}{{3 + \sqrt x }} + \dfrac{{2x}}{{9 - x}}} \right):\left( {\dfrac{{\sqrt x - 1}}{{x - 3\sqrt x }} - \dfrac{2}{{\sqrt x }}} \right)\) với \(x > 0,\,x \ne 9,\,x \ne 25\)
Câu 3 (2 điểm)
1) Theo kế hoạch, một xưởng may phải may xong 360 bộ quần áo trong một thời gian quy định. Đến khi thực hiện, mỗi ngày xưởng đã may được nhiều hơn 4 bộ quần áo so với số bộ quần áo phải may trong một ngày theo kế hoạch. Vì thế xưởng đã hoàn thành kế hoạch trước 1 ngày. Hỏi theo kế hoạch, mỗi ngày xưởng phải may bao nhiêu bộ quần áo?
2) Cho phương trình: \({x^2} - \left( {2m + 1} \right) - 3 = 0\) (m là tham số). Chứng minh rằng phương trình đã cho luôn có hai nghiệm phân biệt \({x_1},\,{x_2}\) với mọi m. Tìm các giá trị của m sao cho \(\left| {{x_1}} \right| - \left| {{x_2}} \right| = 5\) và \({x_1} < {x_2}\).
Câu 4 (3 điểm) Từ điểm \(A\) nằm ngoài đường tròn \(\left( O \right)\) kẻ 2 tiếp tuyến \(AB,\,\,AC\) với đường tròn (\(B,\,\,C\) là các tiếp điểm). Trên nửa mặt phẳng bờ là đường thẳng \(AO\) chứa điểm \(B\) vẽ cát tuyến \(AMN\) với đường tròn \(\left( O \right)\) (\(AM < AN\), MN không đi qua O). Gọi I là trung điểm của MN.
1) Chứng minh: Tứ giác \(AIOC\) là tứ giác nội tiếp.
2) Gọi H là giao điểm của AO và BC. Chứng minh \(AH.AO = AM.AN\) và tứ giác MNOH là tứ giác nội tiếp.
3) Qua M kẻ đường thẳng song song với BN, cắt AB và BC theo thứ tự tại E và F. Chứng minh rằng M là trung điểm của EF.
Câu 5 (1 điểm) Cho các số dương \(a,b,c\) thỏa mãn điều kiện: \(a + b + c = 2019\)
Tìm giá trị nhỏ nhất của biểu thức: \(P = \sqrt {2{a^2} + ab + 2{b^2}} + \sqrt {2{b^2} + bc + 2{c^2}} + \sqrt {2{c^2} + ca + 2{a^2}.} \)
Câu 1 (2 điểm):
Phương pháp:
1) Giải phương trình bằng phương pháp bình phương hai vế sau đó giải phương trình bậc hai.
2) Giải hệ phương trình bằng phương pháp thế hoặc phương pháp cộng đại số.
Cách giải:
1) Giải phương trình: \(\sqrt {4{x^2} - 4x + 9} = 3\).
ĐKXĐ: \(4{x^2} - 4x + 9 \ge 0 \Leftrightarrow 4{x^2} - 4x + 1 + 8 \ge 0 \Leftrightarrow {\left( {2x - 1} \right)^2} + 8 \ge 0\) (luôn đúng).
\(\begin{array}{l}\sqrt {4{x^2} - 4x + 9} = 3 \Leftrightarrow 4{x^2} - 4x + 9 = 9\\ \Leftrightarrow 4{x^2} - 4x = 0 \Leftrightarrow 4x\left( {x - 1} \right) = 0\\ \Rightarrow \left[ \begin{array}{l}x = 0\\x - 1 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 1\end{array} \right.\end{array}\)
Vậy tập nghiệm của phương trình là: \(S = \left\{ {0;1} \right\}\)
2) Giải hệ phương trình: \(\left\{ \begin{array}{l}3x - y = 5\\2y - x = 0\end{array} \right.\)
\(\left\{ \begin{array}{l}3x - y = 5\\2y - x = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}3x - y = 5\\ - x + 2y = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}3x - y = 5\\ - 3x + 6y = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}5y = 5\\x = 2y\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 1\end{array} \right.\)
Vậy nghiệm của hệ phương trình là: \(\left( {x;y} \right) = \left( {2;1} \right)\).
Câu 2 (2,0 điểm):
Phương pháp:
1) Tìm giao điểm của \({d_1}\) với trục hoành.
Thay tọa độ giao điểm đó vào công thức đường thẳng \({d_2}\) để tìm \(m.\)
2) Quy đồng mẫu các phân thức, biến đổi và rút gọn biểu thức.
Cách giải:
1) Cho hai đường thẳng \(\left( {{d_1}} \right):y = 2x - 5\) và \(\left( {{d_2}} \right):y = 4x - m\) (m là tham số). Tìm tất cả các giá trị của tham số m để \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) cắt nhau tại một điểm trên trục hoành Ox.
Phương trình hoành độ giao điểm của \({d_1}\) với \(Ox\) là: \(2x - 5 = 0 \Leftrightarrow x = \dfrac{5}{2}\)
\( \Rightarrow \) Giao điểm của \(\left( {{d_1}} \right),\,\,\left( {{d_2}} \right)\) thuộc trục hoành là: \(M\left( {\dfrac{5}{2};0} \right)\)
Vì \(M\left( {\dfrac{5}{2};0} \right) \in \left( {{d_2}} \right)\)nên ta có: \(0 = 4.\dfrac{5}{2} - m \Rightarrow m = 10.\)
Vậy với \(m = 10\) thì \({d_1};\,{d_2}\) cắt nhau tại một điểm trên trục hoành Ox.
2) Rút gọn biểu thức: \(P = \left( {\dfrac{{\sqrt x }}{{3 + \sqrt x }} + \dfrac{{2x}}{{9 - x}}} \right):\left( {\dfrac{{\sqrt x - 1}}{{x - 3\sqrt x }} - \dfrac{2}{{\sqrt x }}} \right)\) với \(x > 0,\,\,\,x \ne 9,\,\,\,x \ne 25\)
Với \(x > 0,\,\,\,x \ne 9,\,\,\,x \ne 25\)ta có:
\(\begin{array}{l}P = \left( {\dfrac{{\sqrt x }}{{3 + \sqrt x }} + \dfrac{{2x}}{{9 - x}}} \right):\left( {\dfrac{{\sqrt x - 1}}{{x - 3\sqrt x }} - \dfrac{2}{{\sqrt x }}} \right)\\ = \left( {\dfrac{{\sqrt x }}{{3 + \sqrt x }} + \dfrac{{2x}}{{\left( {3 + \sqrt x } \right)\left( {3 - \sqrt x } \right)}}} \right):\left( {\dfrac{{\sqrt x - 1}}{{\sqrt x \left( {\sqrt x - 3} \right)}} - \dfrac{2}{{\sqrt x }}} \right)\\ = \dfrac{{\sqrt x \left( {3 - \sqrt x } \right) + 2x}}{{\left( {3 + \sqrt x } \right)\left( {3 - \sqrt x } \right)}}:\dfrac{{\sqrt x - 1 - 2.\left( {\sqrt x - 3} \right)}}{{\sqrt x \left( {\sqrt x - 3} \right)}}\\ = \dfrac{{3\sqrt x - x + 2x}}{{\left( {3 + \sqrt x } \right)\left( {3 - \sqrt x } \right)}}:\dfrac{{\sqrt x - 1 - 2\sqrt x + 6}}{{\sqrt {x.} \left( {\sqrt x - 3} \right)}}\\ = \dfrac{{3\sqrt x + x}}{{\left( {3 + \sqrt x } \right)\left( {3 - \sqrt x } \right)}}:\dfrac{{ - \sqrt x + 5}}{{\sqrt x .\left( {\sqrt x - 3} \right)}}\\ = \dfrac{{\sqrt x \left( {3 + \sqrt x } \right)}}{{\left( {3 + \sqrt x } \right)\left( {3 - \sqrt x } \right)}}.\dfrac{{\sqrt x \left( {3 - \sqrt x } \right)}}{{\sqrt x - 5}}\\ = \dfrac{x}{{\sqrt x - 5}}\end{array}\)
Vậy \(P = \dfrac{x}{{\sqrt x - 5}}\).
Câu 3 (2,0 điểm):
Phương pháp:
1) Giải bài toán bằng cách lập phương trình:
Gọi số bộ quần áo mỗi ngày xưởng phải may theo kế hoạch là x (bộ) \(\left( {x \in {N^*},\,x < 360} \right).\)
Biểu diễn các đại lượng chưa biết theo các đại lượng đã biết và ẩn vừa gọi.
Dựa vào các giả thiết để lập phương trình. Giải phương trình tìm ẩn.
Đối chiếu với điều kiện của ẩn rồi kết luận.
2) Phương trình có hai nghiệm phân biệt \( \Leftrightarrow \Delta > 0.\)
Áp dụng hệ thức Vi-ét và biểu thức bài cho để tìm \(m.\) Đối chiếu với điều kiện rồi kết luận.
Cách giải:
1) Gọi số bộ quần áo mỗi ngày xưởng phải may theo kế hoạch là x (bộ) \(\left( {x \in {N^*},\,x < 360} \right).\)
Thời gian may xong 360 bộ quần áo theo kế hoạch là: \(\dfrac{{360}}{x}\) (ngày).
Đến khi thực hiện, mỗi ngày xưởng đã may được nhiều hơn 4 bộ quần áo so với số bộ quần áo phải may trong một ngày theo kế hoạch nên mỗi ngày thực tế may được \(x + 4\) (bộ).
Thời gian may xong 360 bộ quần áo theo thực tế là: \(\dfrac{{360}}{{x + 4}}\) (ngày).
Vì xưởng đã hoàn thành kế hoạch trước 1 ngày nên ta có phương trình:
\(\begin{array}{l}\,\,\,\,\,\,\dfrac{{360}}{x} - \dfrac{{360}}{{x + 4}} = 1 \Leftrightarrow \dfrac{1}{x} - \dfrac{1}{{x + 4}} = \dfrac{1}{{360}}\\ \Leftrightarrow \dfrac{4}{{x\left( {x + 4} \right)}} = \dfrac{1}{{360}} \Leftrightarrow x\left( {x + 4} \right) = 1440\\ \Leftrightarrow {x^2} + 4x - 1440 = 0 \Leftrightarrow {x^2} - 36x + 40x - 1440 = 0\\ \Leftrightarrow x\left( {x - 36} \right) + 40\left( {x - 36} \right) = 0 \Leftrightarrow \left( {x - 36} \right)\left( {x + 40} \right) = 0\\ \Rightarrow \left[ \begin{array}{l}x = 36\,\,\,\,\,\,\left( {tm} \right)\\x = - 40\,\,\,\left( {ktm} \right)\end{array} \right.\end{array}\)
Vậy theo kế hoạch, mỗi ngày xưởng phải may 36 bộ quần áo.
2) Cho phương trình: \({x^2} - \left( {2m + 1} \right) - 3 = 0\) (m là tham số). Chứng minh rằng phương trình đã cho luôn có hai nghiệm phân biệt \({x_1},\,{x_2}\) với mọi m. Tìm các giá trị của m sao cho \(\left| {{x_1}} \right| - \left| {{x_2}} \right| = 5\) và \({x_1} < {x_2}\).
Ta có \(\Delta = {\left( {2m + 1} \right)^2} - 4.1.\left( { - 3} \right) = {\left( {2m + 1} \right)^2} + 12\).
Ta có \({\left( {2m + 1} \right)^2} \ge 0\,\,\forall m \Leftrightarrow {\left( {2m + 1} \right)^2} + 12 \ge 1 > 0\,\,\forall m \Rightarrow \) Phương trình đã cho luôn có 2 nghiệm phân biệt \({x_1};\,\,{x_2}\,\,\left( {{x_1} < {x_2}} \right)\) với mọi giá trị của m.
Khi đó áp dụng định lí Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2m + 1\\{x_1}{x_2} = - 3\end{array} \right.\).
Do \({x_1}{x_2} = - 3 < 0 \Rightarrow {x_1},\,\,{x_2}\) trái dấu. Mà \({x_1} < {x_2}\,\,\left( {gt} \right) \Rightarrow {x_1} < 0 < {x_2} \Rightarrow \left\{ \begin{array}{l}\left| {{x_1}} \right| = - {x_1}\\\left| {{x_2}} \right| = {x_2}\end{array} \right.\).
Theo bài ra ta có: \(\left| {{x_1}} \right| - \left| {{x_2}} \right| = 5 \Leftrightarrow - {x_1} - {x_2} = 5 \Leftrightarrow {x_1} + {x_2} = - 5\).
Mà \({x_1} + {x_2} = 2m + 1 \Rightarrow - 5 = 2m + 1 \Leftrightarrow 2m = - 6 \Leftrightarrow m = - 3.\)
Vậy \(m = - 3\) thỏa mãn yêu cầu bài toán.
Câu 4
Phương pháp:
1) Chứng minh tứ giác nội tiếp nhờ các dấu hiệu nhận biết.
2) Chứng minh các cặp tam giác đồng dạng từ đó suy ra đẳng thức đề bài yêu cầu.
+) Từ các tam giác giác đồng dạng suy ra cặp góc tương ứng bằng nhau, từ đó chứng minh tứ giác nội tiếp theo dấu hiệu nhận biết.
3) Sử dụng tính chất của tia phân giác.
Cách giải:
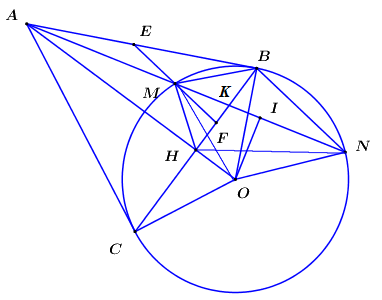
1) Chứng minh: Tứ giác \(AIOC\) là tứ giác nội tiếp.
Do \(I\) là trung điểm của \(MN \Rightarrow OI \bot MN \Rightarrow \angle OIA = {90^0}\).
Xét tứ giác \(AIOC\) có \(\angle OIA + \angle OCA = {90^0} + {90^0} = {180^0} \Rightarrow \) Tứ giác \(AIOC\) là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng 1800).
2) Gọi H là giao điểm của AO và BC. Chứng minh \(AH.AO = AM.AN\) và tứ giác MNOH là tứ giác nội tiếp.
Xét tam giác \(ABM\) và tam giác \(ANB\) có:
\(\angle BAN\) chung;
\(\angle ABM = \angle ANB\) (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung \(BM\));
.
Ta có: \(OB = OC\,\,\left( { = R} \right) \Rightarrow O\) thuộc trung trực của \(BC\).
\(AB = AC\) (Tính chất 2 tiếp tuyến cắt nhau) \( \Rightarrow A\) thuộc trung trực của \(BC\).
\( \Rightarrow OA\) là trung trực của \(BC \Rightarrow OA \bot BC\) tại H.
Áp dụng hệ thức lượng trong tam giác vuông OAB (đường cao OH) ta có: \(A{B^2} = AH.AO\,\,\,\left( 2 \right)\).
Từ (1) và (2) suy ra: \(AH.AO = AM.AN\).
\(AH.AO = AM.AN \Rightarrow \dfrac{{AM}}{{AH}} = \dfrac{{AO}}{{AN}}\).
Xét tam giác \(AMH\) và tam giác \(AON\) có:
\(\angle OAN\) chung;
\(\dfrac{{AM}}{{AH}} = \dfrac{{AO}}{{AN}}\,\,\left( {cmt} \right)\);
.
\( \Rightarrow \) Tứ giác MNOH là tứ giác nội tiếp (Tứ giác có góc ngoài tại 1 đỉnh bằng góc trong tại đỉnh đối diện).
3) Qua M kẻ đường thẳng song song với BN, cắt AB và BC theo thứ tự tại E và F. Chứng minh rằng M là trung điểm của EF.
Gọi \(K = AN \cap BC\).
Tứ giác MNOH là tứ giác nội tiếp (cmt) \( \Rightarrow \angle OHN = \angle OMN\) (hai góc nội tiếp cùng chắn cung ON).
Mà \(OM = ON \Rightarrow \Delta OMN\) cân tại \(O \Rightarrow \angle OMN = \angle ONM\).
\( \Rightarrow \angle OHN = \angle ONM\).
Lại có \(\angle ONM = \angle AHM\) (góc ngoài và góc trong tại đỉnh đối diện của tứ giác nội tiếp).
\( \Rightarrow \angle OHN = \angle AHM \Rightarrow {90^0} - \angle OHN = {90^0} - \angle AHM \Rightarrow \angle NHB = \angle MHB\).
\( \Rightarrow HB\) là phân giác trong của \(\angle MHN\), mà \(AH \bot HB\,\,\left( {OA \bot BC} \right) \Rightarrow AH\) là phân giác ngoài của \(\angle MHN\).
Áp dụng tính chất đường phân giác ta có : \(\dfrac{{HM}}{{HN}} = \dfrac{{KM}}{{KN}} = \dfrac{{AM}}{{AN}}\,\,\left( 3 \right)\).
Do \(MF//BN \Rightarrow \) Áp dụng định lí Ta-lét ta có : \(\dfrac{{MF}}{{BN}} = \dfrac{{KM}}{{KN}};\,\,\dfrac{{AM}}{{AN}} = \dfrac{{ME}}{{BN}}\,\,\,\left( 4 \right)\).
Từ (3) và (4) \( \Rightarrow \dfrac{{ME}}{{BN}} = \dfrac{{MF}}{{BN}} \Rightarrow ME = MF\).
Vậy \(M\) là trung điểm của \(EF\,\,\left( {dpcm} \right)\).
Câu 5 (1,0 điểm):
Phương pháp:
Áp dụng bất đẳng thức Cô-si để làm bài toán.
Cách giải:
Ta có: \(2{a^2} + ab + 2{b^2} = \dfrac{{{a^2} + 2ab + {b^2}}}{2} + \dfrac{{3{a^2} + 3{b^2}}}{2} = \dfrac{{{{\left( {a + b} \right)}^2}}}{2} + \dfrac{{3\left( {{a^2} + {b^2}} \right)}}{2}\).
Mà \({a^2} + {b^2} \ge \dfrac{{{{\left( {a + b} \right)}^2}}}{2} \Leftrightarrow \dfrac{{3\left( {{a^2} + {b^2}} \right)}}{2} \ge \dfrac{3}{2}\dfrac{{{{\left( {a + b} \right)}^2}}}{2} = \dfrac{{3{{\left( {a + b} \right)}^2}}}{4}\).
\(\begin{array}{l} \Rightarrow 2{a^2} + ab + 2{b^2} \ge \dfrac{{{{\left( {a + b} \right)}^2}}}{2} + \dfrac{{3{{\left( {a + b} \right)}^2}}}{4} = \dfrac{{5{{\left( {a + b} \right)}^2}}}{4}\\ \Rightarrow \sqrt {2{a^2} + ab + 2{b^2}} \ge \dfrac{{\sqrt 5 }}{2}\left( {a + b} \right)\end{array}\).
Chứng minh tương tự ta có:
\(\begin{array}{l}\sqrt {2{b^2} + bc + 2{c^2}} \ge \dfrac{{\sqrt 5 }}{2}\left( {b + c} \right)\\\sqrt {2{c^2} + ca + 2{a^2}} \ge \dfrac{{\sqrt 5 }}{2}\left( {c + a} \right)\end{array}\)
Cộng vế theo vế ta có:
\(\begin{array}{l}P = \sqrt {2{a^2} + ab + 2{b^2}} + \sqrt {2{b^2} + bc + 2{c^2}} + \sqrt {2{c^2} + ca + 2{a^2}} \\\,\,\,\,\, \ge \dfrac{{\sqrt 5 }}{2}\left( {a + b + b + c + c + a} \right) = \sqrt 5 \left( {a + b + c} \right) = 2019\sqrt 5 \end{array}\)
Dấu “=” xảy ra \( \Leftrightarrow \left\{ \begin{array}{l}a = b = c\\a + b + c = 2019\end{array} \right. \Leftrightarrow a = b = c = \dfrac{{2019}}{3}\).
Câu 1 (2 điểm):
Phương pháp:
1) Giải phương trình bằng phương pháp bình phương hai vế sau đó giải phương trình bậc hai.
2) Giải hệ phương trình bằng phương pháp thế hoặc phương pháp cộng đại số.
Cách giải:
1) Giải phương trình: \(\sqrt {4{x^2} - 4x + 9} = 3\).
ĐKXĐ: \(4{x^2} - 4x + 9 \ge 0 \Leftrightarrow 4{x^2} - 4x + 1 + 8 \ge 0 \Leftrightarrow {\left( {2x - 1} \right)^2} + 8 \ge 0\) (luôn đúng).
\(\begin{array}{l}\sqrt {4{x^2} - 4x + 9} = 3 \Leftrightarrow 4{x^2} - 4x + 9 = 9\\ \Leftrightarrow 4{x^2} - 4x = 0 \Leftrightarrow 4x\left( {x - 1} \right) = 0\\ \Rightarrow \left[ \begin{array}{l}x = 0\\x - 1 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 1\end{array} \right.\end{array}\)
Vậy tập nghiệm của phương trình là: \(S = \left\{ {0;1} \right\}\)
2) Giải hệ phương trình: \(\left\{ \begin{array}{l}3x - y = 5\\2y - x = 0\end{array} \right.\)
\(\left\{ \begin{array}{l}3x - y = 5\\2y - x = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}3x - y = 5\\ - x + 2y = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}3x - y = 5\\ - 3x + 6y = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}5y = 5\\x = 2y\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 1\end{array} \right.\)
Vậy nghiệm của hệ phương trình là: \(\left( {x;y} \right) = \left( {2;1} \right)\).
Câu 2 (2,0 điểm):
Phương pháp:
1) Tìm giao điểm của \({d_1}\) với trục hoành.
Thay tọa độ giao điểm đó vào công thức đường thẳng \({d_2}\) để tìm \(m.\)
2) Quy đồng mẫu các phân thức, biến đổi và rút gọn biểu thức.
Cách giải:
1) Cho hai đường thẳng \(\left( {{d_1}} \right):y = 2x - 5\) và \(\left( {{d_2}} \right):y = 4x - m\) (m là tham số). Tìm tất cả các giá trị của tham số m để \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) cắt nhau tại một điểm trên trục hoành Ox.
Phương trình hoành độ giao điểm của \({d_1}\) với \(Ox\) là: \(2x - 5 = 0 \Leftrightarrow x = \dfrac{5}{2}\)
\( \Rightarrow \) Giao điểm của \(\left( {{d_1}} \right),\,\,\left( {{d_2}} \right)\) thuộc trục hoành là: \(M\left( {\dfrac{5}{2};0} \right)\)
Vì \(M\left( {\dfrac{5}{2};0} \right) \in \left( {{d_2}} \right)\)nên ta có: \(0 = 4.\dfrac{5}{2} - m \Rightarrow m = 10.\)
Vậy với \(m = 10\) thì \({d_1};\,{d_2}\) cắt nhau tại một điểm trên trục hoành Ox.
2) Rút gọn biểu thức: \(P = \left( {\dfrac{{\sqrt x }}{{3 + \sqrt x }} + \dfrac{{2x}}{{9 - x}}} \right):\left( {\dfrac{{\sqrt x - 1}}{{x - 3\sqrt x }} - \dfrac{2}{{\sqrt x }}} \right)\) với \(x > 0,\,\,\,x \ne 9,\,\,\,x \ne 25\)
Với \(x > 0,\,\,\,x \ne 9,\,\,\,x \ne 25\)ta có:
\(\begin{array}{l}P = \left( {\dfrac{{\sqrt x }}{{3 + \sqrt x }} + \dfrac{{2x}}{{9 - x}}} \right):\left( {\dfrac{{\sqrt x - 1}}{{x - 3\sqrt x }} - \dfrac{2}{{\sqrt x }}} \right)\\ = \left( {\dfrac{{\sqrt x }}{{3 + \sqrt x }} + \dfrac{{2x}}{{\left( {3 + \sqrt x } \right)\left( {3 - \sqrt x } \right)}}} \right):\left( {\dfrac{{\sqrt x - 1}}{{\sqrt x \left( {\sqrt x - 3} \right)}} - \dfrac{2}{{\sqrt x }}} \right)\\ = \dfrac{{\sqrt x \left( {3 - \sqrt x } \right) + 2x}}{{\left( {3 + \sqrt x } \right)\left( {3 - \sqrt x } \right)}}:\dfrac{{\sqrt x - 1 - 2.\left( {\sqrt x - 3} \right)}}{{\sqrt x \left( {\sqrt x - 3} \right)}}\\ = \dfrac{{3\sqrt x - x + 2x}}{{\left( {3 + \sqrt x } \right)\left( {3 - \sqrt x } \right)}}:\dfrac{{\sqrt x - 1 - 2\sqrt x + 6}}{{\sqrt {x.} \left( {\sqrt x - 3} \right)}}\\ = \dfrac{{3\sqrt x + x}}{{\left( {3 + \sqrt x } \right)\left( {3 - \sqrt x } \right)}}:\dfrac{{ - \sqrt x + 5}}{{\sqrt x .\left( {\sqrt x - 3} \right)}}\\ = \dfrac{{\sqrt x \left( {3 + \sqrt x } \right)}}{{\left( {3 + \sqrt x } \right)\left( {3 - \sqrt x } \right)}}.\dfrac{{\sqrt x \left( {3 - \sqrt x } \right)}}{{\sqrt x - 5}}\\ = \dfrac{x}{{\sqrt x - 5}}\end{array}\)
Vậy \(P = \dfrac{x}{{\sqrt x - 5}}\).
Câu 3 (2,0 điểm):
Phương pháp:
1) Giải bài toán bằng cách lập phương trình:
Gọi số bộ quần áo mỗi ngày xưởng phải may theo kế hoạch là x (bộ) \(\left( {x \in {N^*},\,x < 360} \right).\)
Biểu diễn các đại lượng chưa biết theo các đại lượng đã biết và ẩn vừa gọi.
Dựa vào các giả thiết để lập phương trình. Giải phương trình tìm ẩn.
Đối chiếu với điều kiện của ẩn rồi kết luận.
2) Phương trình có hai nghiệm phân biệt \( \Leftrightarrow \Delta > 0.\)
Áp dụng hệ thức Vi-ét và biểu thức bài cho để tìm \(m.\) Đối chiếu với điều kiện rồi kết luận.
Cách giải:
1) Gọi số bộ quần áo mỗi ngày xưởng phải may theo kế hoạch là x (bộ) \(\left( {x \in {N^*},\,x < 360} \right).\)
Thời gian may xong 360 bộ quần áo theo kế hoạch là: \(\dfrac{{360}}{x}\) (ngày).
Đến khi thực hiện, mỗi ngày xưởng đã may được nhiều hơn 4 bộ quần áo so với số bộ quần áo phải may trong một ngày theo kế hoạch nên mỗi ngày thực tế may được \(x + 4\) (bộ).
Thời gian may xong 360 bộ quần áo theo thực tế là: \(\dfrac{{360}}{{x + 4}}\) (ngày).
Vì xưởng đã hoàn thành kế hoạch trước 1 ngày nên ta có phương trình:
\(\begin{array}{l}\,\,\,\,\,\,\dfrac{{360}}{x} - \dfrac{{360}}{{x + 4}} = 1 \Leftrightarrow \dfrac{1}{x} - \dfrac{1}{{x + 4}} = \dfrac{1}{{360}}\\ \Leftrightarrow \dfrac{4}{{x\left( {x + 4} \right)}} = \dfrac{1}{{360}} \Leftrightarrow x\left( {x + 4} \right) = 1440\\ \Leftrightarrow {x^2} + 4x - 1440 = 0 \Leftrightarrow {x^2} - 36x + 40x - 1440 = 0\\ \Leftrightarrow x\left( {x - 36} \right) + 40\left( {x - 36} \right) = 0 \Leftrightarrow \left( {x - 36} \right)\left( {x + 40} \right) = 0\\ \Rightarrow \left[ \begin{array}{l}x = 36\,\,\,\,\,\,\left( {tm} \right)\\x = - 40\,\,\,\left( {ktm} \right)\end{array} \right.\end{array}\)
Vậy theo kế hoạch, mỗi ngày xưởng phải may 36 bộ quần áo.
2) Cho phương trình: \({x^2} - \left( {2m + 1} \right) - 3 = 0\) (m là tham số). Chứng minh rằng phương trình đã cho luôn có hai nghiệm phân biệt \({x_1},\,{x_2}\) với mọi m. Tìm các giá trị của m sao cho \(\left| {{x_1}} \right| - \left| {{x_2}} \right| = 5\) và \({x_1} < {x_2}\).
Ta có \(\Delta = {\left( {2m + 1} \right)^2} - 4.1.\left( { - 3} \right) = {\left( {2m + 1} \right)^2} + 12\).
Ta có \({\left( {2m + 1} \right)^2} \ge 0\,\,\forall m \Leftrightarrow {\left( {2m + 1} \right)^2} + 12 \ge 1 > 0\,\,\forall m \Rightarrow \) Phương trình đã cho luôn có 2 nghiệm phân biệt \({x_1};\,\,{x_2}\,\,\left( {{x_1} < {x_2}} \right)\) với mọi giá trị của m.
Khi đó áp dụng định lí Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2m + 1\\{x_1}{x_2} = - 3\end{array} \right.\).
Do \({x_1}{x_2} = - 3 < 0 \Rightarrow {x_1},\,\,{x_2}\) trái dấu. Mà \({x_1} < {x_2}\,\,\left( {gt} \right) \Rightarrow {x_1} < 0 < {x_2} \Rightarrow \left\{ \begin{array}{l}\left| {{x_1}} \right| = - {x_1}\\\left| {{x_2}} \right| = {x_2}\end{array} \right.\).
Theo bài ra ta có: \(\left| {{x_1}} \right| - \left| {{x_2}} \right| = 5 \Leftrightarrow - {x_1} - {x_2} = 5 \Leftrightarrow {x_1} + {x_2} = - 5\).
Mà \({x_1} + {x_2} = 2m + 1 \Rightarrow - 5 = 2m + 1 \Leftrightarrow 2m = - 6 \Leftrightarrow m = - 3.\)
Vậy \(m = - 3\) thỏa mãn yêu cầu bài toán.
Câu 4
Phương pháp:
1) Chứng minh tứ giác nội tiếp nhờ các dấu hiệu nhận biết.
2) Chứng minh các cặp tam giác đồng dạng từ đó suy ra đẳng thức đề bài yêu cầu.
+) Từ các tam giác giác đồng dạng suy ra cặp góc tương ứng bằng nhau, từ đó chứng minh tứ giác nội tiếp theo dấu hiệu nhận biết.
3) Sử dụng tính chất của tia phân giác.
Cách giải:
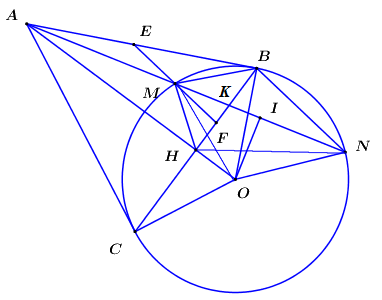
1) Chứng minh: Tứ giác \(AIOC\) là tứ giác nội tiếp.
Do \(I\) là trung điểm của \(MN \Rightarrow OI \bot MN \Rightarrow \angle OIA = {90^0}\).
Xét tứ giác \(AIOC\) có \(\angle OIA + \angle OCA = {90^0} + {90^0} = {180^0} \Rightarrow \) Tứ giác \(AIOC\) là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng 1800).
2) Gọi H là giao điểm của AO và BC. Chứng minh \(AH.AO = AM.AN\) và tứ giác MNOH là tứ giác nội tiếp.
Xét tam giác \(ABM\) và tam giác \(ANB\) có:
\(\angle BAN\) chung;
\(\angle ABM = \angle ANB\) (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung \(BM\));
.
Ta có: \(OB = OC\,\,\left( { = R} \right) \Rightarrow O\) thuộc trung trực của \(BC\).
\(AB = AC\) (Tính chất 2 tiếp tuyến cắt nhau) \( \Rightarrow A\) thuộc trung trực của \(BC\).
\( \Rightarrow OA\) là trung trực của \(BC \Rightarrow OA \bot BC\) tại H.
Áp dụng hệ thức lượng trong tam giác vuông OAB (đường cao OH) ta có: \(A{B^2} = AH.AO\,\,\,\left( 2 \right)\).
Từ (1) và (2) suy ra: \(AH.AO = AM.AN\).
\(AH.AO = AM.AN \Rightarrow \dfrac{{AM}}{{AH}} = \dfrac{{AO}}{{AN}}\).
Xét tam giác \(AMH\) và tam giác \(AON\) có:
\(\angle OAN\) chung;
\(\dfrac{{AM}}{{AH}} = \dfrac{{AO}}{{AN}}\,\,\left( {cmt} \right)\);
.
\( \Rightarrow \) Tứ giác MNOH là tứ giác nội tiếp (Tứ giác có góc ngoài tại 1 đỉnh bằng góc trong tại đỉnh đối diện).
3) Qua M kẻ đường thẳng song song với BN, cắt AB và BC theo thứ tự tại E và F. Chứng minh rằng M là trung điểm của EF.
Gọi \(K = AN \cap BC\).
Tứ giác MNOH là tứ giác nội tiếp (cmt) \( \Rightarrow \angle OHN = \angle OMN\) (hai góc nội tiếp cùng chắn cung ON).
Mà \(OM = ON \Rightarrow \Delta OMN\) cân tại \(O \Rightarrow \angle OMN = \angle ONM\).
\( \Rightarrow \angle OHN = \angle ONM\).
Lại có \(\angle ONM = \angle AHM\) (góc ngoài và góc trong tại đỉnh đối diện của tứ giác nội tiếp).
\( \Rightarrow \angle OHN = \angle AHM \Rightarrow {90^0} - \angle OHN = {90^0} - \angle AHM \Rightarrow \angle NHB = \angle MHB\).
\( \Rightarrow HB\) là phân giác trong của \(\angle MHN\), mà \(AH \bot HB\,\,\left( {OA \bot BC} \right) \Rightarrow AH\) là phân giác ngoài của \(\angle MHN\).
Áp dụng tính chất đường phân giác ta có : \(\dfrac{{HM}}{{HN}} = \dfrac{{KM}}{{KN}} = \dfrac{{AM}}{{AN}}\,\,\left( 3 \right)\).
Do \(MF//BN \Rightarrow \) Áp dụng định lí Ta-lét ta có : \(\dfrac{{MF}}{{BN}} = \dfrac{{KM}}{{KN}};\,\,\dfrac{{AM}}{{AN}} = \dfrac{{ME}}{{BN}}\,\,\,\left( 4 \right)\).
Từ (3) và (4) \( \Rightarrow \dfrac{{ME}}{{BN}} = \dfrac{{MF}}{{BN}} \Rightarrow ME = MF\).
Vậy \(M\) là trung điểm của \(EF\,\,\left( {dpcm} \right)\).
Câu 5 (1,0 điểm):
Phương pháp:
Áp dụng bất đẳng thức Cô-si để làm bài toán.
Cách giải:
Ta có: \(2{a^2} + ab + 2{b^2} = \dfrac{{{a^2} + 2ab + {b^2}}}{2} + \dfrac{{3{a^2} + 3{b^2}}}{2} = \dfrac{{{{\left( {a + b} \right)}^2}}}{2} + \dfrac{{3\left( {{a^2} + {b^2}} \right)}}{2}\).
Mà \({a^2} + {b^2} \ge \dfrac{{{{\left( {a + b} \right)}^2}}}{2} \Leftrightarrow \dfrac{{3\left( {{a^2} + {b^2}} \right)}}{2} \ge \dfrac{3}{2}\dfrac{{{{\left( {a + b} \right)}^2}}}{2} = \dfrac{{3{{\left( {a + b} \right)}^2}}}{4}\).
\(\begin{array}{l} \Rightarrow 2{a^2} + ab + 2{b^2} \ge \dfrac{{{{\left( {a + b} \right)}^2}}}{2} + \dfrac{{3{{\left( {a + b} \right)}^2}}}{4} = \dfrac{{5{{\left( {a + b} \right)}^2}}}{4}\\ \Rightarrow \sqrt {2{a^2} + ab + 2{b^2}} \ge \dfrac{{\sqrt 5 }}{2}\left( {a + b} \right)\end{array}\).
Chứng minh tương tự ta có:
\(\begin{array}{l}\sqrt {2{b^2} + bc + 2{c^2}} \ge \dfrac{{\sqrt 5 }}{2}\left( {b + c} \right)\\\sqrt {2{c^2} + ca + 2{a^2}} \ge \dfrac{{\sqrt 5 }}{2}\left( {c + a} \right)\end{array}\)
Cộng vế theo vế ta có:
\(\begin{array}{l}P = \sqrt {2{a^2} + ab + 2{b^2}} + \sqrt {2{b^2} + bc + 2{c^2}} + \sqrt {2{c^2} + ca + 2{a^2}} \\\,\,\,\,\, \ge \dfrac{{\sqrt 5 }}{2}\left( {a + b + b + c + c + a} \right) = \sqrt 5 \left( {a + b + c} \right) = 2019\sqrt 5 \end{array}\)
Dấu “=” xảy ra \( \Leftrightarrow \left\{ \begin{array}{l}a = b = c\\a + b + c = 2019\end{array} \right. \Leftrightarrow a = b = c = \dfrac{{2019}}{3}\).
Kỳ thi tuyển sinh vào lớp 10 môn Toán tại Hải Dương năm 2019 được đánh giá là một kỳ thi có độ khó vừa phải, tập trung vào các kiến thức cơ bản của chương trình Toán THCS. Tuy nhiên, để đạt được kết quả cao, học sinh cần có sự chuẩn bị kỹ lưỡng và nắm vững các kỹ năng giải toán quan trọng.
Đề thi thường bao gồm các dạng bài tập sau:
Đề thi trường THPT Chuyên Nguyễn Trãi thường có độ khó cao hơn so với các trường khác. Đề thi năm 2019 tập trung vào các bài toán đại số phức tạp và các bài toán hình học đòi hỏi tư duy sáng tạo. Một số câu hỏi yêu cầu học sinh phải vận dụng kiến thức từ nhiều chương khác nhau để giải quyết.
Đề thi trường THPT Hùng Vương có độ khó trung bình, tập trung vào các kiến thức cơ bản và các kỹ năng giải toán thông thường. Đề thi năm 2019 có nhiều câu hỏi về đại số và hình học, yêu cầu học sinh phải nắm vững các công thức và định lý cơ bản.
Dạng 1: Giải phương trình bậc hai
Để giải phương trình bậc hai, học sinh cần sử dụng công thức nghiệm hoặc phương pháp phân tích thành nhân tử. Ví dụ:
x2 - 5x + 6 = 0
(x - 2)(x - 3) = 0
Vậy x = 2 hoặc x = 3
Dạng 2: Tính diện tích hình học
Để tính diện tích hình học, học sinh cần nắm vững các công thức tính diện tích của các hình cơ bản như tam giác, hình vuông, hình chữ nhật, hình tròn. Ví dụ:
Diện tích tam giác = (1/2) * đáy * chiều cao
Ngoài bộ đề thi này, học sinh có thể tham khảo thêm các tài liệu ôn thi khác như:
Đề thi vào 10 môn Toán Hải Dương năm 2019 là một tài liệu ôn thi quan trọng giúp học sinh chuẩn bị tốt nhất cho kỳ thi sắp tới. Hy vọng rằng với những phân tích và hướng dẫn giải chi tiết trên, các em học sinh sẽ tự tin hơn và đạt được kết quả cao nhất trong kỳ thi tuyển sinh vào lớp 10.