Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp các đề thi thử vào lớp 10 môn Toán chất lượng cao. Đề số 23 là một trong những đề thi được thiết kế để giúp các em học sinh làm quen với cấu trúc đề thi, rèn luyện kỹ năng giải toán và tự tin hơn trong kỳ thi sắp tới.
Đề thi này bao gồm các dạng bài tập đa dạng, từ trắc nghiệm đến tự luận, bao phủ đầy đủ các kiến thức trọng tâm của chương trình Toán lớp 9.
Đề thi vào lớp 10 môn Toán - Đề số 23 có đáp án và lời giải chi tiết
Đề bài
Câu I (2,0 điểm)
1. Tính giá trị của biểu thức \(A = \sqrt 5 \left( {\sqrt {20} - \sqrt 5 } \right) + 1\)
2. Tìm tham số m để đường thẳng \(y = \left( {m - 1} \right)x + 2018\) có hệ số góc bằng 3.
Câu II (3,0 điểm)
1. Giải hệ phương trình \(\left\{ \begin{array}{l}x + 4y = 8\\2x + 5y = 13\end{array} \right.\)
2. Cho biểu thức \(B = \left( {\dfrac{6}{{a - 1}} + \dfrac{{10 - 2\sqrt a }}{{a\sqrt a - a - \sqrt a + 1}}} \right).\dfrac{{{{\left( {\sqrt a - 1} \right)}^2}}}{{4\sqrt a }}\) (với \(a > 0,\,a \ne 1\))
a) Rút gọn biểu thức B.
b) Đặt \(C = B.\left( {a - \sqrt a + 1} \right)\). So sánh C và 1.
3. Cho phương trình \({x^2} - \left( {m + 2} \right)x + 3m - 3 = 0\,\,\left( 1 \right)\), với x là ẩn, m là tham số.
a) Giải phương trình (1) khi \(m = - 1.\)
b) Tìm các giá trị của m để phương trình (1) có hai nghiệm phân biệt \({x_1};\,\,{x_2}\) sao cho \({x_1};\,\,{x_2}\) là độ dài hai cạnh góc vuông của một tam giác vuông có độ dài cạnh huyền bằng 5.
Câu III (1,5 điểm)
Bạn Linh đi xe đạp từ nhà đến trường với quãng đường 10 km. Khi đi từ trường về nhà, vẫn trên cung đường ấy, do lượng xe tham gia giao thông nhiều hơn nên bạn Linh phải giảm vận tốc 2 km/h so với khi đến trường. Vì vậy thời gian về nhà nhiều hơn thời gian đến trường là 15 phút. Tính vận tốc của xe đạp khi bạn Linh đi từ nhà đến trường.
Câu IV (3,0 điểm)
Cho tam giác \(ABC\) nhọn. Đường tròn tâm O đường kính BC cắt các cạnh \(AB,AC\) lần lượt tại các điểm \(M,N\,\,\left( {M \ne B,N \ne C} \right)\). Gọi H là giao điểm của BN và CM; P là giao điểm của AH và BC.
1. Chứng minh tứ giác AMHN nội tiếp được trong một đường tròn.
2. Chứng minh \(BM.BA = BP.BC\).
3. Trong trường hợp đặc biệt khi tam giác \(ABC\) đều cạnh bằng \(2a\) . Tính chu vi đường tròn ngoại tiếp tứ giác AMHN.
4. Từ điểm A kẻ các tiếp tuyến AE và AF của đường tròn tâm O đường kính BC (E, F là các tiếp điểm). Chứng minh ba điểm \(E,H,F\) thẳng hàng.
Câu V (0,5 điểm)
Tìm giá trị nhỏ nhất của biểu thức \(\) với \(x > 0\)
Lời giải chi tiết
Câu I.
1. Tính giá trị của biểu thức \(A = \sqrt 5 \left( {\sqrt {20} - \sqrt 5 } \right) + 1\)
\(\begin{array}{l}A = \sqrt 5 \left( {\sqrt {20} - \sqrt 5 } \right) + 1\\A = \sqrt 5 \left( {\sqrt {{2^2}.5} - \sqrt 5 } \right) + 1\\A = \sqrt 5 \left( {2\sqrt 5 - \sqrt 5 } \right) + 1\\A = \sqrt 5 .\sqrt 5 + 1\\A = 5 + 1\\A = 6\end{array}\)
2. Tìm tham số m để đường thẳng \(y = \left( {m - 1} \right)x + 2018\) có hệ số góc bằng 3.
Đường thẳng \(y = \left( {m - 1} \right)x + 2018\) có hệ số góc bằng 3 \( \Leftrightarrow m - 1 = 3 \Leftrightarrow m = 4\).
Câu II.
1. Giải hệ phương trình \(\left\{ \begin{array}{l}x + 4y = 8\\2x + 5y = 13\end{array} \right.\)
\(\left\{ \begin{array}{l}x + 4y = 8\\2x + 5y = 13\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2x + 8y = 16\\2x + 5y = 13\end{array} \right. \)
\(\Leftrightarrow \left\{ \begin{array}{l}3y = 3\\x = 8 - 4y\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 1\\x = 4\end{array} \right.\).
Vậy nghiệm của hệ phương trình là \(\left( {x;y} \right) = \left( {4;1} \right)\).
2. Cho biểu thức \(B = \left( {\dfrac{6}{{a - 1}} + \dfrac{{10 - 2\sqrt a }}{{a\sqrt a - a - \sqrt a + 1}}} \right).\dfrac{{{{\left( {\sqrt a - 1} \right)}^2}}}{{4\sqrt a }}\) (với \(a > 0,\,a \ne 1\))
a) Rút gọn biểu thức B.
Với \(a > 0,\,a \ne 1\) ta có:
\(\begin{array}{l}B = \left( {\dfrac{6}{{a - 1}} + \dfrac{{10 - 2\sqrt a }}{{a\sqrt a - a - \sqrt a + 1}}} \right).\dfrac{{{{\left( {\sqrt a - 1} \right)}^2}}}{{4\sqrt a }}\\B = \left( {\dfrac{6}{{a - 1}} + \dfrac{{10 - 2\sqrt a }}{{a\left( {\sqrt a - 1} \right) - \left( {\sqrt a - 1} \right)}}} \right).\dfrac{{{{\left( {\sqrt a - 1} \right)}^2}}}{{4\sqrt a }}\\B = \left( {\dfrac{6}{{a - 1}} + \dfrac{{10 - 2\sqrt a }}{{\left( {\sqrt a - 1} \right)\left( {a - 1} \right)}}} \right).\dfrac{{{{\left( {\sqrt a - 1} \right)}^2}}}{{4\sqrt a }}\\B = \dfrac{{6\left( {\sqrt a - 1} \right) + 10 - 2\sqrt a }}{{\left( {\sqrt a - 1} \right)\left( {a - 1} \right)}}.\dfrac{{{{\left( {\sqrt a - 1} \right)}^2}}}{{4\sqrt a }}\\B = \dfrac{{6\sqrt a - 6 + 10 - 2\sqrt a }}{{\left( {\sqrt a - 1} \right)\left( {a - 1} \right)}}.\dfrac{{{{\left( {\sqrt a - 1} \right)}^2}}}{{4\sqrt a }}\\B = \dfrac{{4\left( {\sqrt a + 1} \right)}}{{{{\left( {\sqrt a - 1} \right)}^2}\left( {\sqrt a + 1} \right)}}.\dfrac{{{{\left( {\sqrt a - 1} \right)}^2}}}{{4\sqrt a }}\\B = \dfrac{4}{{{{\left( {\sqrt a - 1} \right)}^2}}}.\dfrac{{{{\left( {\sqrt a - 1} \right)}^2}}}{{4\sqrt a }}\\B = \dfrac{1}{{\sqrt a }}\end{array}\)
b) Đặt \(C = B.\left( {a - \sqrt a + 1} \right)\). So sánh C và 1.
\(\begin{array}{l}B = \dfrac{1}{{\sqrt a }} \Rightarrow C = B.\left( {a - \sqrt a + 1} \right)\\ \Rightarrow C = \dfrac{1}{{\sqrt a }}\left( {a - \sqrt a + 1} \right) = \sqrt a - 1 + \dfrac{1}{{\sqrt a }}\end{array}\)
Áp dụng BĐT Cauchy ta có \(\sqrt a + \dfrac{1}{{\sqrt a }} \ge 2\sqrt {\sqrt a .\dfrac{1}{{\sqrt a }}} = 2 \)
\(\Rightarrow \sqrt a - 1 + \dfrac{1}{{\sqrt a }} \ge 2 - 1 = 1\)
Dấu bằng xảy ra \( \Leftrightarrow \sqrt a = \dfrac{1}{{\sqrt a }} \Leftrightarrow a = 1\).
Vậy \(C \ge 1\) và \(C = 1 \Leftrightarrow a = 1\).
3. Cho phương trình \({x^2} - \left( {m + 2} \right)x + 3m - 3 = 0\,\,\left( 1 \right)\), với x là ẩn, m là tham số.
a) Giải phương trình (1) khi \(m = - 1.\)
Thay \(m = - 1\) vào phương trình (1) ta có:
\(\begin{array}{l}\,\,\,\,\,\,{x^2} - x - 6 = 0\\ \Leftrightarrow {x^2} - 3x + 2x - 6 = 0\\ \Leftrightarrow x\left( {x - 3} \right) + 2\left( {x - 3} \right) = 0\\ \Leftrightarrow \left( {x - 3} \right)\left( {x + 2} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 3\\x = - 2\end{array} \right.\end{array}\)
Vậy khi \(m = - 1\) thì tập nghiệm của phương trình là \(S = \left\{ { - 2;3} \right\}\).
b) Tìm các giá trị của m để phương trình (1) có hai nghiệm phân biệt \({x_1};\,\,{x_2}\) sao cho \({x_1};\,\,{x_2}\) là độ dài hai cạnh góc vuông của một tam giác vuông có độ dài cạnh huyền bằng 5.
Hai nghiệm \({x_1};{x_2}\) là hai cạnh của một tam giác vuông nên \({x_1};{x_2} > 0\)
Để phương trình có hai nghiệm phân biệt dương \({x_1};\,\,{x_2}\)
\( \Leftrightarrow \left\{ \begin{array}{l}\Delta > 0\\S = {x_1} + {x_2} > 0\\P = {x_1}.{x_2} > 0\end{array} \right.\left( * \right)\)
Khi đó theo hệ thức Vi-ét ta có \(\left\{ \begin{array}{l}{x_1} + {x_2} = m + 2\\{x_1}{x_2} = 3m - 3\end{array} \right.\)
\(\left( * \right) \Leftrightarrow \left\{ \begin{array}{l}{\left( {m + 2} \right)^2} - 4\left( {3m - 3} \right) > 0\\m + 2 > 0\\3m - 3 > 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}{\left( {m - 4} \right)^2} > 0\\m + 2 > 0\\3m - 3 > 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}m \ne 4\\m > - 2\\m > 1\end{array} \right. \Leftrightarrow m > 1;m \ne 4\)
Vì \({x_1};\,\,{x_2}\) là độ dài hai cạnh góc vuông của một tam giác vuông có độ dài cạnh huyền bằng 5 nên áp dụng định lí Pi-ta-go ta có:
\(\begin{array}{l}\,\,\,\,\,\,x_1^2 + x_2^2 = {5^2} = 25\\ \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2} = 25\\ \Leftrightarrow {\left( {m + 2} \right)^2} - 2\left( {3m - 3} \right) = 25\\ \Leftrightarrow {m^2} + 4m + 4 - 6m + 6 = 25\\ \Leftrightarrow {m^2} - 2m - 15 = 0\\ \Leftrightarrow {m^2} - 5m + 3m - 15 = 0\\ \Leftrightarrow m\left( {m - 5} \right) + 3\left( {m - 5} \right) = 0\\ \Leftrightarrow \left( {m - 5} \right)\left( {m + 3} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}m = 5\left( {tm} \right)\\m = - 3\left( {ktm} \right)\end{array} \right.\,\,\end{array}\)
Vậy \(m = 5\) thỏa mãn điều kiện bài toán.
Câu III.
Bạn Linh đi xe đạp từ nhà đến trường với quãng đường 10 km. Khi đi từ trường về nhà, vẫn trên cung đường ấy, do lượng xe tham gia giao thông nhiều hơn nên bạn Linh phải giảm vận tốc 2 km/h so với khi đến trường. Vì vậy thời gian về nhà nhiều hơn thời gian đến trường là 15 phút. Tính vận tốc của xe đạp khi bạn Linh đi từ nhà đến trường.
Gọi vận tốc của xe đạp khi bạn Linh đi từ nhà đến trường là \(x\,\,\left( {km/h} \right)\) (ĐK: \(x > 2\))
Khi đó vận tốc của xe đạp khi bạn Linh đi từ trường về nhà là \(x - 2\,\,\left( {km/h} \right)\).
Thời gian bạn Linh đi từ nhà đến trường là \(\dfrac{{10}}{x}\,\,\left( h \right)\)
Thời gian bạn Linh đi từ trường về nhà là \(\dfrac{{10}}{{x - 2}}\,\,\left( h \right)\)
Do thời gian về nhà nhiều hơn thời gian đến trường là 15 phút \( = \dfrac{{15}}{{60}} = \dfrac{1}{4}\,\left( h \right)\) nên ta có phương trình:
\(\begin{array}{l}\,\,\,\,\,\dfrac{{10}}{{x - 2}} - \dfrac{{10}}{x} = \dfrac{1}{4}\\ \Leftrightarrow 40x - 40\left( {x - 2} \right) = x\left( {x - 2} \right)\\ \Leftrightarrow 40x - 40x + 80 = {x^2} - 2x\\ \Leftrightarrow {x^2} - 2x - 80 = 0\\ \Leftrightarrow {x^2} - 10x + 8x - 80 = 0\\ \Leftrightarrow x\left( {x - 10} \right) + 8\left( {x - 10} \right) = 0\\ \Leftrightarrow \left( {x - 10} \right)\left( {x + 8} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 10\,\,\,\left( {tm} \right)\\x = - 8\,\,\left( {ktm} \right)\end{array} \right.\end{array}\)
Vậy vận tốc của xe đạp khi bạn Linh đi từ nhà đến trường là 10 km/h.
Câu IV.
Cho tam giác \(ABC\) nhọn. Đường tròn tâm O đường kính BC cắt các cạnh \(AB,AC\) lần lượt tại các điểm \(M,N\,\,\left( {M \ne B,N \ne C} \right)\). Gọi H là giao điểm của BN và CM; P là giao điểm của AH và BC.
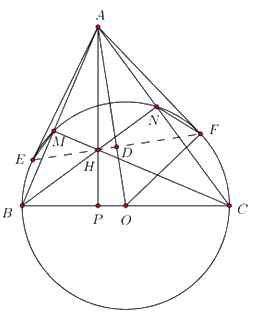
1. Chứng minh tứ giác AMHN nội tiếp được trong một đường tròn.
Ta có \(\widehat {BMC} = \widehat {BNC} = {90^0}\) (góc nội tiếp chắn nửa đường tròn)
\( \Rightarrow \widehat {AMH} = \widehat {ANH} = {90^0}\)
\(\) Tứ giác \(AMHN\) có \(\widehat {AMH} + \widehat {ANH} = {90^0} + {90^0} = {180^0}\) \( \Rightarrow \) Tứ giác AMHN là tứ giác nội tiếp đường tròn đường kính AH (Tứ giác có tổng hai góc đối bằng 1800).
2. Chứng minh \(BM.BA = BP.BC\).
Xét \(\Delta ABP\) và \(\Delta CBM\) có:
\(\widehat {APB} = \widehat {CMB} = {90^0}\) ;
\(\widehat {ABC}\) chung;
\( \Rightarrow \Delta ABP \sim \Delta CBM\,\,\left( {g.g} \right)\)
\(\Rightarrow \dfrac{{BA}}{{BP}} = \dfrac{{BC}}{{BM}}\)
\(\Rightarrow BM.BA = BP.BC\)
3. Trong trường hợp đặc biệt khi tam giác \(ABC\) đều cạnh bằng \(2a\) . Tính chu vi đường tròn ngoại tiếp tứ giác AMHN.
Ta có \(BN \bot AC;\,\,CM \bot AB;\,\,BN \cap CM = H \Rightarrow H\) là trực tâm tam giác ABC.
\(\Delta ABC\) đều \( \Rightarrow \widehat {ABP} = \widehat {ABC} = {60^0}\)
Xét tam giác vuông ABP có \(AP = AB.\sin {60^0} = 2a.\dfrac{{\sqrt 3 }}{2} = a\sqrt 3 \)
Do H là trực tâm tam giác ABC nên đồng thời H cũng là trọng tâm của tam giác ABC\( \Rightarrow AH = \dfrac{2}{3}AP = \dfrac{2}{3}a\sqrt 3 = \dfrac{{2a\sqrt 3 }}{3}\)
Vì AH là đường kính của đường tròn ngoại tiếp tứ giác AMHN nên bán kính của đường tròn ngoại tiếp tứ giác AMHN là \(\dfrac{{AH}}{2} = \dfrac{{a\sqrt 3 }}{3}\).
Vậy chu vi đường tròn ngoại tiếp tứ giác AMHN là \(C = 2\pi .\dfrac{{a\sqrt 3 }}{3} = \dfrac{{2\pi a\sqrt 3 }}{3}\).
4. Từ điểm A kẻ các tiếp tuyến AE và AF của đường tròn tâm O đường kính BC (E, F là các tiếp điểm). Chứng minh ba điểm \(E,H,F\) thẳng hàng.
Gọi D là giao điểm của OA và EF.
H là trực tâm tam giác ABC \( \Rightarrow AH \bot BC \)
\(\Rightarrow AP \bot BC\) \( \Rightarrow \widehat {APC} = {90^0}\)
\(\widehat {BNC} = {90^0}\) (góc nội tiếp chắn nửa đường tròn) \( \Rightarrow \widehat {ANH} = {90^0}\)
Xét \(\Delta AHN\) và \(\Delta ACP\) có :
\(\widehat {ANH} = \widehat {APC} = {90^0}\) (cmt)
\(\widehat {PAC}\) chung ;
\( \Rightarrow \Delta AHN \sim \Delta ACP\,\left( {g.g} \right)\)
\(\Rightarrow \dfrac{{AH}}{{AC}} = \dfrac{{AN}}{{AP}}\)
\(\Rightarrow AH.AP = AN.AC\,\,\,\left( 1 \right)\)
Xét \(\Delta AFN\) và \(\Delta ACF\) có :
\(\widehat {FAC}\) chung ;
\(\widehat {AFN} = \widehat {ACF}\) (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung NF).
\( \Rightarrow \Delta AFN \sim \Delta ACF\,\,\left( {g.g} \right)\)
\(\Rightarrow \dfrac{{AF}}{{AC}} = \dfrac{{AN}}{{AF}}\)
\(\Rightarrow AN.AC = A{F^2}\,\,\,\left( 2 \right)\)
Ta có \(AF \bot OF\,\,\left( {gt} \right) \Rightarrow \Delta OAF\) vuông tại F.
Có \(AE = AF\,\) (tính chất hai tiếp tuyến cắt nhau) ; \(OE = OF\,\,\left( { = R} \right)\) \( \Rightarrow OA\) là trung trực của EF.
\( \Rightarrow OA \bot EF \Rightarrow FD\)là đường cao của tam giác vuông OAF.
\( \Rightarrow A{F^2} = AD.AO\,\,\,\left( 3 \right)\)(hệ thức lượng trong tam giác vuông).
Từ (1), (2) và (3) \( \Rightarrow AH.AP = AD.AO \)
\(\Rightarrow \dfrac{{AH}}{{AO}} = \dfrac{{AD}}{{AP}}\)
Xét \(\Delta AHD\) và \(\Delta AOP\) có:
\(\widehat {OAP}\) chung;
\(\dfrac{{AH}}{{AO}} = \dfrac{{AD}}{{AP}}\,\,\left( {cmt} \right)\);
\( \Rightarrow \Delta AHD \sim \Delta AOP\,\,\left( {c.g.c} \right)\).
\( \Rightarrow \widehat {ADH} = \widehat {APO} = {90^0}\) \( \Rightarrow HD \bot OA\)
Từ đó ta có qua điểm D ta kẻ được \(EF \bot OA\) (cmt) và \(\).
Vậy ba điểm \(E,H,F\) thẳng hàng.
Câu V.
Tìm giá trị nhỏ nhất của biểu thức \(P = \dfrac{{81{x^2} + 18225x + 1}}{{9x}} - \dfrac{{6\sqrt x + 8}}{{x + 1}}\) với \(x > 0\)
Ta có:
\(\begin{array}{l}P = \dfrac{{81{x^2} + 18225x + 1}}{{9x}} - \dfrac{{6\sqrt x + 8}}{{x + 1}}\\P = 9x + 2025 + \dfrac{1}{{9x}} - \dfrac{{6\sqrt x + 8}}{{x + 1}}\end{array}\)
Ta chứng minh \(\dfrac{{6\sqrt x + 8}}{{x + 1}} \le 9\,\,\forall x > 0\).
Giả sử :
\(\begin{array}{l}\,\,\,\,\,\,\dfrac{{6\sqrt x + 8}}{{x + 1}} \le 9\\ \Leftrightarrow \dfrac{{6\sqrt x + 8}}{{x + 1}} - \dfrac{{9x + 9}}{{x + 1}} \le 0\\ \Leftrightarrow \dfrac{{6\sqrt x + 8 - 9x - 9}}{{x + 1}} \le 0\\ \Leftrightarrow \dfrac{{ - 9x + 6\sqrt x - 1}}{{x + 1}} \le 0\\ \Leftrightarrow \dfrac{{ - {{\left( {3\sqrt x - 1} \right)}^2}}}{{x + 1}} \le 0\end{array}\)
Ta có \(x > 0 \Leftrightarrow x + 1 > 1;\,\,{\left( {3\sqrt x - 1} \right)^2} \ge 0 \)
\(\Rightarrow \dfrac{{ - {{\left( {3\sqrt x - 1} \right)}^2}}}{{x + 1}} \le 0\,\,\forall x > 0\)
\( \Rightarrow \dfrac{{6\sqrt x + 8}}{{x + 1}} \le 9\,\,\forall x > 0 \)
\(\Rightarrow - \dfrac{{6\sqrt x + 8}}{{x + 1}} \ge - 9\forall x > 0\)
\(\begin{array}{l} \Rightarrow P \ge 2\sqrt {9x.\dfrac{1}{{9x}}} + 2025 - 9\\ \Leftrightarrow P \ge 2018\end{array}\)
Dấu bằng xảy ra \( \Leftrightarrow \left\{ \begin{array}{l}9x = \dfrac{1}{{9x}}\\3\sqrt x - 1 = 0\end{array} \right.\)
\(\Leftrightarrow \left\{ \begin{array}{l}81{x^2} = 1\\\sqrt x = \dfrac{1}{3}\end{array} \right. \Leftrightarrow x = \dfrac{1}{9}\)
Vậy \({P_{\min }} = 2018 \Leftrightarrow x = \dfrac{1}{9}\).
Đề thi vào lớp 10 môn Toán là một bước ngoặt quan trọng trong quá trình học tập của các em học sinh. Để đạt kết quả tốt nhất, việc luyện tập thường xuyên với các đề thi thử là vô cùng cần thiết. Đề số 23 mà giaitoan.edu.vn cung cấp được xây dựng dựa trên cấu trúc đề thi chính thức của các trường THPT chuyên và các tỉnh thành trên cả nước.
Đề thi Đề số 23 bao gồm các phần chính sau:
Dưới đây là một số câu hỏi tiêu biểu trong đề thi Đề số 23:
Cho phương trình 2x + 3 = 7. Nghiệm của phương trình là:
(Hướng dẫn giải: Giải phương trình 2x + 3 = 7, ta được 2x = 4, suy ra x = 2. Vậy đáp án đúng là B.)
Giải hệ phương trình sau:
{ x + y = 5 2x - y = 1 }
(Hướng dẫn giải: Cộng hai phương trình, ta được 3x = 6, suy ra x = 2. Thay x = 2 vào phương trình x + y = 5, ta được y = 3. Vậy nghiệm của hệ phương trình là (x, y) = (2, 3).)
Cho tam giác ABC vuông tại A, có AB = 3cm, AC = 4cm. Tính độ dài cạnh BC.
(Hướng dẫn giải: Áp dụng định lý Pitago trong tam giác vuông ABC, ta có BC2 = AB2 + AC2 = 32 + 42 = 25. Suy ra BC = 5cm.)
Để đạt kết quả tốt nhất trong kỳ thi vào lớp 10 môn Toán, các em học sinh cần lưu ý những điều sau:
giaitoan.edu.vn cung cấp:
Hãy luyện thi ngay hôm nay với Đề số 23 và các đề thi khác tại giaitoan.edu.vn để đạt kết quả tốt nhất trong kỳ thi vào lớp 10 môn Toán!
| Dạng bài | Ví dụ |
|---|---|
| Phương trình bậc nhất một ẩn | Giải phương trình: 3x - 5 = 10 |
| Hệ phương trình bậc nhất hai ẩn | Giải hệ phương trình: x + y = 7, x - y = 1 |
| Hình học phẳng | Tính diện tích tam giác khi biết độ dài các cạnh |