Chào mừng bạn đến với bài viết cung cấp Đề số 14 - Đề thi vào lớp 10 môn Toán. Đây là một trong những đề thi thử quan trọng giúp học sinh làm quen với cấu trúc đề thi và rèn luyện kỹ năng giải toán.
Giaitoan.edu.vn cung cấp đề thi chính thức, đáp án chi tiết và lời giải bài bản, giúp bạn tự tin bước vào kỳ thi tuyển sinh lớp 10.
Đề thi vào lớp 10 môn Toán - Đề số 14 có đáp án và lời giải chi tiết
Đề bài
I. PHẦN TRẮC NGHIỆM:
Câu 1: Tam giác MNP đều, nội tiếp đường tròn (O; R), khi đó số đo \(\widehat {NOP}\) là:
A. \({150^0}\)
B. \({60^0}\)
C. \({30^0}\)
D. \({120^0}\)
Câu 2: Phương trình nào sau đây có hai nghiệm trái dấu?
A. \({x^2} - 2017x - 2018 = 0\)
B. \({x^2} - 2018x + 2017 = 0\)
C. \( - {x^2} + 2017x - 2018 = 0\)
D. \({x^2} - 2019x + 2018 = 0\)
Câu 3: Tìm m để hàm số \(y = \dfrac{3}{{m + 2}}x + 1\) đồng biến trên tập số thực \(R.\)
A. \(m > - 2\)
B. \(m < - 2\)
C. \(m > 2\)
D. \(m \le - 2\)
Câu 4: Biết \(\left( {a;\;b} \right)\) là nghiệm của hệ phương trình \(\left\{ \begin{array}{l}4x - 3y = 2\\x + y = 4\end{array} \right..\) Khi đó giá trị của biểu thức \(2{a^2} - {b^2}\) là:
A. 4 B. -12
C. -4 D. 8
Câu 5: Giá trị của biểu thức \(\sin {62^0} - \cos {28^0}\) bằng:
A. 0
B. 1
C. \(2\sin {62^0}\)
D. \(2\cos {28^0}\)
Câu 6: Hệ số góc của đường thẳng \(y = - 5x + 7\) là:
A. \( - 5x\)
B. \(5\)
C. \( - 5\)
D. \(7\)
Câu 7: Cho tam giác \(ABC\) vuông tại \(C.\) Biết \(\sin B = \dfrac{1}{3},\) khi đó \(\tan A\) bằng:
A. \(\dfrac{{2\sqrt 2 }}{3}\)
B. \(3\)
C. \(2\sqrt 2 \)
D. \(\dfrac{1}{{2\sqrt 2 }}\)
Câu 8: Cho hai đường tròn \(\left( {O;\;4cm} \right)\) và đường tròn \(\left( {I;\;2cm} \right),\) biết \(OI = 6cm.\) Số tiếp tuyến chung của hai đường tròn đó là:
A. 4 B. 3
C. 2 D. 1
Câu 9: Kết quả của phép tính \(\sqrt {{{\left( {2 - \sqrt 5 } \right)}^2}} - \sqrt 5 \) là:
A. \(2\sqrt 5 - 2\)
B. \( - 2\)
C. \(2\)
D. \(2 - 2\sqrt 5 \)
Câu 10: Tìm m để hai đường thẳng \(\left( d \right):\;\;y = 3x + 1\) và \(\left( {d'} \right):\;\;y = \left( {m - 1} \right)x - 2m\) song song với nhau.
A. \(m = - \dfrac{1}{2}\)
B. \(m = 4\)
C. \(m = - \dfrac{3}{2}\)
D. \(m \ne 4\)
Câu 11: Từ một miếng tôn có hình dạng là nửa hình tròn bán kính 1m, người ta cắt ra một hình chữ nhật (phần tô đậm như hình vẽ). Phần hình chữ nhật có diện tích lớn nhất có thể cắt được là:
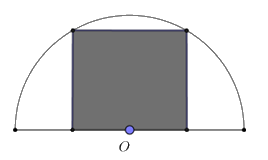
A. \(1,6{m^2}\)
B. \(0,5{m^2}\)
C. \(1{m^2}\)
D. \(2{m^2}\)
Câu 12: Cho tứ giác \(ABCD\) nội tiếp đường tròn \(\left( O \right)\) đường kính \(AC\), có \(\widehat {BAC} = {60^0}\) (hình vẽ). Khi đó số đo của \(\widehat {ADB}\) là:
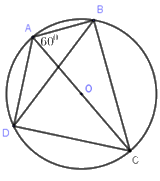
A. \({45^0}\) B. \({60^0}\)
C. \({40^0}\) D. \({30^0}\).
Câu 13: Một hình cầu có đường kính 6cm. Diện tích mặt cầu đó là:
A. \(36\pi c{m^2}\)
B. \(12\pi c{m^2}\)
C. \(216\pi c{m^2}\)
D. \(72\pi c{m^2}\)
Câu 14: Cặp số nào sau đây là một nghiệm của phương trình \(x - 3y = - 1?\)
A. \(\left( {2;\;0} \right)\)
B. \(\left( {2;\;1} \right)\)
C. \(\left( {1;\;2} \right)\)
D. \(\left( {2;\; - 1} \right)\)
Câu 15: Trên cùng mặt phẳng tọa độ Oxy cho ba đường thẳng \(y = x + 2;\;y = 2x + 1\) và \(y = \left( {{m^2} - 1} \right)x - 2m + 1.\) Tìm giá trị của m để ba đường thẳng cùng đi qua một điểm.
A. \(m = - 3\)
B. \(m \in \left\{ { - 3;\;1} \right\}\)
C. \(m \in \left\{ { - 1;\;3} \right\}\)
D. \(m = 1\)
Câu 16: Trong mặt phẳng tọa độ Oxy, tập nghiệm của phương trình \(4x + y = 1\) được biểu diễn bởi đồ thị hàm số nào dưới đây?
A. \(y = 4x + 1\)
B. \(y = - 4x - 1\)
C. \(y = - 4x + 1\)
D. \(y = 4x - 1\)
Câu 17: Cho \(\Delta ABC\) vuông tại \(A,\) đường cao \(AH.\) Biết \(BH = 3,2cm;\;\;BC = 5cm\) thì độ dài \(AB\) bằng:
A. \(8cm\) B. -\(16cm\)
C. \(1,8cm\) D. \(4cm\)
Câu 18: Biết phương trình \(3{x^2} + 6x - 9 = 0\) có hai nghiệm \({x_1};{x_2}\). Giả sử \({x_1} < {x_2}\) khi đó biểu thức \(\dfrac{{{x_2}}}{{{x_1}}}\) có giá trị là:
A. \(\dfrac{1}{3}\)
B. \( - \dfrac{1}{3}\)
C. \( - 3\)
D. 3
Câu 19: Cho các đường tròn \(\left( {A;3cm} \right);\,\,\left( {B;\;5cm} \right);\,\,\left( {C;2cm} \right)\) đôi một tiếp xúc ngoài với nhau. Chu vi của \(\Delta ABC\) là:
A. 20cm
B. \(10\sqrt 2 cm\)
C. 10cm
D. \(10\sqrt 3 cm\)
Câu 20: Điều kiện xác định của biểu thức \(\sqrt {x - 15} \) là:
A. \(x \le - 15\)
B. \(x \ge 15\)
C. \(x \ge - 15\)
D. \(x \le 15\)
Câu 21: Kết quả rút gọn biểu thức \(\dfrac{1}{{\sqrt {13} + \sqrt {15} }} + \dfrac{1}{{\sqrt {15} + \sqrt {17} }}\) là:
A. \(\dfrac{{\sqrt {13} - \sqrt {17} }}{2}\)
B. \(\dfrac{{\sqrt {17} + \sqrt {13} }}{2}\)
C. \(\sqrt {17} - \sqrt {13} \)
D. \(\dfrac{{\sqrt {17} - \sqrt {13} }}{2}\)
Câu 22: Đổ nước vào một chiếc thùng hình trụ có bán kính 20cm. Nghiêng thùng sao cho mặt nước chạm miệng thùng và đáy thùng (như hình vẽ) thì mặt nước tạo với đáy thùng một góc 450. Thể tích của thùng là:
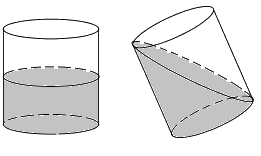
A. \(400\pi \,\,\left( {c{m^3}} \right)\)
B. \(32000\pi \,\left( {c{m^3}} \right)\)
C. \(16000\pi \,\left( {c{m^3}} \right)\)
D. \(8000\pi \,\left( {c{m^3}} \right)\)
Câu 23: Cho hai đường thẳng \(\left( {{d_1}} \right):\,\,y = - 2x + 3\) và \(\left( {{d_2}} \right):\,\,y = - \dfrac{1}{2}x + 3\). Khẳng định nào sau đây là đúng?
A. (d1) và (d2) trùng nhau
B. (d1) và (d2) cắt nhau tại một điểm trên trục trung
C. (d1) và (d2) song song với nhau
D. (d1) và (d2) cắt nhau tại một điểm trên trục hoành.
Câu 24: Số nhà của bạn Nam là một số tự nhiên có hai chữ số. Nếu thêm chữ số 7 vào bên trái số đó thì được một số kí hiệu là A. Nếu thêm chữ số 7 vào bên phải chữ số đó thì được một số kí hiệu là B. Tìm số nhà của bạn Nam biết \(A - B = 252\).
A. 45 B. 54
C. 90 D. 49
Câu 25: Trong mặt phẳng tọa độ Oxy, cho đường thẳng \(\left( d \right):\,\,y = x - m + 2\) và parabol: \(\left( P \right):\,\,y = {x^2}\). Tìm m để (d) và (P) cắt nhau tại hai điểm phân biệt nằm trên cùng một nửa mặt phẳng có bờ là trục tung:
B. \(\dfrac{4}{9} < m < 2\)
C. \(2 < m < \dfrac{9}{4}\)
D. \(m < \dfrac{4}{9}\)
II. PHẦN TỰ LUẬN: 45 PHÚT
Câu 1 (1,5 điểm).
a) Rút gọn biểu thức \(P = \sqrt 3 \left( {\sqrt {12} - 3} \right) + \sqrt {27} \)
b) Tìm giá trị của m để đồ thị hàm số \(y = m{x^2}\) đi qua điểm \(A\left( {2;4} \right)\).
c) Giải phương trình \({x^2} - 6x + 5 = 0\)
Câu 2 (1,5 điểm). Cho hệ phương trình \(\left\{ \begin{array}{l}3x - y = 2m + 3\\x + 2y = 3m + 1\end{array} \right.\) (m là tham số)
a) Giải hệ phương trình khi \(m = 2\).
b) Tìm m để hệ phương trình có nghiệm \(\left( {x;y} \right)\) thỏa mãn điều kiện \({x^2} + {y^2} = 5\).
Câu 3 (1,5 điểm) Cho đường tròn (O) đường kính AB và một dây CD vuông góc với AB tại H (H không trừng với các điểm A, B, O). Gọi M là trung điểm của AD. Chứng minh:
a) Bốn điểm O, M, D, H cùng thuộc một đường tròn.
b) MH vuông góc với BC.
Câu 4 (0,5 điểm) Cho x, y, z là 3 số thực dương thỏa mãn \({x^2} + {y^2} + {z^2} = 2\). Tìm giá trị lớn nhất của biểu thức
\(A = \dfrac{2}{{{x^2} + {y^2}}} + \dfrac{2}{{{y^2} + {z^2}}} + \dfrac{2}{{{z^2} + {x^2}}}\)\(\, - \dfrac{{{x^3} + {y^3} + {z^3}}}{{2xyz}}\)
Lời giải chi tiết
I. PHẦN TRẮC NGHIỆM:
1.D | 6.C | 11.C | 16.C | 21.D |
2.A | 7.C | 12.D | 17.D | 22.C |
3.A | 8.B | 13.A | 18.B | 23.B |
4.A | 9.B | 14.B | 19.A | 24.D |
5.A | 10.B | 15.C | 20.B | 25.C |
Câu 1:
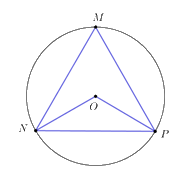
Tam giác \(MNP\) là tam giác đều \( \Rightarrow \widehat M = \widehat N = \widehat P = {60^0}.\)
Xét đường tròn \(\left( {O;\;R} \right)\) ta có: \(\widehat {NMP}\) là góc nội tiếp chắn cung \(NP.\)
\(\widehat {NOP}\) là góc ở tâm chắn cung \(NP.\)
\( \Rightarrow \widehat {NOP} = 2.\widehat {NMP} = {2.60^0} = {120^0}.\)
Chọn D.
Câu 2:
+) Phương trình \({x^2} - 2017x - 2018 = 0\) có \(ac = 1.\left( { - 2018} \right) = - 2018 < 0 \)
\(\Rightarrow \) phương trình có hai nghiệm trái dấu.
Chọn A.
Câu 3:
Hàm số đồng biến trên \(R \Leftrightarrow \dfrac{3}{{m + 2}} > 0\)
\(\Leftrightarrow m + 2 > 0\;\;\left( {do\;\;3 > 0} \right) \)
\(\Leftrightarrow m > - 2.\)
Chọn A.
Câu 4:
Ta có: \(\left\{ \begin{array}{l}4x - 3y = 2\\x + y = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}4x - 3y = 2\\3x + 3y = 12\end{array} \right. \)
\(\Leftrightarrow \left\{ \begin{array}{l}7x = 14\\y = 4 - x\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 2\end{array} \right..\)
\( \Rightarrow \) Hệ phương trình có nghiệm \(\left( {x;\;y} \right) = \left( {a;\;b} \right) = \left( {2;\;2} \right)\) hay \(a = 2,\;\;b = 2.\)
\( \Rightarrow 2{a^2} - {b^2} = {2.2^2} - {2^2} = 4.\)
Chọn A.
Câu 5:
Ta có: \({28^0} = {90^0} - {62^0} \Rightarrow \cos {28^0} = \sin {62^0}.\)
\( \Rightarrow \sin {62^0} - \cos {28^0} = \sin {62^0} - \sin {62^0} = 0.\)
Chọn A.
Câu 6:
Hệ số góc của đường thẳng \(y = - 5x + 7\) là: \(a = - 5.\)
Chọn C.
Câu 7:
Xét tam giác \(ABC\) vuông tại \(C\) ta có:
\(\sin B = \dfrac{{AC}}{{AB}} = \dfrac{1}{3} \Rightarrow AB = 3AC.\)
Mà áp dụng định lý Pi-ta-go ta có: \(A{B^2} = A{C^2} + B{C^2}\)
\(\Leftrightarrow {\left( {3AC} \right)^2} = A{C^2} + B{C^2}\)
\( \Leftrightarrow 8A{C^2} = B{C^2} \)
\(\Leftrightarrow \dfrac{{B{C^2}}}{{A{C^2}}} = 8 \)
\(\Leftrightarrow \dfrac{{BC}}{{AC}} = 2\sqrt 2 = \tan A.\)
Chọn C.
Câu 8:
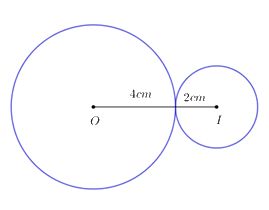
\( \Rightarrow \left( {O;\;4cm} \right)\) tiếp xúc ngoài với \(\left( {I;\;2cm} \right).\)Ta có: \(OI = 6cm = 4 + 2 = R + r.\)
\( \Rightarrow \)Hai đường tròn này có 3 đường tiếp tuyến chung.
Chọn B.
Câu 9:
\(\sqrt {{{\left( {2 - \sqrt 5 } \right)}^2}} - \sqrt 5 = \left| {2 - \sqrt 5 } \right| - \sqrt 5 \)\(\,= \sqrt 5 - 2 - \sqrt 5 = - 2.\)\(\;\;\;\left( {do\;\;2 - \sqrt 5 < 0} \right).\)
Chọn B.
Câu 10:
Ta có:\(d//d' \Leftrightarrow \left\{ \begin{array}{l}m - 1 = 3\\1 \ne - 2m\end{array} \right.\)
\(\Leftrightarrow \left\{ \begin{array}{l}m = 4\\m \ne - \dfrac{1}{2}\end{array} \right. \Leftrightarrow m = 4.\)
Chọn B.
Câu 11:
Gọi kích thước của miếng tôn như hình vẽ.
Áp dụng định lý Pi-ta-go ta có:
\({a^2} + {\left( {\dfrac{b}{2}} \right)^2} = 1 \Leftrightarrow {a^2} = \dfrac{{4 - {b^2}}}{4} \)
\(\Leftrightarrow a = \dfrac{{\sqrt {4 - {b^2}} }}{2}.\)
Khi đó diện tích miếng tôn hình chữ nhật là:
\(S = ab = \dfrac{{b\sqrt {4 - {b^2}} }}{2}.\)
Áp dụng bất đẳng thức Cô-si cho hai số ta có: \({b^2} + \sqrt {{{\left( {4 - {b^2}} \right)}^2}} \ge 2b\sqrt {4 - {b^2}} \)
\(\Leftrightarrow b\sqrt {4 - {b^2}} \le \dfrac{{{b^2} + 4 - {b^2}}}{2} = 2.\)
\( \Rightarrow S = \dfrac{{b\sqrt {4 - {b^2}} }}{2} \le \dfrac{2}{2} = 1.\)
Dấu “=” xảy ra \( \Leftrightarrow b = \sqrt {4 - {b^2}} \)
\(\Leftrightarrow {b^2} = 4 - {b^2} \Leftrightarrow {b^2} = 2 \Leftrightarrow b = \sqrt 2 .\)
Vậy diện tích lớn nhất có thể là \(1{m^2}.\)
Chọn C.
Câu 12:
Ta có: \(\widehat {ADC} = {90^0}\) (góc nội tiếp chắn nửa đường tròn).
\(\widehat {BDC} = \widehat {BAC} = {60^0}\) (góc nội tiếp cùng chắn cung \(BC\)).
Do đó \(\widehat {ADB} = \widehat {ADC} - \widehat {BDC} \)\(\,= {90^0} - {60^0} = {30^0}\).
Chọn D.
Câu 13:
Ta có diện tích mặt cầu đó là: \(S = 4\pi .{\left( {\dfrac{6}{2}} \right)^2} = 36\pi c{m^2}.\)
Chọn A.
Câu 14:
Thay \(\left( {2;\;0} \right)\) vào phương trình ta được: \(2 - 3.0 = 2 \ne - 1 \Rightarrow \left( {2;\;0} \right)\) không là nghiệm của phương trình.
Thay \(\left( {2;1} \right)\) vào phương trình ta được \(2 - 3.1 = 2 - 3 = - 1 \Rightarrow \left( {2;1} \right)\) là nghiệm của phương trình.
Chọn B.
Câu 15:
Tọa độ giao điểm của hai đường thẳng \(y = x + 2;\;y = 2x + 1\)là nghiệm của hệ phương trình:
\(\left\{ \begin{array}{l}y = x + 2\\y = 2x + 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = x + 2\\x + 2 = 2x + 1\end{array} \right. \)
\(\Leftrightarrow \left\{ \begin{array}{l}x = 1\\y = 3\end{array} \right. \Rightarrow A\left( {1;\;3} \right).\)
Để bai đường thẳng đã cho cùng đi qua một điểm thì đường thẳng \(y = \left( {{m^2} - 1} \right)x - 2m + 1\)phải đi qua điểm \(A\left( {1;\;\;3} \right).\) Khi đó ta có:
\(\begin{array}{l}3 = \left( {{m^2} - 1} \right).1 - 2m + 1\\ \Leftrightarrow {m^2} - 2m - 3 = 0\\ \Leftrightarrow \left( {m + 1} \right)\left( {m - 3} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}m + 1 = 0\\m - 3 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = - 1\\m = 3\end{array} \right..\end{array}\)
Vậy \(m \in \left\{ { - 1;\;\;3} \right\}.\)
Chọn C.
Câu 16:
Ta có: \(4x + y = 1 \Leftrightarrow y = 1 - 4x = - 4x + 1.\)
Chọn C.
Câu 17:
Áp dụng hệ thức lượng cho \(\Delta ABC\) vuông tại \(A\) có đường cao \(AH\) ta có:
\(A{B^2} = BH.BC\)
\(\Leftrightarrow A{B^2} = 3,2.5 = 16\)
\(\Leftrightarrow AB = 4cm.\)
Chọn D.
Câu 18.
Ta có \(a + b + c = 3 + 6 - 9 = 0 \Leftrightarrow \) Phương trình có hai nghiệm phân biệt \(\left[ \begin{array}{l}{x_2} = 1\\{x_1} = \dfrac{{ - 9}}{3} = - 3\end{array} \right.\) (do \({x_1} < {x_2}\))
\( \Rightarrow \dfrac{{{x_2}}}{{{x_1}}} = \dfrac{1}{{ - 3}} = - \dfrac{1}{3}\)
Chọn đáp án B.
Câu 19.
Do các đường tròn \(\left( {A;3cm} \right);\,\,\left( {B;\;5cm} \right);\,\,\left( {C;2cm} \right)\) đôi một tiếp xúc ngoài với nhau nên ta có:
\(\begin{array}{l}AB = 3 + 5 = 8\,\,\left( {cm} \right)\\AC = 3 + 2 = 5\,\,\left( {cm} \right)\\BC = 5 + 2 = 7\,\,\left( {cm} \right)\end{array}\)
Vậy chu vi tam giác ABC bằng \(8 + 5 + 7 = 20\,\,\left( {cm} \right)\).
Chọn đáp án A.
Câu 20.
\(\sqrt {x - 15} \) xác định \( \Leftrightarrow x - 15 \ge 0 \Leftrightarrow x \ge 15\).
Chọn đáp án B.
Câu 21.
\(\begin{array}{l}\,\,\,\,\,\dfrac{1}{{\sqrt {13} + \sqrt {15} }} + \dfrac{1}{{\sqrt {15} + \sqrt {17} }}\\ = \dfrac{{\sqrt {15} - \sqrt {13} }}{{\left( {\sqrt {15} - \sqrt {13} } \right)\left( {\sqrt {13} + \sqrt {15} } \right)}} + \dfrac{{\sqrt {17} - \sqrt {15} }}{{\left( {\sqrt {17} - \sqrt {15} } \right)\left( {\sqrt {15} + \sqrt {17} } \right)}}\\ = \dfrac{{\sqrt {15} - \sqrt {13} }}{{15 - 13}} + \dfrac{{\sqrt {17} - \sqrt {15} }}{{17 - 15}}\\ = \dfrac{{\sqrt {15} - \sqrt {13} }}{2} + \dfrac{{\sqrt {17} - \sqrt {15} }}{2}\\ = \dfrac{{\sqrt {15} - \sqrt {13} + \sqrt {17} - \sqrt {15} }}{2}\\ = \dfrac{{\sqrt {17} - \sqrt {13} }}{2}\end{array}\)
Chọn đáp án D.
Câu 22.
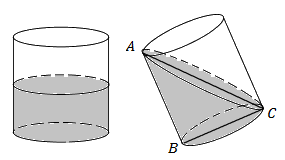
Đường kính đáy của chiếc thùng là 40cm \( \Rightarrow BC = 40cm\).
Vì mặt nước tạo với đáy thùng một góc 450 nên \(\widehat {ACB} = {45^0} \Rightarrow \Delta ABC\) vuông cân tại B.
\( \Rightarrow AB = BC = 40\,\,\left( {cm} \right) = h\)
Vậy thể tích của chiếc thùng là \(V = \pi {R^2}h = \pi {.20^2}.40 = 16000\pi \,\,\left( {c{m^3}} \right)\).
Chọn đáp án C.
Câu 23.
Xét phương trình hoành độ giao điểm \( - 2x + 3 = - \dfrac{1}{2}x + 3\)\(\, \Leftrightarrow - \dfrac{3}{2}x = 0 \Leftrightarrow x = 0\) \( \Rightarrow y = 3\).
Do đó hai đường thẳng (d1) và (d2) cắt nhau tại điểm \(\left( {0;3} \right)\) thuộc trục tung.
Chọn đáp án B.
Câu 24.
Gọi số nhà của bạn Nam là \(\overline {ab} \) \(\left( {a,b \in N;a \ne 0,\;0 \le a,b \le 9} \right)\)
Nếu thêm chữ số 7 vào bên trái số x ta được \(A = \overline {7ab} = 700 + \overline {ab} \)
Nếu thêm chữ số 7 vào bên trái số x ta được \(B = \overline {ab7} = \overline {ab} .10 + 7\)
\(A - B = 252\)
\(\Leftrightarrow 700 + \overline {ab} - \overline {ab} .10 + 7 = 252\)
\(\Leftrightarrow 9\overline {ab} = 441 \)
\(\Leftrightarrow \overline {ab} = 49\,\,\left( {tm} \right)\)
Vậy số nhà của bạn Nam là 49.
Chọn đáp án D.
Câu 25.
(d) và (P) cắt nhau tại hai điểm phân biệt nằm trên cùng một nửa mặt phẳng có bờ là trục tung khi và chỉ khi phương trình hoành độ giao điểm có hai nghiệm phân biệt cùng dấu.
Xét phương trình hoành độ giao điểm \({x^2} = x - m + 2 \)
\(\Leftrightarrow {x^2} - x + m - 2 = 0\,\,\left( * \right)\)
Để phương trình (*) có hai nghiệm cùng dấu
\( \Leftrightarrow \left\{ \begin{array}{l}\Delta = 1 - 4\left( {m - 2} \right) > 0\\P = m - 2 > 0\end{array} \right. \)
\(\Leftrightarrow \left\{ \begin{array}{l} - 4m + 9 > 0\\m > 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m < \dfrac{9}{4}\\m > 2\end{array} \right. \)
\(\Leftrightarrow 2 < m < \dfrac{9}{4}\)
Chọn đáp án C.
II. PHẦN TỰ LUẬN:
Câu 1.
a) Rút gọn biểu thức \(P = \sqrt 3 \left( {\sqrt {12} - 3} \right) + \sqrt {27} \)
\(\begin{array}{l}P = \sqrt 3 \left( {\sqrt {12} - 3} \right) + \sqrt {27} \\P = \sqrt 3 \left( {\sqrt {{2^2}.3} - 3} \right) + \sqrt {{3^2}.3} \\P = \sqrt 3 \left( {2\sqrt 3 - 3} \right) + 3\sqrt 3 \\P = 6 - 3\sqrt 3 + 3\sqrt 3 \\P = 6\end{array}\)
b) Tìm giá trị của m để đồ thị hàm số \(y = m{x^2}\) đi qua điểm \(A\left( {2;4} \right)\).
Thay tọa độ điểm \(A\left( {2;4} \right)\) vào hàm số ta có \(4 = m{.2^2} \Leftrightarrow 4 = m.4 \Leftrightarrow m = 1\)
Vậy \(m = 1\), khi đó đồ thị hàm số có dạng \(y = {x^2}\) và đi qua điểm \(A\left( {2;4} \right)\).
c) Giải phương trình \({x^2} - 6x + 5 = 0\)
\(\begin{array}{l}\,\,\,\,\,\,\,{x^2} - 6x + 5 = 0\\ \Leftrightarrow {x^2} - x - 5x + 5 = 0\\ \Leftrightarrow x\left( {x - 1} \right) - 5\left( {x - 1} \right) = 0\\ \Leftrightarrow \left( {x - 1} \right)\left( {x - 5} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = 5\end{array} \right.\end{array}\)
Vậy tập nghiệm của phương trình là \(S = \left\{ {1;5} \right\}\)
Câu 2.
a) Giải hệ phương trình khi \(m = 2\).
Thay \(m = 2\) vào hệ phương trình ta có:
\(\left\{ \begin{array}{l}3x - y = 7\\x + 2y = 7\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}6x - 2y = 14\\x + 2y = 7\end{array} \right.\)
\(\Leftrightarrow \left[ \begin{array}{l}7x = 21\\y = 3x - 7\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 3\\y = 2\end{array} \right.\)
Vậy nghiệm của hệ phương trình là \(\left( {x;y} \right) = \left( {3;2} \right)\).
b) Tìm m để hệ phương trình có nghiệm \(\left( {x;y} \right)\) thỏa mãn điều kiện \({x^2} + {y^2} = 5\).
\(\left\{ \begin{array}{l}3x - y = 2m + 3\\x + 2y = 3m + 1\end{array} \right. \)
\(\Leftrightarrow \left\{ \begin{array}{l}6x - 2y = 4m + 6\\x + 2y = 3m + 1\end{array} \right. \)
\(\Leftrightarrow \left\{ \begin{array}{l}7x = 7m + 7\\y = 3x - 2m - 3\end{array} \right.\)
\(\Leftrightarrow \left\{ \begin{array}{l}x = m + 1\\y = 3m + 3 - 2m - 3\end{array} \right.\)
\(\Leftrightarrow \left\{ \begin{array}{l}x = m + 1\\y = m\end{array} \right.\)
Do đó hệ phương trình có nghiệm \(\left( {x;y} \right) = \left( {m + 1;m} \right)\)
Khi đó ta có:
\(\begin{array}{l}{x^2} + {y^2} = 5 \Leftrightarrow {\left( {m + 1} \right)^2} + {m^2} = 5\\ \Leftrightarrow 2{m^2} + 2m + 1 = 5\\ \Leftrightarrow {m^2} + m - 2 = 0 \\\Leftrightarrow {m^2} - m + 2m - 2 = 0\\ \Leftrightarrow m\left( {m - 1} \right) + 2\left( {m - 1} \right) = 0\\ \Leftrightarrow \left( {m - 1} \right)\left( {m + 2} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}m = 1\\m = - 2\end{array} \right.\end{array}\)
Vậy \(m = 1\) hoặc \(m = - 2\).
Câu 3.
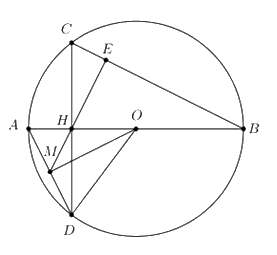
a) Bốn điểm O, M, D, H cùng thuộc một đường tròn.
Vì M là trung điểm của AD \( \Rightarrow OM \bot AD\) (quan hệ vuông góc giữa đường kính và dây cung)
\( \Rightarrow \) Điểm M, H cùng nhìn OD dưới một góc 900.
\( \Rightarrow \) Tứ giác OHMD là tứ giác nội tiếp (Tứ giác có hai đỉnh cùng nhìn một cạnh dưới các góc bằng nhau).
Vậy bốn điểm O, M, D, H cùng thuộc một đường tròn.
b) MH vuông góc với BC.
Kéo dài MH cắt BC tại E.
Xét tam giác vuông ADH có HM là đường trung tuyến ứng với cạnh huyền AD \( \Rightarrow HM = \dfrac{1}{2}AD = MD \Rightarrow \Delta MHD\) cân tại M \( \Rightarrow \widehat {MHD} = \widehat {MDH} = \widehat {ADC}\)
Lại có \(\widehat {ADC} = \widehat {ABC}\) (hai góc nội tiếp cùng chắn cung AC).
\(\widehat {MHD} = \widehat {CHE}\) (đối đỉnh)
\( \Rightarrow \widehat {CHE} = \widehat {ABC}\).
Xét tam giác vuông BCH có \(\widehat {ABC} + \widehat {HCB} = {90^0} \)
\(\Rightarrow \widehat {CHE} + \widehat {HCB} = {90^0} \)
\(\Rightarrow \Delta CHE\) vuông tại E.
\( \Rightarrow HE \bot BC\).
Vậy \(MH \bot BC\).
Câu 4
Ta có:
\(\begin{array}{l}A = \dfrac{2}{{{x^2} + {y^2}}} + \dfrac{2}{{{y^2} + {z^2}}} + \dfrac{2}{{{z^2} + {x^2}}} - \dfrac{{{x^3} + {y^3} + {z^3}}}{{2xyz}} \\= \dfrac{2}{{{x^2} + {y^2}}} + \dfrac{2}{{{y^2} + {z^2}}} + \dfrac{2}{{{z^2} + {x^2}}} - \dfrac{{{x^2}}}{{2yz}} - \dfrac{{{y^2}}}{{2xz}} - \dfrac{{{z^2}}}{{2xy}}\\ = \left( {\dfrac{2}{{{x^2} + {y^2}}} - \dfrac{{{z^2}}}{{2xy}}} \right) + \left( {\dfrac{2}{{{y^2} + {z^2}}} - \dfrac{{{x^2}}}{{2yz}}} \right) + \left( {\dfrac{2}{{{z^2} + {x^2}}} - \dfrac{{{y^2}}}{{2xz}}} \right)\end{array}\)
Áp dụng BĐT Cô si, ta có:
\(0 < 2xy \le {x^2} + {y^2},\,\,(x,\,y > 0) \)
\(\Rightarrow \dfrac{{{z^2}}}{{2xy}} \ge \dfrac{{{z^2}}}{{{x^2} + {y^2}}} \Rightarrow \dfrac{2}{{{x^2} + {y^2}}} - \dfrac{{{z^2}}}{{2xy}} \le \dfrac{2}{{{x^2} + {y^2}}} - \dfrac{{{z^2}}}{{{x^2} + {y^2}}} = \dfrac{{2 - {z^2}}}{{{x^2} + {y^2}}} = \dfrac{{{x^2} + {y^2}}}{{{x^2} + {y^2}}} = 1\)
Tương tự, \(\dfrac{2}{{{y^2} + {z^2}}} - \dfrac{{{x^2}}}{{2yz}} \le 1\), \(\dfrac{2}{{{z^2} + {x^2}}} - \dfrac{{{y^2}}}{{2xz}} \le 1\)
\(\begin{array}{l} \Rightarrow A = \left( {\dfrac{2}{{{x^2} + {y^2}}} - \dfrac{{{z^2}}}{{2xy}}} \right) + \left( {\dfrac{2}{{{y^2} + {z^2}}} - \dfrac{{{x^2}}}{{2yz}}} \right) + \left( {\dfrac{2}{{{z^2} + {x^2}}} - \dfrac{{{y^2}}}{{2xz}}} \right) \le 1 + 1 + 1 = 3\\ \Rightarrow MaxA = 3 \Leftrightarrow \left\{ \begin{array}{l}x = y = z\\{x^2} + {y^2} + {z^2} = 2\end{array} \right. \\\Leftrightarrow x = y = z = \sqrt {\dfrac{2}{3}} \end{array}\)
Đề thi vào lớp 10 môn Toán là một kỳ thi quan trọng đánh giá năng lực học tập của học sinh sau nhiều năm học tập. Việc làm quen với các dạng đề thi khác nhau, đặc biệt là các đề thi thử, là vô cùng cần thiết để chuẩn bị tốt nhất cho kỳ thi chính thức. Đề số 14 - Đề thi vào lớp 10 môn Toán mà chúng tôi cung cấp dưới đây là một ví dụ điển hình, bao gồm các câu hỏi thuộc nhiều chủ đề khác nhau, đòi hỏi học sinh phải có kiến thức vững chắc và kỹ năng giải quyết vấn đề tốt.
Đề số 14 thường bao gồm các dạng câu hỏi sau:
Phương trình bậc hai là một trong những chủ đề quan trọng thường xuyên xuất hiện trong đề thi vào lớp 10. Để giải quyết các bài toán này, học sinh cần nắm vững công thức nghiệm và các điều kiện để phương trình có nghiệm. Ví dụ, phương trình 2x2 - 5x + 2 = 0 có thể được giải bằng công thức nghiệm:
x = (-b ± √(b2 - 4ac)) / 2a
Trong trường hợp này, a = 2, b = -5, c = 2. Thay vào công thức, ta được:
x = (5 ± √((-5)2 - 4 * 2 * 2)) / (2 * 2) = (5 ± √9) / 4
Vậy, phương trình có hai nghiệm là x1 = 2 và x2 = 1/2.
Các bài toán chứng minh tính chất hình học đòi hỏi học sinh phải có kiến thức vững chắc về các định lý, tính chất, và các phương pháp chứng minh hình học. Ví dụ, chứng minh rằng hai tam giác bằng nhau theo trường hợp cạnh - góc - cạnh (c-g-c). Để chứng minh hai tam giác bằng nhau, học sinh cần chỉ ra rằng hai cạnh và góc xen giữa của hai tam giác bằng nhau.
Các bài toán về tổ hợp thường yêu cầu học sinh phải tính số lượng các cách chọn, sắp xếp các đối tượng khác nhau. Ví dụ, có bao nhiêu cách chọn 3 học sinh từ một lớp có 20 học sinh? Bài toán này có thể được giải bằng công thức tổ hợp:
C(n, k) = n! / (k! * (n - k)!)
Trong trường hợp này, n = 20 và k = 3. Thay vào công thức, ta được:
C(20, 3) = 20! / (3! * 17!) = (20 * 19 * 18) / (3 * 2 * 1) = 1140
Vậy, có 1140 cách chọn 3 học sinh từ một lớp có 20 học sinh.
Giaitoan.edu.vn cam kết cung cấp cho bạn những tài liệu ôn thi chất lượng, đáp án chi tiết và lời giải bài bản. Chúng tôi hy vọng rằng với sự hỗ trợ của chúng tôi, bạn sẽ tự tin và đạt kết quả tốt nhất trong kỳ thi vào lớp 10 môn Toán.
Hãy truy cập giaitoan.edu.vn để khám phá thêm nhiều đề thi thử và tài liệu ôn tập hữu ích khác.