Giaitoan.edu.vn xin giới thiệu bộ đề thi tuyển sinh vào lớp 10 môn Toán tỉnh Thanh Hóa năm 2018. Đây là tài liệu vô cùng quan trọng giúp các em học sinh làm quen với cấu trúc đề thi, rèn luyện kỹ năng giải toán và tự tin hơn trong kỳ thi sắp tới.
Bộ đề thi này bao gồm các đề thi chính thức của kỳ thi tuyển sinh vào lớp 10 THPT chuyên Lam Sơn và các trường THPT khác trên địa bàn tỉnh Thanh Hóa năm 2018, kèm theo đáp án chi tiết và lời giải bài tập.
Câu I: (2,0 điểm) 1) Giải phương trình
Câu I: (2,0 điểm)
1) Giải phương trình: \({x^2} + 8x + 7 = 0\)
2) Giải hệ phương trình: \(\left\{ \begin{array}{l}2x - y = - 6\\5x + y = 20\end{array} \right.\)
Câu II: (2,0 điểm)
Cho biểu thức \(A = \dfrac{{\sqrt x + 1}}{{x + 4\sqrt x + 4}}:\left( {\dfrac{x}{{x + 2\sqrt x }} + \dfrac{x}{{\sqrt x + 2}}} \right),\) với \(x > 0\)
Câu III: (2,0 điểm)
\(\sqrt {x_1^2 + 2018} - {x_1} = \sqrt {x_2^2 + 2018} + {x_2}\)
Bài IV: (3,0 điểm)
Cho đường tròn tâm \(\left( O \right)\), đường kính \(AB = 2R\). Gọi \({d_1};{d_2}\) lần lượt là các tiếp tuyến của đường tròn \(\left( O \right)\) tại A và B, I là trung điểm của đoạn thẳng OA, E là điểm thay đổi trên đường tròn \(\left( O \right)\) sao cho E không trùng với A và B. Đường thẳng d đi qua E và vuông góc với đường thẳng EI cắt \({d_1};{d_2}\) lần lượt tại M, N.
Câu V: (1,0 điểm)
Cho \(a,b,c\) là các số thực dương thỏa mãn: \(a + b + c = 1\) . Chứng minh \(\dfrac{1}{{{a^2} + {b^2} + {c^2}}} + \dfrac{1}{{abc}} \ge 30.\)
Câu I: (2,0 điểm)
1) Giải phương trình: \({x^2} + 8x + 7 = 0\)
2) Giải hệ phương trình: \(\left\{ \begin{array}{l}2x - y = - 6\\5x + y = 20\end{array} \right.\)
Câu II: (2,0 điểm)
Cho biểu thức \(A = \dfrac{{\sqrt x + 1}}{{x + 4\sqrt x + 4}}:\left( {\dfrac{x}{{x + 2\sqrt x }} + \dfrac{x}{{\sqrt x + 2}}} \right),\) với \(x > 0\)
Câu III: (2,0 điểm)
\(\sqrt {x_1^2 + 2018} - {x_1} = \sqrt {x_2^2 + 2018} + {x_2}\)
Bài IV: (3,0 điểm)
Cho đường tròn tâm \(\left( O \right)\), đường kính \(AB = 2R\). Gọi \({d_1};{d_2}\) lần lượt là các tiếp tuyến của đường tròn \(\left( O \right)\) tại A và B, I là trung điểm của đoạn thẳng OA, E là điểm thay đổi trên đường tròn \(\left( O \right)\) sao cho E không trùng với A và B. Đường thẳng d đi qua E và vuông góc với đường thẳng EI cắt \({d_1};{d_2}\) lần lượt tại M, N.
Câu V: (1,0 điểm)
Cho \(a,b,c\) là các số thực dương thỏa mãn: \(a + b + c = 1\) . Chứng minh \(\dfrac{1}{{{a^2} + {b^2} + {c^2}}} + \dfrac{1}{{abc}} \ge 30.\)
Câu I.
Phương pháp:
1) Giải phương trình bậc hai 1 ẩn sử dụng công thức nhanh có: \(a - b + c = 0\) . Khi đó phương trình luôn có một nghiệm là: \(x = - 1\) và nghiệm còn lại là: \(x = - \dfrac{c}{a}\)
2) giải hệ phương trình bằng phương pháp thế hoặc cộng đại số.
Cách giải:
1) Giải phương trình: \({x^2} + 8x + 7 = 0\)
Ta có: \(a - b + c = 1 - 8 + 7 = 0\) nên phương trình đã cho luôn có một nghiệm là \(x = - 1\) và nghiệm còn lại là: \(x = - \dfrac{c}{a} = - 7\)
Vậy tập nghiệm của phương trình là \(S = \left\{ { - 1; - 7} \right\}\).
2) Giải hệ phương trình: \(\left\{ \begin{array}{l}2x - y = - 6\\5x + y = 20\end{array} \right.\)
\(\left\{ \begin{array}{l}2x - y = - 6\\5x + y = 20\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}7x = 14\\y = 20 - 5x\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 20 - 5.2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 10\end{array} \right.\)
Vậy hệ phương trình đã cho có nghiệm là: \(\left( {x;y} \right) = \left( {2;10} \right)\)
Câu II.
Phương pháp:
1. Phân tích mẫu thành nhân tử sau đó quy đồng các mẫu thức rồi rút gọn.
2. Cho \(A \ge \dfrac{1}{{3\sqrt x }}\) sau đó tìm x và đối chiếu với điều kiện rồi kết luận.
Cách giải:
Cho biểu thức \(A = \dfrac{{\sqrt x + 1}}{{x + 4\sqrt x + 4}}:\left( {\dfrac{x}{{x + 2\sqrt x }} + \dfrac{x}{{\sqrt x + 2}}} \right),\) với \(x > 0\)
\(\begin{array}{l}A = \dfrac{{\sqrt x + 1}}{{x + 4\sqrt x + 4}}:\left( {\dfrac{x}{{x + 2\sqrt x }} + \dfrac{x}{{\sqrt x + 2}}} \right)\\ = \dfrac{{\sqrt x + 1}}{{{{\left( {\sqrt x + 2} \right)}^2}}}:\left( {\dfrac{x}{{\sqrt x \left( {\sqrt x + 2} \right)}} + \dfrac{x}{{\sqrt x + 2}}} \right)\\ = \dfrac{{\sqrt x + 1}}{{{{\left( {\sqrt x + 2} \right)}^2}}}:\left( {\dfrac{{\sqrt x }}{{\sqrt x + 2}} + \dfrac{x}{{\sqrt x + 2}}} \right)\\ = \dfrac{{\sqrt x + 1}}{{{{\left( {\sqrt x + 2} \right)}^2}}}.\dfrac{{\sqrt x + 2}}{{\sqrt x \left( {\sqrt x + 1} \right)}}\\ = \dfrac{1}{{\sqrt x \left( {\sqrt x + 2} \right)}}\end{array}\)
Vậy với \(x > 0\) thì \(A = \dfrac{1}{{\sqrt x \left( {\sqrt x + 2} \right)}}\)
\(\begin{array}{l}A \ge \dfrac{1}{{3\sqrt x }} \Leftrightarrow \dfrac{1}{{\sqrt x \left( {\sqrt x + 2} \right)}} \ge \dfrac{1}{{3\sqrt x }}\\ \Leftrightarrow \dfrac{{3 - \left( {\sqrt x + 2} \right)}}{{\sqrt x \left( {\sqrt x + 2} \right)}} \ge 0\\ \Leftrightarrow \dfrac{{1 - \sqrt x }}{{\sqrt x \left( {\sqrt x + 2} \right)}} \ge 0\end{array}\)
Với \(x > 0\) ta có: \(\sqrt x \left( {\sqrt x + 2} \right) > 0\) khi đó \(\dfrac{{1 - \sqrt x }}{{\sqrt x \left( {\sqrt x + 2} \right)}} \ge 0 \Leftrightarrow 1 - \sqrt x \ge 0 \Leftrightarrow x \le 1\)
Kết hợp với điều kiện ta được: \(0 < x \le 1\) thỏa mãn yêu cầu bài toán.
Câu III.
Phương pháp:
1.Hai đường thẳng \(\left( d \right):\,\,y = ax + b;\,\,\left( {d'} \right):\,\,y = a'x + b'\) song song với nhau khi và chỉ khi \(\left\{ \begin{array}{l}a = a'\\b \ne b'\end{array} \right.\) .
Đường thẳng (d’) đi qua điểm A(1;-1) tức là tọa độ điểm A thỏa mãn phương trình đường thẳng.
2.Chứng minh phương trình luôn có hai nghiệm phân biệt \({x_1},{x_2}\) với mọi m: Ta xét biệt thức \(\Delta = {b^2} - 4ac\) sau đó chứng minh cho \(\Delta > 0,\forall m\) .
Kết hợp hệ thức Viet với đầu bài để tìm được m.
Hệ thức Viet: \(\left\{ \begin{array}{l}{x_1} + {x_2} = - \dfrac{b}{a}\\{x_1}{x_2} = \dfrac{c}{a}\end{array} \right.\)
Cách giải:
Đường thẳng (d) song song với đường thẳng (d’) khi và chỉ khi: \(\left\{ \begin{array}{l}a = a'\\b \ne b'\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 2\\b \ne 3\end{array} \right.\)
Khi đó (d) trở thành: \(y = 2x + b\left( {b \ne 3} \right)\)
Đường thẳng (d’) đi qua điểm \(A\left( {1; - 1} \right)\) nên ta có:
\( - 1 = 2.1 + b \Leftrightarrow b = - 3\left( {tm} \right)\)
Vậy đường thẳng (d) cần tìm là: \(y = 2x - 3\)
\(\sqrt {x_1^2 + 2018} - {x_1} = \sqrt {x_2^2 + 2018} + {x_2}\)
Xét biệt thức \(\Delta = {\left( {m - 2} \right)^2} + 12 \ge 12 > 0,\forall m\)
Vậy phương trình \({x^2} - \left( {m - 2} \right)x - 3 = 0\) luôn có hai nghiệm phân biệt \({x_1};{x_2}\) với mọi m. Giả sử \({x_1} > {x_2}\)
Theo hệ thức Viet ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = m - 2\\{x_1}{x_2} = - 3\end{array} \right.\)
Theo đề ra ta có:
\(\begin{array}{l}\sqrt {x_1^2 + 2018} - {x_1} = \sqrt {x_2^2 + 2018} + {x_2}\\ \Leftrightarrow \sqrt {x_1^2 + 2018} - \sqrt {x_2^2 + 2018} = {x_1} + {x_2}\\ \Leftrightarrow x_1^2 + 2018 + x_2^2 + 2018 - 2\sqrt {\left( {x_1^2 + 2018} \right).\left( {x_2^2 + 2018} \right)} = x_1^2 + x_2^2 + 2{x_1}{x_2}\,\,\left( {Do\,\,{x_1} - {x_2} > 0} \right)\\ \Leftrightarrow 4036 - 2\sqrt {\left( {x_1^2 + 2018} \right).\left( {x_2^2 + 2018} \right)} = 2{x_1}{x_2}\\ \Leftrightarrow \sqrt {\left( {x_1^2 + 2018} \right).\left( {x_2^2 + 2018} \right)} = 2018 - {x_1}{x_2}\\ \Leftrightarrow \left( {x_1^2 + 2018} \right).\left( {x_2^2 + 2018} \right) = {2018^2} - 4036{x_1}{x_2} + x_1^2x_2^2\\ \Leftrightarrow x_1^2x_2^2 + 2018\left( {x_1^2 + x_2^2} \right) + {2018^2} = {2018^2} - 4036{x_1}{x_2} + x_1^2x_2^2\\ \Leftrightarrow \left[ {{{\left( {{x_1} + {x_2}} \right)}^2} - 2{x_1}{x_2}} \right] = - 2{x_1}{x_2}\\ \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} = 0\\ \Leftrightarrow {\left( {m - 2} \right)^2} = 0\\ \Leftrightarrow m = 2\end{array}\)
Vậy m = 2 thỏa mãn yêu cầu bài toán.
Bài IV.
Phương pháp:
Cách giải:
Cho đường tròn tâm \(\left( O \right)\), đường kính \(AB = 2R\). Gọi \({d_1};{d_2}\) lần lượt là các tiếp tuyến của đường tròn \(\left( O \right)\) tại A và B, I là trung điểm của đoạn thẳng OA, E là điểm thay đổi trên đường tròn \(\left( O \right)\) sao cho E không trùng với A và B. Đường thẳng d đi qua E và vuông góc với đường thẳng EI cắt \({d_1};{d_2}\) lần lượt tại M, N.
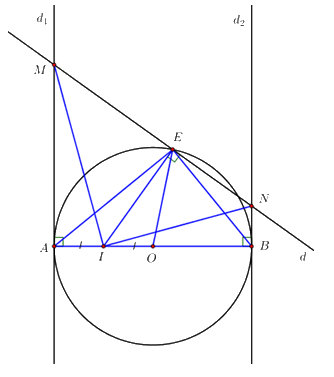
1. Chứng minh AMEI là tứ giác nội tiếp.
Ta có: MA là tiếp tuyến của (O) tại A nên \(\angle IAM = {90^0}\)
Xét tứ giác \(AMEI\) có \(\angle IAM + \angle IEM = {90^0} + {90^0} = {180^0}\)
\( \Rightarrow \) Tứ giác \(AMEI\) là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng 1800)
2. Chứng minh \(IB.NE = 3IE.NB\)
Ta có \(\angle IEA + \angle IEB = \angle AEB = {90^0}\) (góc nội tiếp chắn nửa đường tròn);
\(\angle NEB + \angle IEB = \angle NEI = {90^0}\,\,\left( {gt} \right)\);
\( \Rightarrow \angle IEA = \angle NEB\)
Xét \(\Delta IEA\) và \(\Delta NEB\) có:
\(\angle IEA = \angle NEB\,\,\left( {cmt} \right)\);
\(\angle IAE = \angle BAE = \angle NBE\) (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung BE);
\( \Rightarrow \Delta IEA \sim \Delta NEB\,\,\left( {g.g} \right) \Rightarrow \dfrac{{IE}}{{IA}} = \dfrac{{NE}}{{NB}} \Rightarrow IA.NE = IE.NB \Rightarrow 3IA.NE = 3IE.NB\)
Do I là trung điểm của OA \( \Rightarrow IA = \dfrac{1}{2}OA = \dfrac{1}{2}.\dfrac{1}{2}AB = \dfrac{1}{4}AB \Rightarrow IA = \dfrac{1}{3}IB\) hay \(IB = 3IA\).
\( \Rightarrow IB.NE = 3IE.NB\,\,\left( {dpcm} \right)\).
3. Khi điểm E thay đổi chứng minh tích \(AM.BN\) có giá trị không đổi và tìm giá trị nhỏ nhất của diện tích tam giác MNI theo R.
+) Chứng minh tích \(AM.BN\) có giá trị không đổi
Xét tứ giác \(BNEI\) có \(\angle IBN + \angle IEN = {90^0} + {90^0} = {180^0} \Rightarrow \) Tứ giác \(BNEI\) là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng 1800)
\( \Rightarrow \angle NEB = \angle NIB\) (hai góc nội tiếp cùng chắn cung NB)
Ta có \(\angle AMI = \angle AEI\) (hai góc nội tiếp cùng chắn cung AI) ;
Mà \(\angle AEI = \angle NEB\,\,\left( {cmt} \right)\)
\( \Rightarrow \angle AMI = \angle NIB\).
Xét \(\Delta AMI\) và \(\Delta BIN\) có:
\(\begin{array}{l}\angle AMI = \angle NIB\,\,\left( {cmt} \right);\\\angle MAI = \angle IBN = {90^0}\,\,\left( {gt} \right);\\ \Rightarrow \Delta AMI \sim \Delta BIN\,\,\left( {g.g} \right) \Rightarrow \dfrac{{AM}}{{BI}} = \dfrac{{AI}}{{BN}} \Rightarrow AM.BN = AI.BI\end{array}\)
Ta có \(AI = \dfrac{1}{4}AB = \dfrac{1}{4}.2R = \dfrac{R}{2};\,\,BI = \dfrac{3}{4}AB = \dfrac{3}{4}.2R = \dfrac{{3R}}{2}\)
\( \Rightarrow AM.BN = \dfrac{R}{2}.\dfrac{{3R}}{2} = \dfrac{{3{R^2}}}{4} = const\).
+) Tìm giá trị nhỏ nhất của diện tích tam giác MNI theo R.
Tứ giác BNEI là tứ giác nội tiếp (cmt) \( \Rightarrow \angle ENI = \angle EBI\) (hai góc nội tiếp cùng chắn cung EI)
Do tứ giác \(AMEI\) nội tiếp (cmt) \( \Rightarrow \angle IME = \angle IAE\) (hai góc nội tiếp cùng chắn cung IE)
\( \Rightarrow \angle ENI = \angle IME = \angle EBI + \angle IAE = {90^0}\) (\(\Delta ABE\) vuông tại E)
\( \Rightarrow \angle MIN = {90^0} \Rightarrow \Delta IMN\) vuông tại I \( \Rightarrow {S_{IMN}} = \dfrac{1}{2}IM.IN\)
Đặt \(\angle AIM = \alpha \Rightarrow \angle BNI = \alpha \,\,\left( {{0^0} < \alpha < {{90}^0}} \right)\left( {Do\,\,\Delta AMI \sim \Delta BIN} \right)\).
Xét tam giác vuông AIM có \(\cos \angle AIM = \cos \alpha = \dfrac{{AI}}{{MI}} \Rightarrow MI = \dfrac{{AI}}{{\cos \alpha }} = \dfrac{{\dfrac{R}{2}}}{{\cos \alpha }} = \dfrac{R}{{2\cos \alpha }}\)
Xét tam giác vuông BIN có : \(\sin \angle BNI = \sin \alpha = \dfrac{{BI}}{{IN}} \Rightarrow IN = \dfrac{{BI}}{{\sin \alpha }} = \dfrac{{\dfrac{{3R}}{2}}}{{\sin \alpha }} = \dfrac{{3R}}{{2\sin \alpha }}\)
\( \Rightarrow {S_{IMN}} = \dfrac{1}{2}IM.IN = \dfrac{1}{2}.\dfrac{R}{{2\cos \alpha }}.\dfrac{{3R}}{{2\sin \alpha }} = \dfrac{{3{R^2}}}{{8\sin \alpha \cos \alpha }}\)
Do \({0^0} < \alpha < {90^0} \Rightarrow \sin \alpha > 0,\,\,\cos \alpha > 0\) và \(\cos \alpha = \sqrt {1 - {{\sin }^2}\alpha } \).
\(\begin{array}{l} \Rightarrow \sin \alpha .\cos \alpha = \sin \alpha .\sqrt {1 - {{\sin }^2}\alpha } \mathop \le \limits^{Cauchy} \dfrac{{{{\sin }^2}\alpha + 1 - {{\sin }^2}\alpha }}{2} = \dfrac{1}{2}\\ \Rightarrow {S_{IMN}} \ge \dfrac{{3{R^2}}}{{8.\dfrac{1}{2}}} = \dfrac{{3{R^2}}}{4}\end{array}\)
Dấu bằng xảy ra \( \Leftrightarrow \sin \alpha = \sqrt {1 - {{\sin }^2}\alpha } \Leftrightarrow 2{\sin ^2}\alpha = 1 \Leftrightarrow \sin \alpha = \dfrac{1}{{\sqrt 2 }} \Leftrightarrow \alpha = {45^0}\)
Vậy \({S_{IMN\,\,\min }} = \dfrac{{3{R^2}}}{4} \Leftrightarrow \angle AIM = {45^0}\).
Câu V.
Ta có:
\(\begin{array}{l}\dfrac{1}{{{a^2} + {b^2} + {c^2}}} + \dfrac{1}{{abc}} = \dfrac{1}{{{a^2} + {b^2} + {c^2}}} + \dfrac{1}{{9abc}} + \dfrac{8}{{9abc}}\\ \ge \dfrac{1}{{{a^2} + {b^2} + {c^2}}} + \dfrac{1}{{3{{\left( {bc + ac + ab} \right)}^2}}} + \dfrac{8}{{9\dfrac{{{{\left( {a + b + c} \right)}^3}}}{{27}}}}\\ \ge 2\sqrt {\dfrac{1}{{{a^2} + {b^2} + {c^2}}}.\dfrac{1}{{3{{\left( {bc + ac + ab} \right)}^2}}}} + 24\\ \ge 2\sqrt {\dfrac{1}{{3\dfrac{{{{\left( {{a^2} + {b^2} + {c^2} + 2ab + 2bc + 2ac} \right)}^2}}}{{27}}}}} + 24 = 30\end{array}\)
Câu I.
Phương pháp:
1) Giải phương trình bậc hai 1 ẩn sử dụng công thức nhanh có: \(a - b + c = 0\) . Khi đó phương trình luôn có một nghiệm là: \(x = - 1\) và nghiệm còn lại là: \(x = - \dfrac{c}{a}\)
2) giải hệ phương trình bằng phương pháp thế hoặc cộng đại số.
Cách giải:
1) Giải phương trình: \({x^2} + 8x + 7 = 0\)
Ta có: \(a - b + c = 1 - 8 + 7 = 0\) nên phương trình đã cho luôn có một nghiệm là \(x = - 1\) và nghiệm còn lại là: \(x = - \dfrac{c}{a} = - 7\)
Vậy tập nghiệm của phương trình là \(S = \left\{ { - 1; - 7} \right\}\).
2) Giải hệ phương trình: \(\left\{ \begin{array}{l}2x - y = - 6\\5x + y = 20\end{array} \right.\)
\(\left\{ \begin{array}{l}2x - y = - 6\\5x + y = 20\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}7x = 14\\y = 20 - 5x\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 20 - 5.2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 10\end{array} \right.\)
Vậy hệ phương trình đã cho có nghiệm là: \(\left( {x;y} \right) = \left( {2;10} \right)\)
Câu II.
Phương pháp:
1. Phân tích mẫu thành nhân tử sau đó quy đồng các mẫu thức rồi rút gọn.
2. Cho \(A \ge \dfrac{1}{{3\sqrt x }}\) sau đó tìm x và đối chiếu với điều kiện rồi kết luận.
Cách giải:
Cho biểu thức \(A = \dfrac{{\sqrt x + 1}}{{x + 4\sqrt x + 4}}:\left( {\dfrac{x}{{x + 2\sqrt x }} + \dfrac{x}{{\sqrt x + 2}}} \right),\) với \(x > 0\)
\(\begin{array}{l}A = \dfrac{{\sqrt x + 1}}{{x + 4\sqrt x + 4}}:\left( {\dfrac{x}{{x + 2\sqrt x }} + \dfrac{x}{{\sqrt x + 2}}} \right)\\ = \dfrac{{\sqrt x + 1}}{{{{\left( {\sqrt x + 2} \right)}^2}}}:\left( {\dfrac{x}{{\sqrt x \left( {\sqrt x + 2} \right)}} + \dfrac{x}{{\sqrt x + 2}}} \right)\\ = \dfrac{{\sqrt x + 1}}{{{{\left( {\sqrt x + 2} \right)}^2}}}:\left( {\dfrac{{\sqrt x }}{{\sqrt x + 2}} + \dfrac{x}{{\sqrt x + 2}}} \right)\\ = \dfrac{{\sqrt x + 1}}{{{{\left( {\sqrt x + 2} \right)}^2}}}.\dfrac{{\sqrt x + 2}}{{\sqrt x \left( {\sqrt x + 1} \right)}}\\ = \dfrac{1}{{\sqrt x \left( {\sqrt x + 2} \right)}}\end{array}\)
Vậy với \(x > 0\) thì \(A = \dfrac{1}{{\sqrt x \left( {\sqrt x + 2} \right)}}\)
\(\begin{array}{l}A \ge \dfrac{1}{{3\sqrt x }} \Leftrightarrow \dfrac{1}{{\sqrt x \left( {\sqrt x + 2} \right)}} \ge \dfrac{1}{{3\sqrt x }}\\ \Leftrightarrow \dfrac{{3 - \left( {\sqrt x + 2} \right)}}{{\sqrt x \left( {\sqrt x + 2} \right)}} \ge 0\\ \Leftrightarrow \dfrac{{1 - \sqrt x }}{{\sqrt x \left( {\sqrt x + 2} \right)}} \ge 0\end{array}\)
Với \(x > 0\) ta có: \(\sqrt x \left( {\sqrt x + 2} \right) > 0\) khi đó \(\dfrac{{1 - \sqrt x }}{{\sqrt x \left( {\sqrt x + 2} \right)}} \ge 0 \Leftrightarrow 1 - \sqrt x \ge 0 \Leftrightarrow x \le 1\)
Kết hợp với điều kiện ta được: \(0 < x \le 1\) thỏa mãn yêu cầu bài toán.
Câu III.
Phương pháp:
1.Hai đường thẳng \(\left( d \right):\,\,y = ax + b;\,\,\left( {d'} \right):\,\,y = a'x + b'\) song song với nhau khi và chỉ khi \(\left\{ \begin{array}{l}a = a'\\b \ne b'\end{array} \right.\) .
Đường thẳng (d’) đi qua điểm A(1;-1) tức là tọa độ điểm A thỏa mãn phương trình đường thẳng.
2.Chứng minh phương trình luôn có hai nghiệm phân biệt \({x_1},{x_2}\) với mọi m: Ta xét biệt thức \(\Delta = {b^2} - 4ac\) sau đó chứng minh cho \(\Delta > 0,\forall m\) .
Kết hợp hệ thức Viet với đầu bài để tìm được m.
Hệ thức Viet: \(\left\{ \begin{array}{l}{x_1} + {x_2} = - \dfrac{b}{a}\\{x_1}{x_2} = \dfrac{c}{a}\end{array} \right.\)
Cách giải:
Đường thẳng (d) song song với đường thẳng (d’) khi và chỉ khi: \(\left\{ \begin{array}{l}a = a'\\b \ne b'\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 2\\b \ne 3\end{array} \right.\)
Khi đó (d) trở thành: \(y = 2x + b\left( {b \ne 3} \right)\)
Đường thẳng (d’) đi qua điểm \(A\left( {1; - 1} \right)\) nên ta có:
\( - 1 = 2.1 + b \Leftrightarrow b = - 3\left( {tm} \right)\)
Vậy đường thẳng (d) cần tìm là: \(y = 2x - 3\)
\(\sqrt {x_1^2 + 2018} - {x_1} = \sqrt {x_2^2 + 2018} + {x_2}\)
Xét biệt thức \(\Delta = {\left( {m - 2} \right)^2} + 12 \ge 12 > 0,\forall m\)
Vậy phương trình \({x^2} - \left( {m - 2} \right)x - 3 = 0\) luôn có hai nghiệm phân biệt \({x_1};{x_2}\) với mọi m. Giả sử \({x_1} > {x_2}\)
Theo hệ thức Viet ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = m - 2\\{x_1}{x_2} = - 3\end{array} \right.\)
Theo đề ra ta có:
\(\begin{array}{l}\sqrt {x_1^2 + 2018} - {x_1} = \sqrt {x_2^2 + 2018} + {x_2}\\ \Leftrightarrow \sqrt {x_1^2 + 2018} - \sqrt {x_2^2 + 2018} = {x_1} + {x_2}\\ \Leftrightarrow x_1^2 + 2018 + x_2^2 + 2018 - 2\sqrt {\left( {x_1^2 + 2018} \right).\left( {x_2^2 + 2018} \right)} = x_1^2 + x_2^2 + 2{x_1}{x_2}\,\,\left( {Do\,\,{x_1} - {x_2} > 0} \right)\\ \Leftrightarrow 4036 - 2\sqrt {\left( {x_1^2 + 2018} \right).\left( {x_2^2 + 2018} \right)} = 2{x_1}{x_2}\\ \Leftrightarrow \sqrt {\left( {x_1^2 + 2018} \right).\left( {x_2^2 + 2018} \right)} = 2018 - {x_1}{x_2}\\ \Leftrightarrow \left( {x_1^2 + 2018} \right).\left( {x_2^2 + 2018} \right) = {2018^2} - 4036{x_1}{x_2} + x_1^2x_2^2\\ \Leftrightarrow x_1^2x_2^2 + 2018\left( {x_1^2 + x_2^2} \right) + {2018^2} = {2018^2} - 4036{x_1}{x_2} + x_1^2x_2^2\\ \Leftrightarrow \left[ {{{\left( {{x_1} + {x_2}} \right)}^2} - 2{x_1}{x_2}} \right] = - 2{x_1}{x_2}\\ \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} = 0\\ \Leftrightarrow {\left( {m - 2} \right)^2} = 0\\ \Leftrightarrow m = 2\end{array}\)
Vậy m = 2 thỏa mãn yêu cầu bài toán.
Bài IV.
Phương pháp:
Cách giải:
Cho đường tròn tâm \(\left( O \right)\), đường kính \(AB = 2R\). Gọi \({d_1};{d_2}\) lần lượt là các tiếp tuyến của đường tròn \(\left( O \right)\) tại A và B, I là trung điểm của đoạn thẳng OA, E là điểm thay đổi trên đường tròn \(\left( O \right)\) sao cho E không trùng với A và B. Đường thẳng d đi qua E và vuông góc với đường thẳng EI cắt \({d_1};{d_2}\) lần lượt tại M, N.
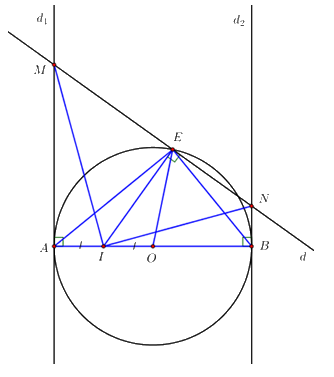
1. Chứng minh AMEI là tứ giác nội tiếp.
Ta có: MA là tiếp tuyến của (O) tại A nên \(\angle IAM = {90^0}\)
Xét tứ giác \(AMEI\) có \(\angle IAM + \angle IEM = {90^0} + {90^0} = {180^0}\)
\( \Rightarrow \) Tứ giác \(AMEI\) là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng 1800)
2. Chứng minh \(IB.NE = 3IE.NB\)
Ta có \(\angle IEA + \angle IEB = \angle AEB = {90^0}\) (góc nội tiếp chắn nửa đường tròn);
\(\angle NEB + \angle IEB = \angle NEI = {90^0}\,\,\left( {gt} \right)\);
\( \Rightarrow \angle IEA = \angle NEB\)
Xét \(\Delta IEA\) và \(\Delta NEB\) có:
\(\angle IEA = \angle NEB\,\,\left( {cmt} \right)\);
\(\angle IAE = \angle BAE = \angle NBE\) (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung BE);
\( \Rightarrow \Delta IEA \sim \Delta NEB\,\,\left( {g.g} \right) \Rightarrow \dfrac{{IE}}{{IA}} = \dfrac{{NE}}{{NB}} \Rightarrow IA.NE = IE.NB \Rightarrow 3IA.NE = 3IE.NB\)
Do I là trung điểm của OA \( \Rightarrow IA = \dfrac{1}{2}OA = \dfrac{1}{2}.\dfrac{1}{2}AB = \dfrac{1}{4}AB \Rightarrow IA = \dfrac{1}{3}IB\) hay \(IB = 3IA\).
\( \Rightarrow IB.NE = 3IE.NB\,\,\left( {dpcm} \right)\).
3. Khi điểm E thay đổi chứng minh tích \(AM.BN\) có giá trị không đổi và tìm giá trị nhỏ nhất của diện tích tam giác MNI theo R.
+) Chứng minh tích \(AM.BN\) có giá trị không đổi
Xét tứ giác \(BNEI\) có \(\angle IBN + \angle IEN = {90^0} + {90^0} = {180^0} \Rightarrow \) Tứ giác \(BNEI\) là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng 1800)
\( \Rightarrow \angle NEB = \angle NIB\) (hai góc nội tiếp cùng chắn cung NB)
Ta có \(\angle AMI = \angle AEI\) (hai góc nội tiếp cùng chắn cung AI) ;
Mà \(\angle AEI = \angle NEB\,\,\left( {cmt} \right)\)
\( \Rightarrow \angle AMI = \angle NIB\).
Xét \(\Delta AMI\) và \(\Delta BIN\) có:
\(\begin{array}{l}\angle AMI = \angle NIB\,\,\left( {cmt} \right);\\\angle MAI = \angle IBN = {90^0}\,\,\left( {gt} \right);\\ \Rightarrow \Delta AMI \sim \Delta BIN\,\,\left( {g.g} \right) \Rightarrow \dfrac{{AM}}{{BI}} = \dfrac{{AI}}{{BN}} \Rightarrow AM.BN = AI.BI\end{array}\)
Ta có \(AI = \dfrac{1}{4}AB = \dfrac{1}{4}.2R = \dfrac{R}{2};\,\,BI = \dfrac{3}{4}AB = \dfrac{3}{4}.2R = \dfrac{{3R}}{2}\)
\( \Rightarrow AM.BN = \dfrac{R}{2}.\dfrac{{3R}}{2} = \dfrac{{3{R^2}}}{4} = const\).
+) Tìm giá trị nhỏ nhất của diện tích tam giác MNI theo R.
Tứ giác BNEI là tứ giác nội tiếp (cmt) \( \Rightarrow \angle ENI = \angle EBI\) (hai góc nội tiếp cùng chắn cung EI)
Do tứ giác \(AMEI\) nội tiếp (cmt) \( \Rightarrow \angle IME = \angle IAE\) (hai góc nội tiếp cùng chắn cung IE)
\( \Rightarrow \angle ENI = \angle IME = \angle EBI + \angle IAE = {90^0}\) (\(\Delta ABE\) vuông tại E)
\( \Rightarrow \angle MIN = {90^0} \Rightarrow \Delta IMN\) vuông tại I \( \Rightarrow {S_{IMN}} = \dfrac{1}{2}IM.IN\)
Đặt \(\angle AIM = \alpha \Rightarrow \angle BNI = \alpha \,\,\left( {{0^0} < \alpha < {{90}^0}} \right)\left( {Do\,\,\Delta AMI \sim \Delta BIN} \right)\).
Xét tam giác vuông AIM có \(\cos \angle AIM = \cos \alpha = \dfrac{{AI}}{{MI}} \Rightarrow MI = \dfrac{{AI}}{{\cos \alpha }} = \dfrac{{\dfrac{R}{2}}}{{\cos \alpha }} = \dfrac{R}{{2\cos \alpha }}\)
Xét tam giác vuông BIN có : \(\sin \angle BNI = \sin \alpha = \dfrac{{BI}}{{IN}} \Rightarrow IN = \dfrac{{BI}}{{\sin \alpha }} = \dfrac{{\dfrac{{3R}}{2}}}{{\sin \alpha }} = \dfrac{{3R}}{{2\sin \alpha }}\)
\( \Rightarrow {S_{IMN}} = \dfrac{1}{2}IM.IN = \dfrac{1}{2}.\dfrac{R}{{2\cos \alpha }}.\dfrac{{3R}}{{2\sin \alpha }} = \dfrac{{3{R^2}}}{{8\sin \alpha \cos \alpha }}\)
Do \({0^0} < \alpha < {90^0} \Rightarrow \sin \alpha > 0,\,\,\cos \alpha > 0\) và \(\cos \alpha = \sqrt {1 - {{\sin }^2}\alpha } \).
\(\begin{array}{l} \Rightarrow \sin \alpha .\cos \alpha = \sin \alpha .\sqrt {1 - {{\sin }^2}\alpha } \mathop \le \limits^{Cauchy} \dfrac{{{{\sin }^2}\alpha + 1 - {{\sin }^2}\alpha }}{2} = \dfrac{1}{2}\\ \Rightarrow {S_{IMN}} \ge \dfrac{{3{R^2}}}{{8.\dfrac{1}{2}}} = \dfrac{{3{R^2}}}{4}\end{array}\)
Dấu bằng xảy ra \( \Leftrightarrow \sin \alpha = \sqrt {1 - {{\sin }^2}\alpha } \Leftrightarrow 2{\sin ^2}\alpha = 1 \Leftrightarrow \sin \alpha = \dfrac{1}{{\sqrt 2 }} \Leftrightarrow \alpha = {45^0}\)
Vậy \({S_{IMN\,\,\min }} = \dfrac{{3{R^2}}}{4} \Leftrightarrow \angle AIM = {45^0}\).
Câu V.
Ta có:
\(\begin{array}{l}\dfrac{1}{{{a^2} + {b^2} + {c^2}}} + \dfrac{1}{{abc}} = \dfrac{1}{{{a^2} + {b^2} + {c^2}}} + \dfrac{1}{{9abc}} + \dfrac{8}{{9abc}}\\ \ge \dfrac{1}{{{a^2} + {b^2} + {c^2}}} + \dfrac{1}{{3{{\left( {bc + ac + ab} \right)}^2}}} + \dfrac{8}{{9\dfrac{{{{\left( {a + b + c} \right)}^3}}}{{27}}}}\\ \ge 2\sqrt {\dfrac{1}{{{a^2} + {b^2} + {c^2}}}.\dfrac{1}{{3{{\left( {bc + ac + ab} \right)}^2}}}} + 24\\ \ge 2\sqrt {\dfrac{1}{{3\dfrac{{{{\left( {{a^2} + {b^2} + {c^2} + 2ab + 2bc + 2ac} \right)}^2}}}{{27}}}}} + 24 = 30\end{array}\)
Kỳ thi tuyển sinh vào lớp 10 môn Toán Thanh Hóa luôn được đánh giá là một kỳ thi quan trọng, đòi hỏi học sinh phải có sự chuẩn bị kỹ lưỡng. Đề thi thường bao gồm các dạng bài tập khác nhau, từ đại số, hình học đến số học và các bài toán thực tế. Việc nắm vững kiến thức cơ bản, rèn luyện kỹ năng giải toán và làm quen với các dạng đề thi là yếu tố then chốt để đạt kết quả tốt.
Đề thi vào 10 môn Toán Thanh Hóa năm 2018 thường có cấu trúc tương đối ổn định qua các năm. Thông thường, đề thi sẽ bao gồm các phần sau:
Trong đề thi vào 10 môn Toán Thanh Hóa năm 2018, các em học sinh thường gặp các dạng bài tập sau:
Để giải tốt đề thi vào 10 môn Toán Thanh Hóa năm 2018, các em học sinh cần lưu ý những điều sau:
Việc luyện tập với đề thi vào 10 môn Toán Thanh Hóa năm 2018 là một bước chuẩn bị quan trọng cho kỳ thi. Nó giúp các em học sinh:
Giaitoan.edu.vn là một website chuyên cung cấp các tài liệu luyện thi toán online chất lượng cao, bao gồm đề thi, đáp án, lời giải chi tiết và các bài giảng video. Chúng tôi cam kết mang đến cho các em học sinh những tài liệu tốt nhất để chuẩn bị cho kỳ thi vào 10 môn Toán Thanh Hóa năm 2018.
Ngoài việc luyện tập với đề thi, các em học sinh cũng nên chú trọng đến việc học lý thuyết, làm bài tập thường xuyên và tham gia các khóa học luyện thi để nâng cao kiến thức và kỹ năng. Chúc các em học sinh đạt kết quả tốt nhất trong kỳ thi vào 10 môn Toán Thanh Hóa năm 2018!
| Năm | Link đề thi |
|---|---|
| 2018 | [Link đến đề thi 2018 trên giaitoan.edu.vn] |